Numpy中Meshgrid函数介绍及2种应用场景
近期在好几个地方都看到meshgrid的使用,虽然之前也注意到meshgrid的用法。
但总觉得印象不深刻,不是太了解meshgrid的应用场景。
所以,本文将进一步介绍Numpy中meshgrid的用法。
Meshgrid函数的基本用法
在Numpy的官方文章里,meshgrid函数的英文描述也显得文绉绉的,理解起来有些难度。
可以这么理解,meshgrid函数用两个坐标轴上的点在平面上画网格。
用法:
[X,Y]=meshgrid(x,y)
[X,Y]=meshgrid(x)与[X,Y]=meshgrid(x,x)是等同的
[X,Y,Z]=meshgrid(x,y,z)生成三维数组,可用来计算三变量的函数和绘制三维立体图
这里,主要以[X,Y]=meshgrid(x,y)为例,来对该函数进行介绍。
[X,Y] = meshgrid(x,y) 将向量x和y定义的区域转换成矩阵X和Y,其中矩阵X的行向量是向量x的简单复制,而矩阵Y的列向量是向量y的简单复制(注:下面代码中X和Y均是数组,在文中统一称为矩阵了)。
假设x是长度为m的向量,y是长度为n的向量,则最终生成的矩阵X和Y的维度都是 n*m (注意不是m*n)。
文字描述可能不是太好理解,下面通过代码演示下:
加载数据
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
m, n = (5, 3)
x = np.linspace(0, 1, m)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(x,y)
查看向量x和向量y
x
out:
array([ 0. , 0.25, 0.5 , 0.75, 1. ])
y
out:
array([ 0. , 0.5, 1. ])
查看矩阵X和矩阵Y
X
out:
array([[ 0. , 0.25, 0.5 , 0.75, 1. ],
[ 0. , 0.25, 0.5 , 0.75, 1. ],
[ 0. , 0.25, 0.5 , 0.75, 1. ]])
Y
out:
array([[ 0. , 0. , 0. , 0. , 0. ],
[ 0.5, 0.5, 0.5, 0.5, 0.5],
[ 1. , 1. , 1. , 1. , 1. ]])
查看矩阵对应的维度
X.shape
out:
(3, 5)
Y.shape
out:
(3, 5)
meshgrid函数的运行过程,可以通过下面的示意图来加深理解:
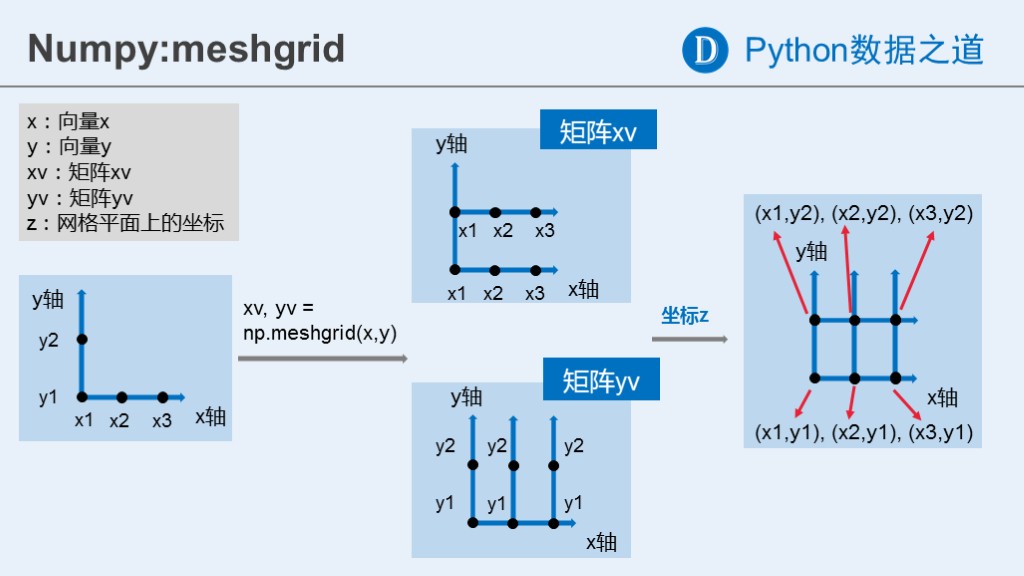

再者,也可以通过在matplotlib中进行可视化,来查看函数运行后得到的网格化数据的结果
plt.plot(X, Y, marker='.', color='blue', linestyle='none')
plt.show()

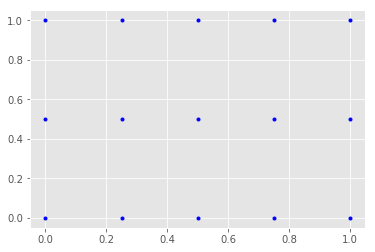
当然,我们也可以获得网格平面上坐标点的数据,如下:
z = [i for i in zip(X.flat,Y.flat)]
z
out:
[(0.0, 0.0),
(0.25, 0.0),
(0.5, 0.0),
(0.75, 0.0),
(1.0, 0.0),
(0.0, 0.5),
(0.25, 0.5),
(0.5, 0.5),
(0.75, 0.5),
(1.0, 0.5),
(0.0, 1.0),
(0.25, 1.0),
(0.5, 1.0),
(0.75, 1.0),
(1.0, 1.0)]
Meshgrid函数的一些应用场景
Meshgrid函数常用的场景有等高线绘制及机器学习中SVC超平面的绘制(二维场景下)。
分别图示如下:
(1)等高线


(2)SVC中超平面的绘制:
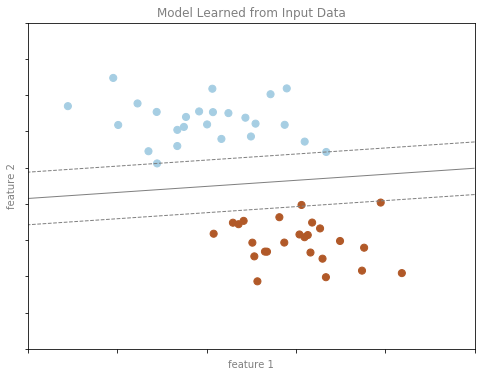
关于场景(1)和场景(2),将在后续的文章里做进一步描述。
当然,可能还有些其他场景,这里就不做进一步介绍了。
如果您喜欢我的文章,欢迎关注微信公众号:Python数据之道(ID:PyDataRoad)
出处:个人微信公众号:“Python数据之道”(ID:PyDataRoad)和博客园:http://www.cnblogs.com/lemonbit/
本文版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文出处,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号