How Many Calls? UVA - 10518

U - How Many Calls?

UVA - 10518

 

题意：

询问斐波那契数f(n)调用几次，我们可以写出方程：F(n)=F(n-1)+F(n-2)+1

 

 

 

 

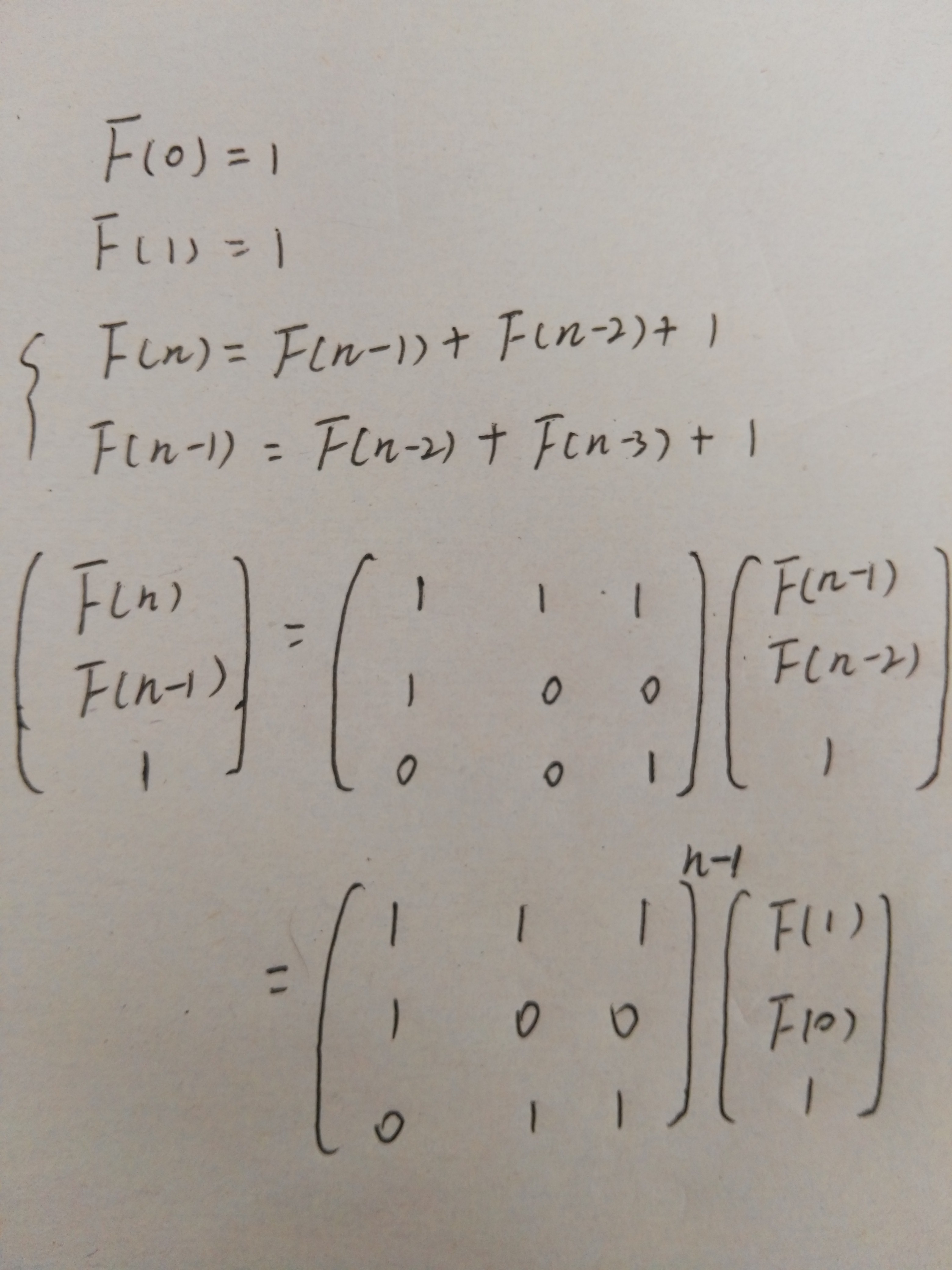
代码如下：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;

typedef long long ll;
ll MOD;
struct Matrix{
    ll matrix[3][3];
};
int n;//矩阵的阶数
void init(Matrix &res)
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
            res.matrix[i][j]=0;
        res.matrix[i][i]=1;
    }
}
Matrix multiplicative(Matrix a,Matrix b)
{
    Matrix res;
    memset(res.matrix,0,sizeof(res.matrix));
    for(int i = 0 ; i < n ; i++)
        for(int j = 0 ; j < n ; j++)
            for(int k = 0 ; k < n ; k++)
                res.matrix[i][j] = (res.matrix[i][j]+a.matrix[i][k]%MOD*b.matrix[k][j]%MOD+MOD)%MOD;
    return res;
}
Matrix pow(Matrix mx,ll m)
{
    Matrix res,base=mx;
    init(res); //初始为单位矩阵，即除主对角线都是1外，其他都是0
    while(m)
    {
        if(m&1)
            res=multiplicative(res,base);
        base=multiplicative(base,base);
        m>>=1;
    }
    return res;
}
int main()
{
    ll b;
    int cont=0;
    while(~scanf("%lld%lld",&b,&MOD)&&(b||MOD))
    {
        if(b==0||b==1)
            printf("Case %d: %lld %lld %lld\n",++cont,b,MOD,(ll)1%MOD);
        else
        {
            n=3;
            Matrix base={
                1,1,1,
                1,0,0,
                0,0,1
            };
            base=pow(base,b-1);
            printf("Case %d: %lld %lld %lld\n",++cont,b,MOD,(ll)(base.matrix[0][0]+base.matrix[0][1]+base.matrix[0][2])%MOD);
        }
    }
    return 0;
}