啥是树♤

●引入

你所认识的树可能是这样的

然后我们可以进行抽象

 

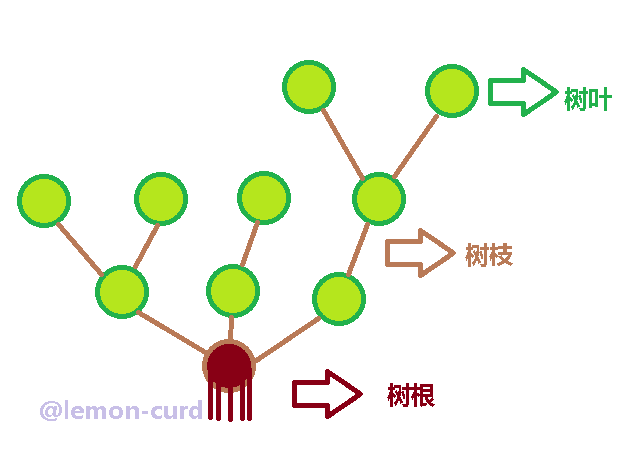
再将它倒过来，惊喜的发现，wow一棵信息学的树出现了【鼓掌】

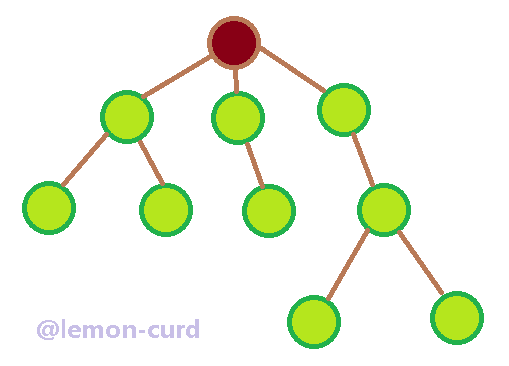
那为啥要有这样的结构呢？或许你应该在哪里见过它，比如在学习英语的时候有一节是学习亲人的——father，mother，sister等，旁边就有一个人物关系的图，就像这样

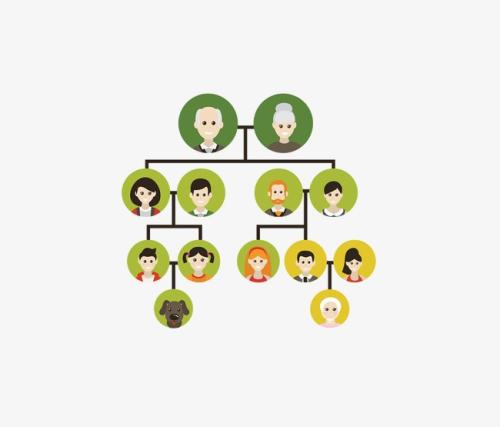
所以……树就是用来解决像家谱、行政组织机构等都是非线性的数据结构

●树的定义

接着刚才的图我们来细细了解一下树的定义：

一棵树是由n(n>0)个元素组成的有限集合，其中：

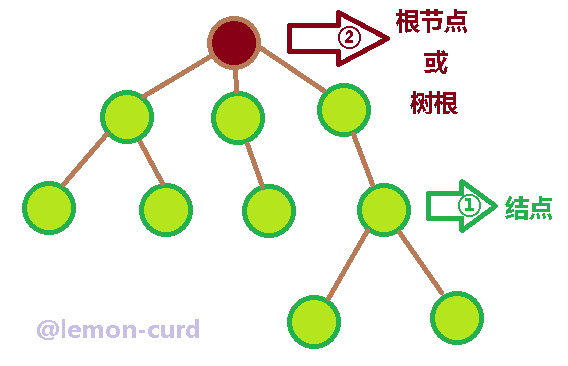
①每个元素称为结点

②有一个特定的结点，称为根节点或树根

酱酱解读：①、②如图

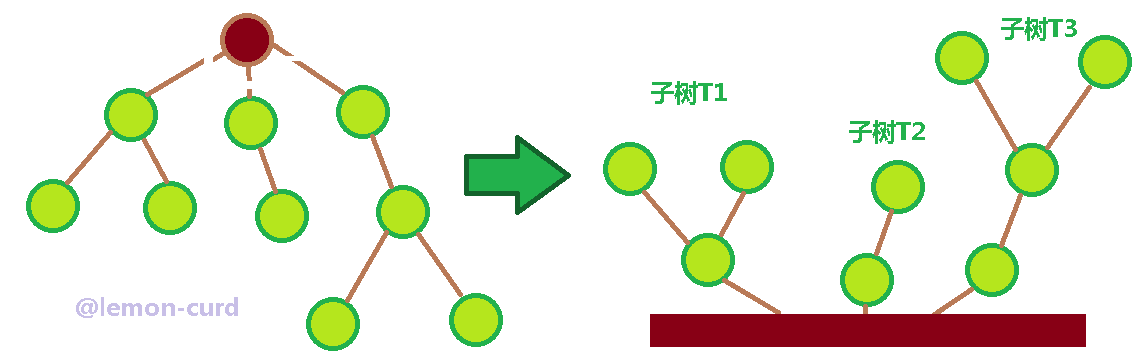
③除根节点外，其余结点能分成m(m>=0)个互不相交的有限集合T0，T1，T2,……，其中的每个子集又是一棵树，这些集合称为这棵树的子树。

酱酱解读：大概意思就是说，这棵树十分顽强，你能把它的树枝砍断插在地上它还能长，但是因为毕竟它们是由树根上生长出来的，也就相当于它的儿子，就称之为这棵树的子树

如图（当然不止这么点子树，篇章有限，理解了子树是啥就好）

 ●树的基本概念

A、树是递归定义的；
B、一棵树中至少有1个结点。这个结点就是根结点，它没有前驱，其余每个结点都有唯一的一个前驱结点。每个结点可以有0或多个后继结点。因此树虽然是非线性结构，但也是有序结构。至于前驱后继结点是哪个，还要看树的遍历方法，我们将在后面讨论；

酱酱解答B：如图

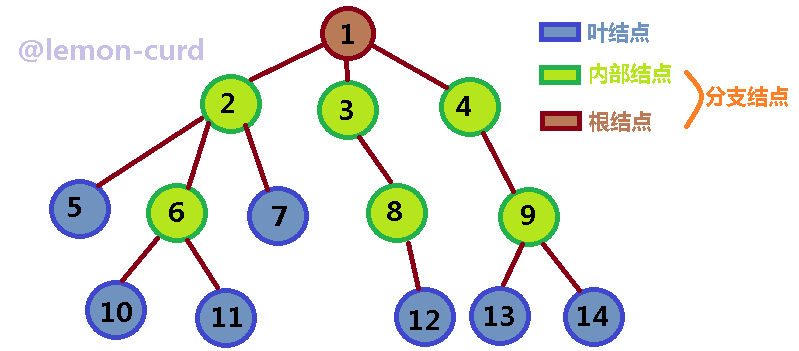
C、一个结点的子树个数，称为这个结点的度；度为0的结点称为叶结点；度不为0的结点称为分支结点；根以外的分支结点又称为内部结点；树中各结点的度的最大值称为这棵树的度。

D、在用图形表示的树型结构中，对两个用线段（称为树枝）连接的相关联的结点，称上端结点为下端结点的父结点，称下端结点为上端结点的子结点。称同一个父结点的多个子结点为兄弟结点。称从根结点到某个子结点所经过的所有结点为这个子结点的祖先。

酱酱解读：

①结点的度：可以理解为一个圈圈长出枝条的条数，举个栗子：1的度为3，4的度为1,9的度为2

②叶结点：垫底的那个可怜的球球，具体请看图与图例

③分支结点：有分支的结点，除了垫底的球球，具体请看图与图例

④内部结点：包裹在根结点和叶结点中间的结点，也就是内部，去掉爸爸和垫底的球球，具体请看图与图例

⑤树的度：孩子最多的那个球球的孩子个数，举个栗子：图中的那棵树中孩子最多的为1和2，它们的孩子数都为3，那么这棵树就以它们为荣，这棵树的度就为3

⑥父结点与子结点：emm……我jiong得好像不用说了，举个栗子：1是2、3、4的父结点，相反的2、3、4是1 的子结点；9是13、14的父结点，13、14是9的子结点

⑦兄弟结点：这个也是顾名思义，举个栗子：如图2、3、4就是兄弟结点，5、6、7也是兄弟结点

⑧结点的祖先：就相当于在很久很久以前有个猿猴叫小A，经过一代又一代，到了现在有了小B，那小A就是小B的祖先啦，举个栗子：9是13、14的祖先，2是5、6、7、10、11的祖先

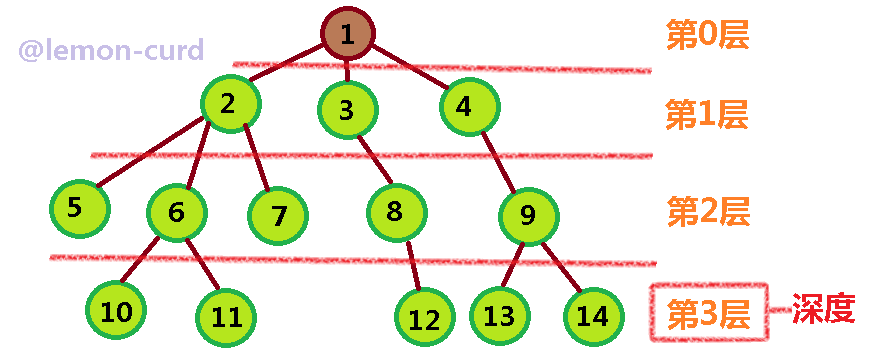
E.定义一棵树的根结点的层次为0，其它结点的层次等于它的父结点层次加1。一棵树中所有的结点的层次的最大值称为树的深度。

酱酱解读：如图

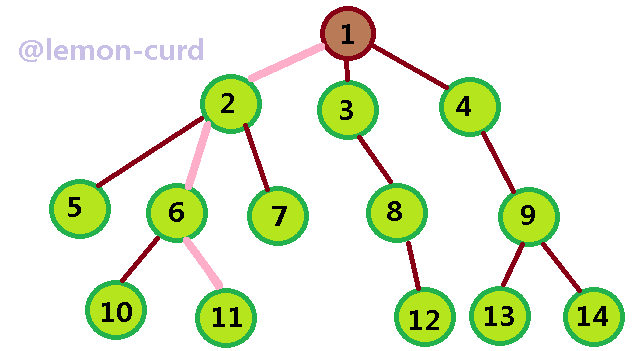
F.对于树中任意两个不同的结点，如果从一个结点出发，自上而下沿着树中连着结点的线段能到达另一结点，称它们之间存在着一条路径。可用路径所经过的结点序列表示路径，路径的长度等于路径上的结点个数减1。注意，不同子树上的结点之间不存在路径，从根结点出发，到树中的其余结点一定存在着一条路径。

酱酱解读：

路径：数一下树枝的条数就行啦，举个例子：如图，从1到11之间有3条树枝，那路径的长度就为3

G.森林是m(m>=0)棵互不相交的树的集合。

附上一张可爱的图图，感受大自然的清新与美好~

然后完美地结束这章的笔记啦~~~【by-lemon-curd】