算法模型进阶
-
贝叶斯模型
-
SVM模型
-
K均值聚类
-
DBSCAN聚类
-
GBDT模型
详细
-
贝叶斯模型
流程概述:通过已知类别的训练数据集,首先计算样本的先验概率,然后利用贝叶斯概率公式测算未知类别的样本属于各个类别的后验概率,最后将最大后验概率所对应的类别作为样本的预测值。

贝叶斯模型具有三种分类器(可以理解为计算方式)
1、高斯贝叶斯分类器
适用于自变量为连续的数值类型的情况
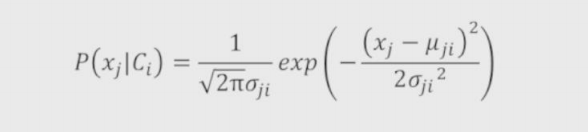

案例



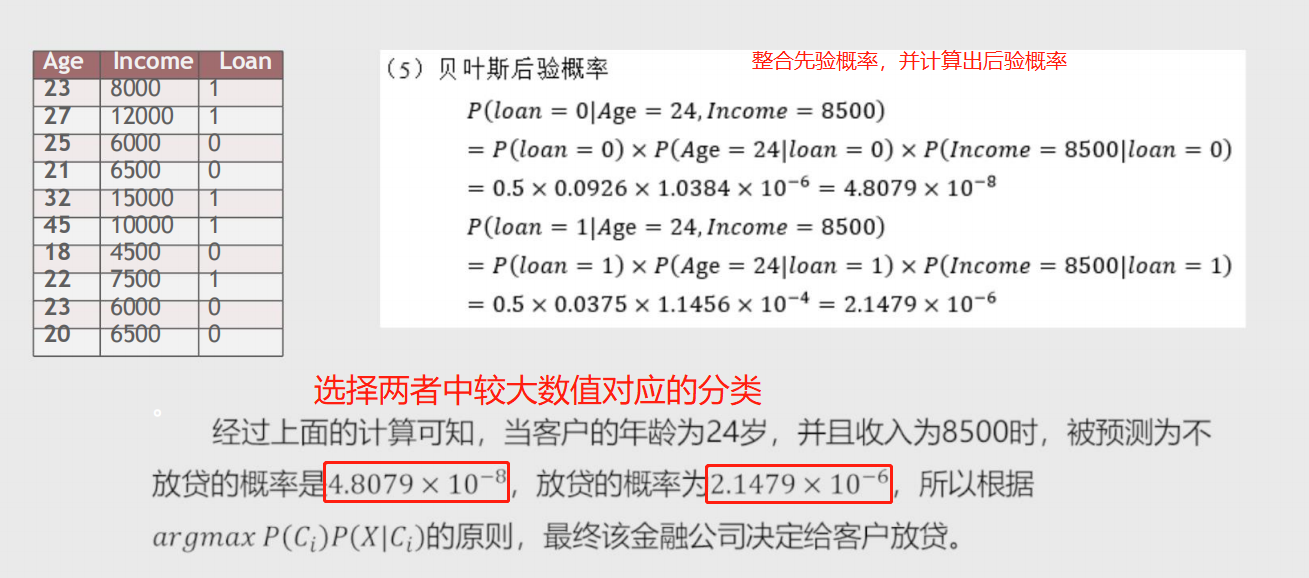
实战—皮肤识别

# 导入第三方包 import pandas as pd # 读入数据 skin = pd.read_excel(r'Skin_Segment.xlsx') skin # 设置正例和负例 skin.y = skin.y.map({2:0,1:1}) # 设置一个映射关系,将2映射成0 skin.y.value_counts() # 导入第三方模块 from sklearn import model_selection from sklearn import naive_bayes # 样本拆分 X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y,test_size = 0.25, random_state=1234) # 调用高斯朴素贝叶斯分类器的“类” gnb = naive_bayes.GaussianNB() # 模型拟合 gnb.fit(X_train, y_train) # 模型在测试数据集上的预测 gnb_pred = gnb.predict(X_test) # 各类别的预测数量 pd.Series(gnb_pred).value_counts() # 导入第三方包 from sklearn import metrics import matplotlib.pyplot as plt import seaborn as sns # 构建混淆矩阵 cm = pd.crosstab(gnb_pred,y_test) # 绘制混淆矩阵图 sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') # 去除x轴和y轴标签 plt.xlabel('Real') plt.ylabel('Predict') # 显示图形 plt.show() print('模型的准确率为:\n',metrics.accuracy_score(y_test, gnb_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, gnb_pred)) # 计算正例的预测概率,用于生成ROC曲线的数据 y_score = gnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
2、多项式贝叶斯分类器
适用于自变量为离散型变量的情况,即非数字类型


案例

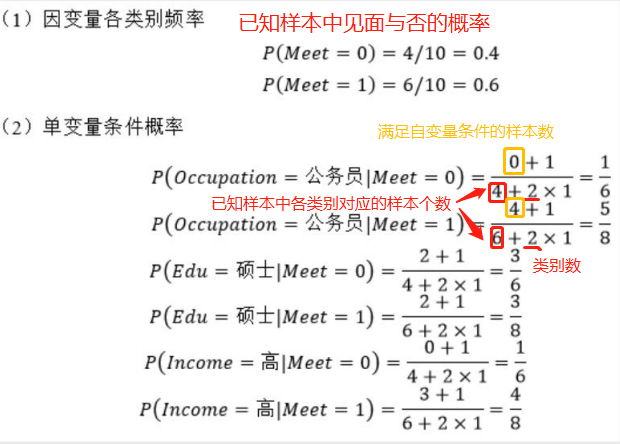

实战—毒蘑菇识别
# 导入第三方包 import pandas as pd # 读取数据 mushrooms = pd.read_csv(r'mushrooms.csv') # 数据的前5行 mushrooms.head() ################################################### # 将字符型数据作因子化处理,将其转换为整数型数据 columns = mushrooms.columns[1:] for column in columns: mushrooms[column] = pd.factorize(mushrooms[column])[0] mushrooms.head() ###################################################



from sklearn import naive_bayes from sklearn import metrics from sklearn import model_selection import seaborn as sns import matplotlib.pyplot as plt # 将数据集拆分为训练集合测试集 Predictors = mushrooms.columns[1:] X_train,X_test,y_train,y_test = model_selection.train_test_split(mushrooms[Predictors], mushrooms['type'],test_size = 0.25, random_state = 10) # 构建多项式贝叶斯分类器的“类” mnb = naive_bayes.MultinomialNB() # 基于训练数据集的拟合 mnb.fit(X_train, y_train) # 基于测试数据集的预测 mnb_pred = mnb.predict(X_test) # 构建混淆矩阵 cm = pd.crosstab(mnb_pred,y_test) # 绘制混淆矩阵图 sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') # 去除x轴和y轴标签 plt.xlabel('Real') plt.ylabel('Predict') # 显示图形 plt.show() # 模型的预测准确率 print('模型的准确率为:\n',metrics.accuracy_score(y_test, mnb_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, mnb_pred)) from sklearn import metrics # 计算正例的预测概率,用于生成ROC曲线的数据 y_score = mnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'edible':0,'poisonous':1}), y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
3、伯努利贝叶斯分类器
适用于自变量为二元值的情况


案例



实战—买家评论倾向分析

import pandas as pd # 读入评论数据 evaluation = pd.read_excel(r'Contents.xlsx',sheet_name=0) # 查看数据前10行 evaluation.head(10) # 运用正则表达式,将评论中的数字和英文去除 evaluation.Content = evaluation.Content.str.replace('[0-9a-zA-Z]','') evaluation.head() # !pip3 install jieba # !pip install jieba # 导入第三方包 import jieba # 加载自定义词库 jieba.load_userdict(r'all_words.txt') # 读入停止词 with open(r'mystopwords.txt', encoding='UTF-8') as words: stop_words = [i.strip() for i in words.readlines()] # 构造切词的自定义函数,并在切词过程中删除停止词 def cut_word(sentence): words = [i for i in jieba.lcut(sentence) if i not in stop_words] # 切完的词用空格隔开 result = ' '.join(words) return(result) # 对评论内容进行批量切词 words = evaluation.Content.apply(cut_word) # 前5行内容的切词效果 words[:5] # 导入第三方包 from sklearn.feature_extraction.text import CountVectorizer # 计算每个词在各评论内容中的次数,并将稀疏度为99%以上的词删除 counts = CountVectorizer(min_df = 0.01) # 文档词条矩阵 dtm_counts = counts.fit_transform(words).toarray() # 矩阵的列名称 columns = counts.get_feature_names() # 将矩阵转换为数据框--即X变量 X = pd.DataFrame(dtm_counts, columns=columns) # 情感标签变量 y = evaluation.Type X.head() from sklearn import model_selection from sklearn import naive_bayes from sklearn import metrics import matplotlib.pyplot as plt import seaborn as sns # 将数据集拆分为训练集和测试集 X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state=1) # 构建伯努利贝叶斯分类器 bnb = naive_bayes.BernoulliNB() # 模型在训练数据集上的拟合 bnb.fit(X_train,y_train) # 模型在测试数据集上的预测 bnb_pred = bnb.predict(X_test) # 构建混淆矩阵 cm = pd.crosstab(bnb_pred,y_test) # 绘制混淆矩阵图 sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') # 去除x轴和y轴标签 plt.xlabel('Real') plt.ylabel('Predict') # 显示图形 plt.show() # 模型的预测准确率 print('模型的准确率为:\n',metrics.accuracy_score(y_test, bnb_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, bnb_pred)) # 计算正例Positive所对应的概率,用于生成ROC曲线的数据 y_score = bnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'Negative':0,'Positive':1}), y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
-
SVM模型

超平面的概念:将样本点划分为不同的类别(表现形式:点、线、面)。
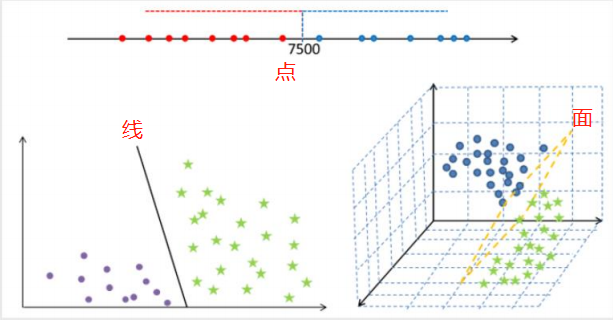
# 求超平面最优解的流程 1.随机选择一条直线 2.分别计算两边距离该直线最短的点对应的距离,取更小值 3.向左右两边划分该距离的分隔带 4.依次执行上述步骤,得出的最宽分隔带对应的直线就是最优解
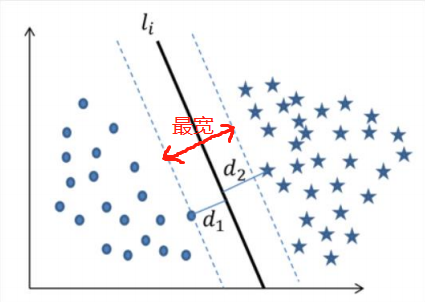
分割带
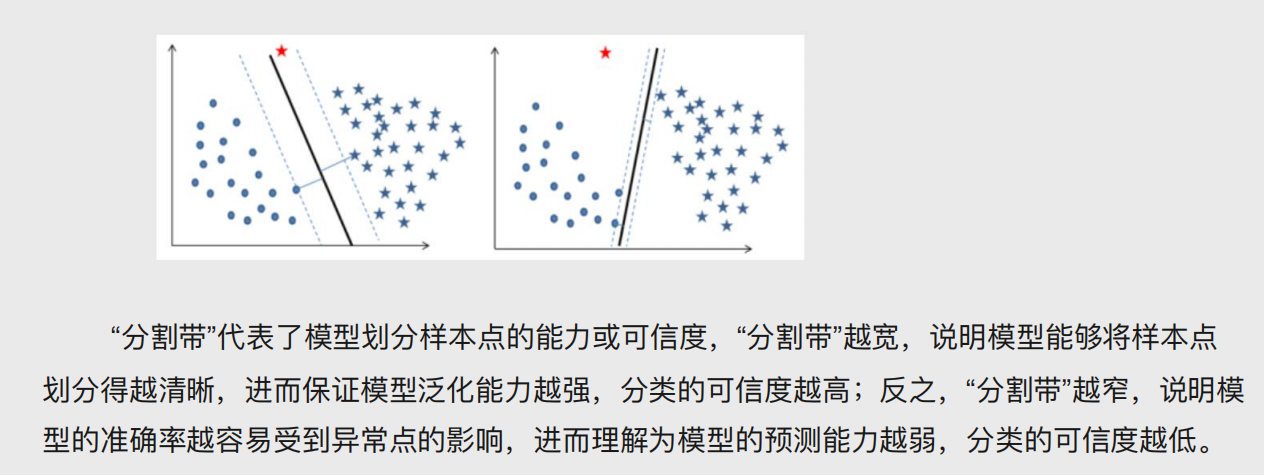

线性可分与非线性可分
# 线性可分 可以用一条直线划分类别 # 非线性可分 无法用一条直线划分类别,需要提升一个维度处理
核函数

实战—手写体字母的识别

# 导入第三方模块 from sklearn import svm import pandas as pd from sklearn import model_selection from sklearn import metrics # 读取外部数据 letters = pd.read_csv(r'letterdata.csv') # 数据前5行 letters.head() # 将数据拆分为训练集和测试集 predictors = letters.columns[1:] X_train,X_test,y_train,y_test = model_selection.train_test_split(letters[predictors], letters.letter,test_size = 0.25, random_state = 1234) # 选择线性可分SVM模型 linear_svc = svm.LinearSVC() # 模型在训练数据集上的拟合 linear_svc.fit(X_train,y_train) # 模型在测试集上的预测 pred_linear_svc = linear_svc.predict(X_test) # 模型的预测准确率 metrics.accuracy_score(y_test, pred_linear_svc) # 0.5802 # 选择非线性SVM模型 nolinear_svc = svm.SVC(kernel='rbf') # 模型在训练数据集上的拟合 nolinear_svc.fit(X_train,y_train) # 模型在测试集上的预测 pred_svc = nolinear_svc.predict(X_test) # 模型的预测准确率 metrics.accuracy_score(y_test,pred_svc) # 0.9734
-
K均值聚类
K值求解方法
1、拐点法
计算不同K值下类别中的离差平方和
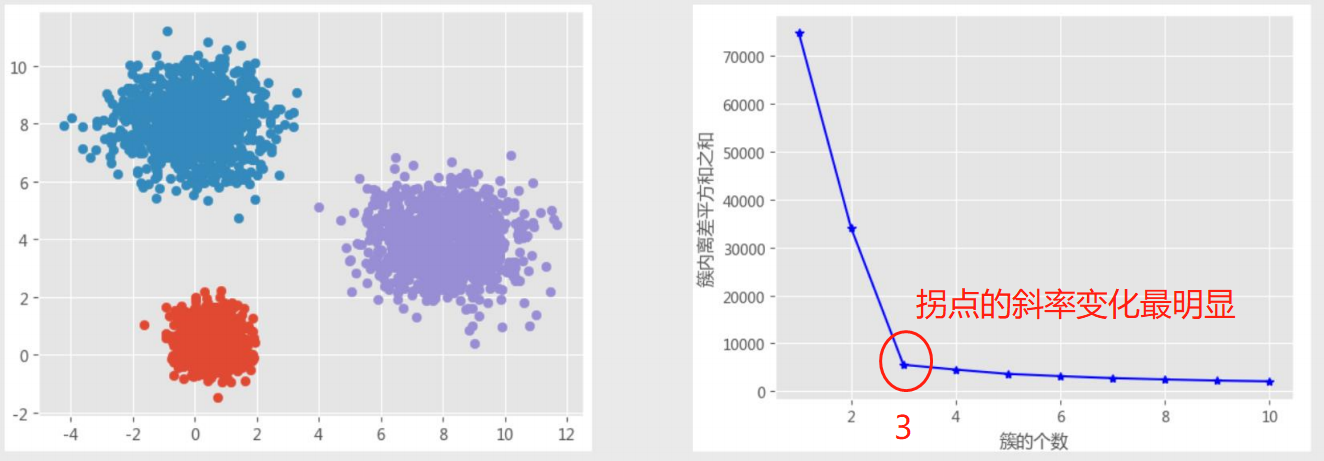

2、轮廓系数法
计算轮廓系数
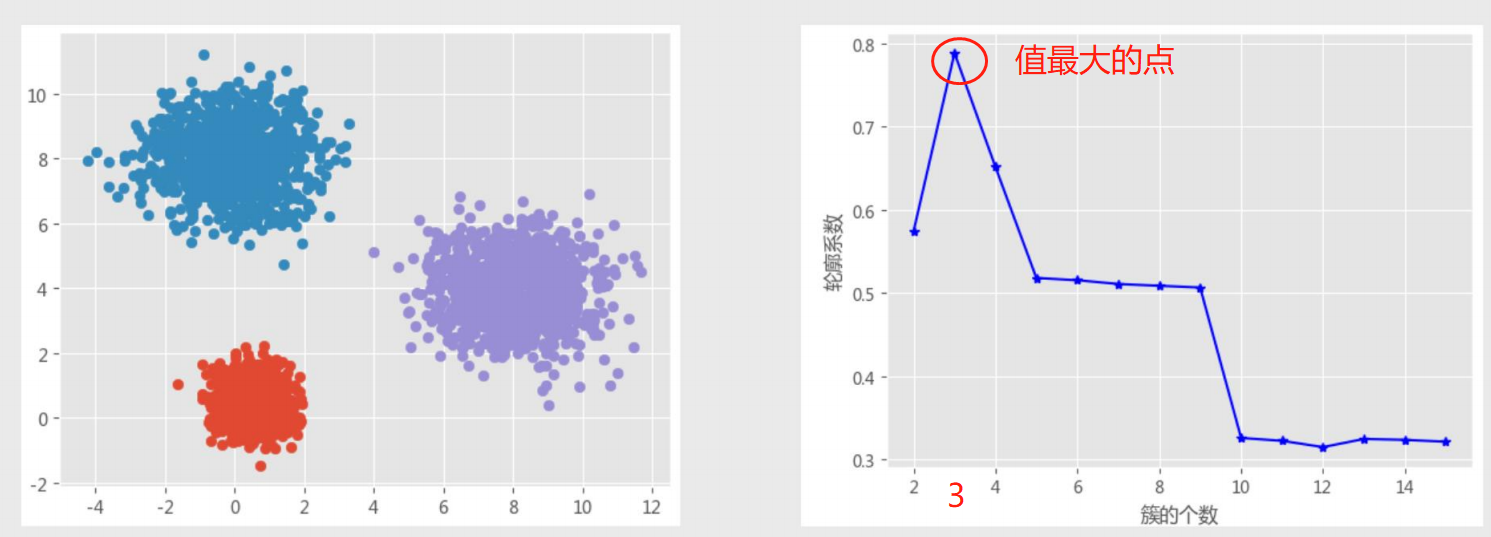


实战1—iris聚类(已知k值)

# 导入第三方包 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn import metrics # 读取iris数据集 iris = pd.read_csv(r'iris.csv') # 查看数据集的前几行 iris.head() # 提取出用于建模的数据集X X = iris.drop(labels = 'Species', axis = 1) # 构建Kmeans模型 kmeans = KMeans(n_clusters = 3) kmeans.fit(X) # 聚类结果标签 X['cluster'] = kmeans.labels_ # 各类频数统计 X.cluster.value_counts() # 导入第三方模块 import seaborn as sns # 三个簇的簇中心 centers = kmeans.cluster_centers_ # 绘制聚类效果的散点图 sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'], data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False) plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130) plt.xlabel('花瓣长度') plt.ylabel('花瓣宽度') # 图形显示 plt.show() # 增加一个辅助列,将不同的花种映射到0,1,2三种值,目的方便后面图形的对比 iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2}) # 绘制原始数据三个类别的散点图 sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'], fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False) plt.xlabel('花瓣长度') plt.ylabel('花瓣宽度') # 图形显示 plt.show()
实战2—NBA球员聚类(未知K值)

# 读取球员数据 players = pd.read_csv(r'players.csv') players.head() # 绘制得分与命中率的散点图 sns.lmplot(x = '得分', y = '命中率', data = players,fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'}) plt.show() from sklearn import preprocessing # 数据标准化处理 X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']]) # 将数组转换为数据框 X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率']) # 使用拐点法选择最佳的K值 k_SSE(X, 15) # 使用轮廓系数选择最佳的K值 k_silhouette(X, 10) # 将球员数据集聚为3类 kmeans = KMeans(n_clusters = 3) kmeans.fit(X) # 将聚类结果标签插入到数据集players中 players['cluster'] = kmeans.labels_ # 构建空列表,用于存储三个簇的簇中心 centers = [] for i in players.cluster.unique(): centers.append(players.ix[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean()) # 将列表转换为数组,便于后面的索引取数 centers = np.array(centers) # 绘制散点图 sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'], fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False) # 添加簇中心 plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180) plt.xlabel('得分') plt.ylabel('命中率') # 图形显示 plt.show()
-
DBSCAN聚类
Kmeans聚类存在两个致命缺点
⼀、聚类效果容易受到异常样本点的影响。
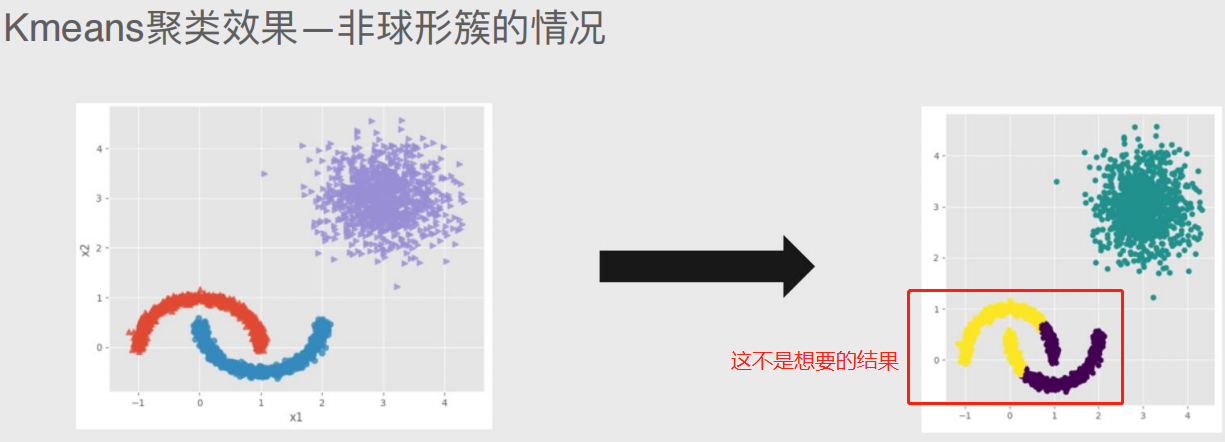
⼆、该算法⽆法准确地将⾮球形样本进⾏合理的聚类。

基于密度的聚类则可以解决⾮球形簇的问题,“密度”可以理解为样本点的紧密程度,如果在指定的半径领域内,实际样本量超过给定的最⼩样本量阈值,则认为是密度⾼的对象,就可以聚成⼀个簇。
# 核心对象 内部含有至少大于等于最少样本点的样本。 # 非核心对象 内部样本数小于最少样本点。 # 直接密度可达 在核心对象内部的样本点到核心对象的距离。 # 密度可达 若两个点经由多个直接密度可达链接了多个核心对象,则称该两点密度可达。
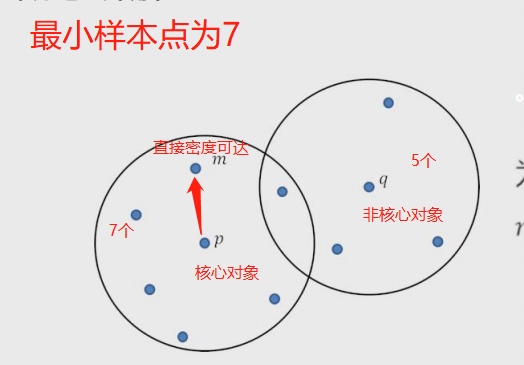
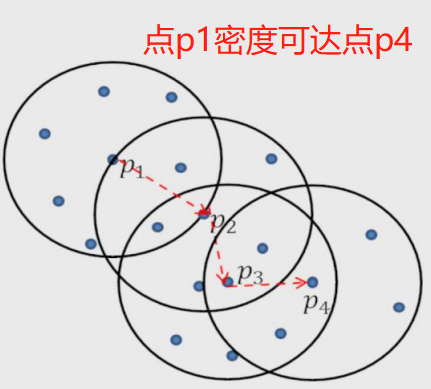
DBSCAN聚类与Kmeans聚类比较
球形簇
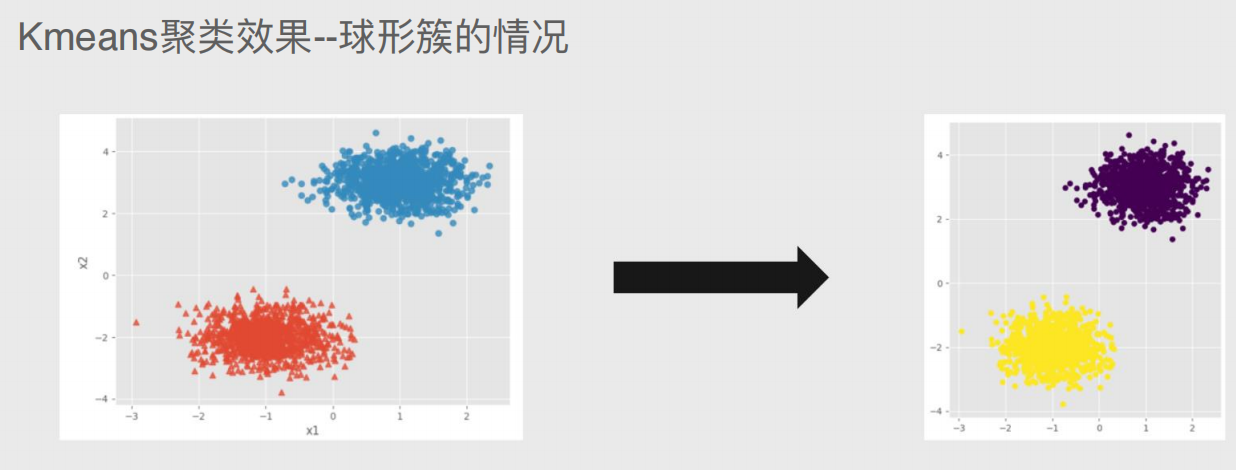
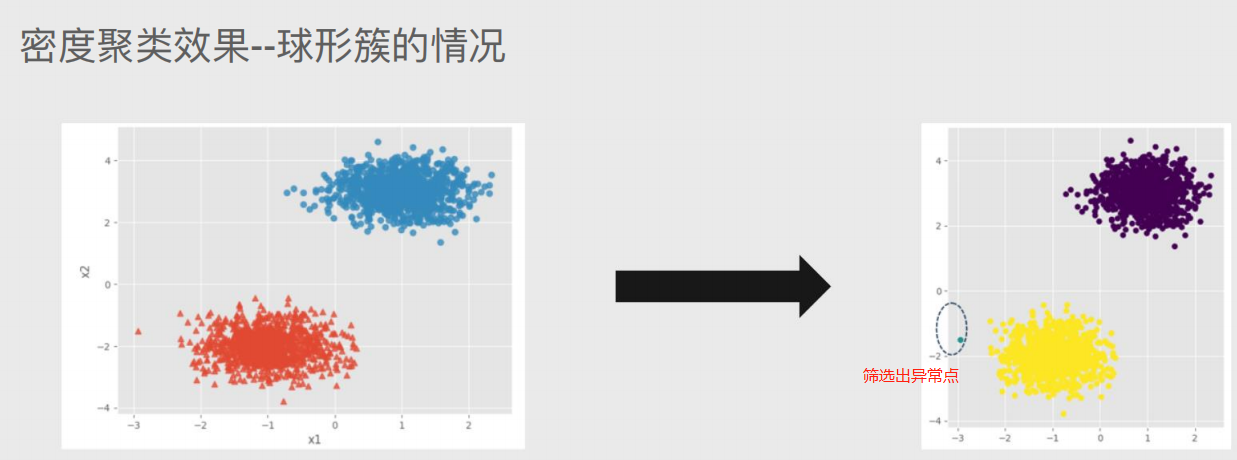
非球形簇
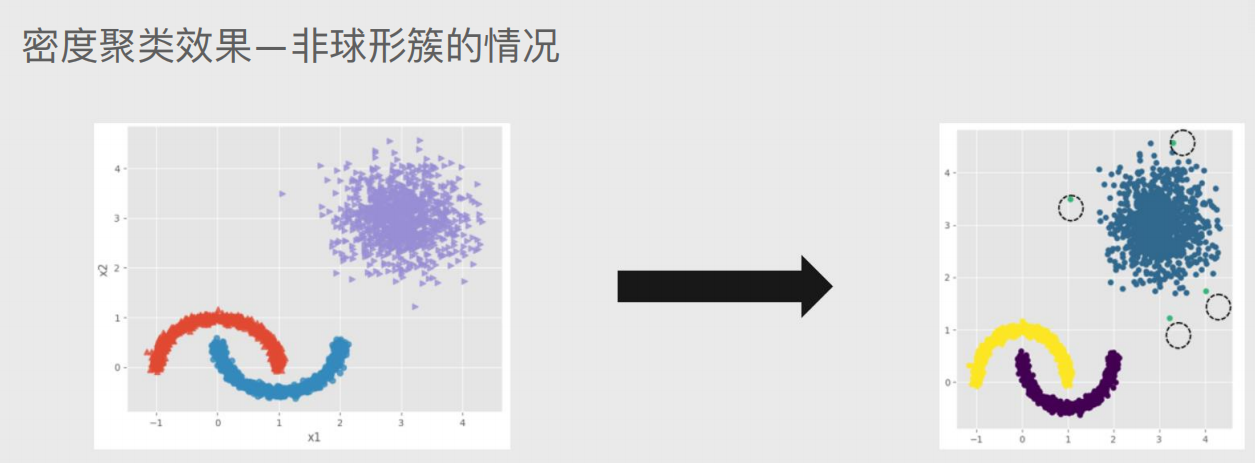
实战1

# 导入第三方模块 import pandas as pd import numpy as np from sklearn.datasets.samples_generator import make_blobs import matplotlib.pyplot as plt import seaborn as sns from sklearn import cluster # 模拟数据集 X,y = make_blobs(n_samples = 2000, centers = [[-1,-2],[1,3]], cluster_std = [0.5,0.5], random_state = 1234) # 将模拟得到的数组转换为数据框,用于绘图 plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y']) # 设置绘图风格 plt.style.use('ggplot') # 绘制散点图(用不同的形状代表不同的簇) sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'], fit_reg = False, legend = False) # 显示图形 plt.show() # 导入第三方模块 from sklearn import cluster # 构建Kmeans聚类和密度聚类 kmeans = cluster.KMeans(n_clusters=2, random_state=1234) kmeans.fit(X) dbscan = cluster.DBSCAN(eps = 0.5, min_samples = 10) dbscan.fit(X) # 将Kmeans聚类和密度聚类的簇标签添加到数据框中 plot_data['kmeans_label'] = kmeans.labels_ plot_data['dbscan_label'] = dbscan.labels_ # 绘制聚类效果图 # 设置大图框的长和高 plt.figure(figsize = (12,6)) # 设置第一个子图的布局 ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0)) # 绘制散点图 ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label) # 设置第二个子图的布局 ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1)) # 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致,通过序列的map“方法”对颜色作重映射) ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:2,1:0})) # 显示图形 plt.show() # 导入第三方模块 from sklearn.datasets.samples_generator import make_moons # 构造非球形样本点 X1,y1 = make_moons(n_samples=2000, noise = 0.05, random_state = 1234) # 构造球形样本点 X2,y2 = make_blobs(n_samples=1000, centers = [[3,3]], cluster_std = 0.5, random_state = 1234) # 将y2的值替换为2(为了避免与y1的值冲突,因为原始y1和y2中都有0这个值) y2 = np.where(y2 == 0,2,0) # 将模拟得到的数组转换为数据框,用于绘图 plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1,y1)),np.column_stack((X2,y2))]), columns = ['x1','x2','y']) # 绘制散点图(用不同的形状代表不同的簇) sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o','>'], fit_reg = False, legend = False) # 显示图形 plt.show() # 构建Kmeans聚类和密度聚类 kmeans = cluster.KMeans(n_clusters=3, random_state=1234) kmeans.fit(plot_data[['x1','x2']]) dbscan = cluster.DBSCAN(eps = 0.3, min_samples = 5) dbscan.fit(plot_data[['x1','x2']]) # 将Kmeans聚类和密度聚类的簇标签添加到数据框中 plot_data['kmeans_label'] = kmeans.labels_ plot_data['dbscan_label'] = dbscan.labels_ # 绘制聚类效果图 # 设置大图框的长和高 plt.figure(figsize = (12,6)) # 设置第一个子图的布局 ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0)) # 绘制散点图 ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label) # 设置第二个子图的布局 ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1)) # 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致,通过序列的map“方法”对颜色作重映射) ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:0,1:3,2:2})) # 显示图形 plt.show()
实战2

# 读取外部数据 Province = pd.read_excel(r'Province.xlsx') Province.head() # 绘制出生率与死亡率散点图 plt.scatter(Province.Birth_Rate, Province.Death_Rate, c = 'steelblue') # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') # 显示图形 plt.show() # 读入第三方包 from sklearn import preprocessing # 选取建模的变量 predictors = ['Birth_Rate','Death_Rate'] # 变量的标准化处理 X = preprocessing.scale(Province[predictors]) X = pd.DataFrame(X) X # 构建空列表,用于保存不同参数组合下的结果 res = [] # 迭代不同的eps值 for eps in np.arange(0.001,1,0.05): # 迭代不同的min_samples值 for min_samples in range(2,10): dbscan = cluster.DBSCAN(eps = eps, min_samples = min_samples) # 模型拟合 dbscan.fit(X) # 统计各参数组合下的聚类个数(-1表示异常点) n_clusters = len([i for i in set(dbscan.labels_) if i != -1]) # 异常点的个数 outliners = np.sum(np.where(dbscan.labels_ == -1, 1,0)) # 统计每个簇的样本个数 stats = str(pd.Series([i for i in dbscan.labels_ if i != -1]).value_counts().values) res.append({'eps':eps,'min_samples':min_samples,'n_clusters':n_clusters,'outliners':outliners,'stats':stats}) # 将迭代后的结果存储到数据框中 df = pd.DataFrame(res) df # 根据条件筛选合理的参数组合 df.loc[df.n_clusters == 3, :] %matplotlib # 中文乱码和坐标轴负号的处理 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 利用上述的参数组合值,重建密度聚类算法 dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3) # 模型拟合 dbscan.fit(X) Province['dbscan_label'] = dbscan.labels_ # 绘制聚类聚类的效果散点图 sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label', data = Province, markers = ['*','d','^','o'], fit_reg = False, legend = False) # 添加省份标签 for x,y,text in zip(Province.Birth_Rate,Province.Death_Rate, Province.Province): plt.text(x+0.1,y-0.1,text, size = 8) # 添加参考线 plt.hlines(y = 5.8, xmin = Province.Birth_Rate.min(), xmax = Province.Birth_Rate.max(), linestyles = '--', colors = 'red') plt.vlines(x = 10, ymin = Province.Death_Rate.min(), ymax = Province.Death_Rate.max(), linestyles = '--', colors = 'red') # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') # 显示图形 plt.show() # 导入第三方模块 from sklearn import metrics # 构造自定义函数,用于绘制不同k值和对应轮廓系数的折线图 def k_silhouette(X, clusters): K = range(2,clusters+1) # 构建空列表,用于存储个中簇数下的轮廓系数 S = [] for k in K: kmeans = cluster.KMeans(n_clusters=k) kmeans.fit(X) labels = kmeans.labels_ # 调用字模块metrics中的silhouette_score函数,计算轮廓系数 S.append(metrics.silhouette_score(X, labels, metric='euclidean')) # 中文和负号的正常显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 设置绘图风格 plt.style.use('ggplot') # 绘制K的个数与轮廓系数的关系 plt.plot(K, S, 'b*-') plt.xlabel('簇的个数') plt.ylabel('轮廓系数') # 显示图形 plt.show() # 聚类个数的探索 k_silhouette(X, clusters = 10) # 利用Kmeans聚类 kmeans = cluster.KMeans(n_clusters = 3) # 模型拟合 kmeans.fit(X) Province['kmeans_label'] = kmeans.labels_ # 绘制Kmeans聚类的效果散点图 sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'kmeans_label', data = Province, markers = ['d','^','o'], fit_reg = False, legend = False) # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') plt.show()
-
GBDT模型
模型介绍
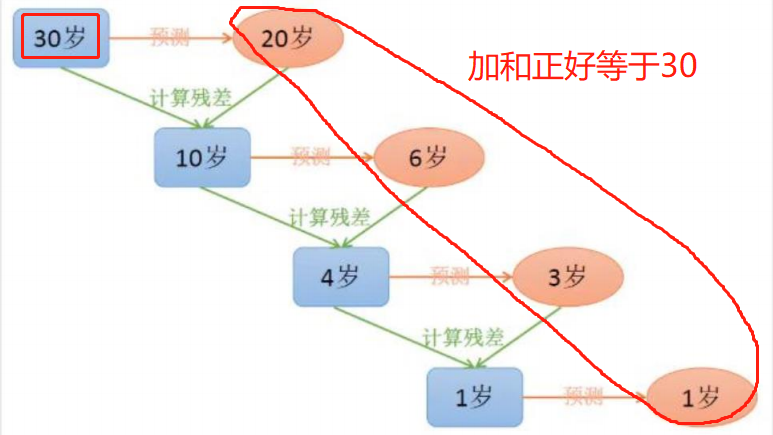
模型函数介绍


1、Adaboost算法:由多颗基础决策树组成 并且这些决策树彼此之间有先后关系(既可以解决分类问题也可以解决预测问题)。




2、SMOTE算法:通过算法将比例较少的数据样本扩大。

3、XGboost算法


-
算法模型结尾
# 有监督学习与无监督学习 1.有监督意思就是有明确需要研究的因变量Y 2.无监督意思就是没有明确需要研究的因变量Y '''算法''' 算法其实就是研究问题的解决方法 因此,算法工程师的日常工作就是在研究解决某个问题的最优方法。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号