【大一C语言】关于打印图形题的一些简单小寄巧

简单图形建模（图形打印题）简单总结

由于时间紧迫，格式啥的就不要在意了，凑合看吧

---

目录

1. 输出方法
   (1)循环数字
   (2)循环字母
   (3)printf格式控制
2. 建模方法
   (1)直接法
   (2)数组填充法
   (3)表达式法/坐标法
3. （别人的）一些模型

1.输出方法

(1)循环数字

每次移动一位：

//取余法：
num = (num + 1) % 10;//加一
num = (num - 1 + 10) % 10;//减一
//返璞归真：
if(num == 10)num = 0;
if(num == -1)num = 9;

每次移动若干位：

设st为数字起点，x为偏移量 （说白了就是st加几） ，若输出的数字只有0~9，则可以输出：

printf("%d", (st + x) % 10);

如果x可能是正的，也可能是负的，则可以写成：

printf("%d", (st + x % 10 + 10) % 10);

实在看不懂或者不带要的话写个函数

int printnum(int st, int x){
     int ans = st + x;
     while(ans < 0)ans += 10;
     while(ans > 9)ans -= 10;
     return ans;
}
//主函数：
printf("%d", printnum(st, x));
### (2)循环字母（以小写字母为例，大写字母同理）
#### 每次移动一位：
```c
ch = 'a' + (ch - 'a' + 1) % 26;//加一
ch = 'a' + (ch - 'a' - 1 + 26) % 26;//减一
//返璞归真:
if(ch == 'a' - 1)ch = 'z';
if(ch == 'z' + 1)ch = 'a';

每次移动若干位：

设st为字母起点，x为偏移量 （说白了就是st加几） ，则可以输出：

printf("%c", 'a' + ((st - 'a') + x) % 26);
printf("%c", 'a' + (((st - 'a') + x) % 26 + 26) % 26);//x可正可负

实在看不懂或者不带要的话写个函数

char printcapital(char st, int x){
     if(st >= 'a' && st <= 'z') {
           int ans = (int)st + x;//用int，以防止超出char范围
           while(ans < 'a')ans += 26;
           while(ans > 'z')ans -= 26;
           return (char)ans;
     }
     else if(st >= 'A' && st <= 'Z') {
           int ans = (int)st + x;//用int，同上
           while(ans < 'A')ans += 26;
           while(ans > 'Z')ans -= 26;
           return (char)ans;
     }
     else return st;//鬼知道你输入的啥
}
//主函数：
printf("%c", printcapital(st, x));

(3)printf格式控制（能记就记）

有时会要求一些特殊格式，比如补空格啥的，这是可以试试printf的格式控制符，详见CSDN大佬总结的:
printf()函数格式控制详解，这里推荐几个常见的要记住的（%后面的数字代表最小宽度，可以自己改，下面只是举例）：

printf("test1:%3d\n", y);//输出宽度最小为3，不足3位自动补空格，数字默认右对齐y = 20
printf("test2:%-6d%-6d\n", 5, 3);//输出宽度最小为6，不足6位自动补空格，使数字左对齐（负号代表方向，肥肠河狸）
printf("test3:%04d\n", x);输出宽度最小为4，不足4位自动补0，数字默认右对齐,x = 9;
printf("test4:%.3lf\n", d);//对于（双）浮点数，保留3位小数（四舍五入）, d = 1.234567
printf("test5:%.5lf\n", d);//对于（双）浮点数，保留5位小数,不够5位就末尾补0, d = 1.2

输出结果如下

test1: 20[回车]
test2:5  3  [回车]
test3:0009[回车]
test4:1.234[回车]
test5:1.20000[回车]

此外还有一种去掉行首空格的方法：（选看）

int i = 1;
for(i = 1; i <= 5; i++) {
     printf(" %d" + !(i - 1), i);
}//当i等于1时跳过空格（不输出前面的空格）

上面的代码等价于：

int i = 1;
for(i = 1; i <= 5; i++) {
	    if(i != 1)printf(" ");
     printf("%d", i);
	}//当i等于1时不输出前面的空格

输出：

1 2 3 4 5[回车]

2.建模方法

(1)直接法（干就完了）

适用于比较简单的图形，说白了就是用for循环、i和j，一点点做

核心步骤：

• 观察图形，确定i和j的范围（这点很重要！！！这个确定好了，思路会很清晰）
• 找特定位置，如中线，对称轴，边界等
• 利用==划线，利用>=和<=填面
• 处理符号和输出格式
• 特判0,1,2等特殊数字
  还要注意到奇偶数的问题，巧用向上和向下取整
  下面我们用例子说明：

eg:打印数字冰淇淋
输入n（n为奇数）和st，要求高度为n，循环数字，从st开始
输入样例：
5 7
输出样例：

output:
       5[回车]
     6 6 6[回车]
   7 7 7 7 7[回车]
 8 8 8 8 8 8 8[回车]
9 9 9 9 9 9 9 9 9[回车]
 0           0[回车]
   1       1[回车]
     2   2[回车]
       3[回车]

第一步，观察图形，确定范围：

可以分成上下两部分
对于上半部分，可以发现
i的范围取0到n - 1时，j的范围可以取1到n + i
下半部分对称，直接取i从n-2到0，j的范围可以不变
同时注意特判n = 1
于是就有了：（不会闹代码格式，凑合看吧）

 int n, st;
	scanf("%d %d", &n, &st);
	if(n == 1){
		printf("%d\n", st);
		return 0;
	}
 for(i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {
			//上半
		}
		printf("\n");
	}
	for(i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			//下半
		}
		printf("\n");
	}
 return 0;

第二步，找特定位置，确定输出：

找中线： i = n; （此处n为奇数）
找边界（中线两端）： n - i <= j <= n + i;是有数字分布的区域，其余为空格

第三步，利用==划线，利用>=和<=填面

上半为面，下班为线：

for( i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {

			if(j >= n - i && j <= n + i){
				//上半为面，注意是&&，此处输出数字
			}
			else {
				//否则输出空格
			}
		}
		printf("\n");//记得换行
	}
	for( i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			if(j == n - i || j == n + i){
				//下半为线，注意是||，此处输出数字
			}
			else {
				//否则输出空格
			}
		}
		printf("\n");//记得换行
	}

第四步：确定输出符号

有两种方式：

1. 计算：
   这里是循环数字，可以发现上半第i行输出（st + i） % 10
   下半第i行输出(st + 2 * (n - 1) - i) % 10
   去掉首位空格，于是就有：

for( i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {
			if(j >= n - i && j <= n + i){
				printf(" %d" + !(j - 1), (st + i) % 10);
			}
			else {
				printf("  " + !(j - 1));
			}
		}
		printf("\n");
	}
	for( i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			if(j == n - i || j == n + i){
				printf(" %d" + !(j - 1), (st + 2 * (n - 1) - i) % 10);
			}
			else {
				printf("  " + !(j - 1));
			}
		}
		printf("\n");
	}

上面的代码等价于：

for( i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {
			if(j >= n - i && j <= n + i){
				if(j != 1)printf(" ");//特判首位的空格
				printf("%d", (st + i) % 10);
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
		printf("\n");
	}
	for( i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			if(j == n - i || j == n + i){
				if(j != 1)printf(" ");
				printf("%d", (st + 2 * (n - 1) - i) % 10);
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
		printf("\n");
	}

2.单独找一个变量记录输出的数字或者字母：
核心思想是每次输出完（一行或一个）num，就有num = (num + 1) % 10;

int num = st;
	for( i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {
			if(j >= n - i && j <= n + i){
				if(j != 1)printf(" ");
				printf("%d", num);
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
       num = (num + 1) % 10;
		printf("\n");
	}
	for( i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			if(j == n - i || j == n + i){
				if(j != 1)printf(" ");
				printf("%d", num);
				
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
      num = (num + 1) % 10;
		printf("\n");
	}

至此此题完成：

#include <stdio.h>

int main(int argc, char** argv) {
	int n, st;
	scanf("%d %d", &n, &st);
	if(n == 1){
		printf("%d\n", st);
		return 0;
	}
	else;
	
	int i,j;
	int num = st;
	for( i = 0; i < n; i++) {
		for(j = 1; j <= n + i; j++) {
			if(j >= n - i && j <= n + i){
				if(j != 1)printf(" ");
				printf("%d", num);
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
		num = (num + 1) % 10;
		printf("\n");
	}
	for( i = n - 2; i >= 0; i--) {
		for(j = 1; j <= n + i; j++) {
			if(j == n - i || j == n + i){
				if(j != 1)printf(" ");
				printf("%d", num);
				
			}
			else {
				if(j != 1)printf(" ");
				printf(" ");
			}
		}
		num = (num + 1) % 10;
		printf("\n");
	}
	
	return 0;
}

(2)数组填充法

顾名思义，开一个二维数组，当成你的“画板”，在“画板”上面画图
原理很简单，想怎么画怎么画，这里简单介绍几点思路：

核心思路：

• 可以分成好几部分处理，不受顺序限制（不过有覆盖和数字顺序的情况下还是有一点点影响的）
• 计算指定的位置上的元素，同时处理好边界问题（因为是数组，所以边界问题很重要！！！）
• 对于符号、数字和字母混合的问题，可以统统采用数字储存，用一些特殊数字存符号，比如-1代表空格，-2代表*，1到26存小写字母，27到52存大写字母等等
• 对于有一定分区规律的，可以采用递归或者分治（说白了就是高级点的循环，直接用循环也可）

注意！！
有时候图形太大，数组可能需要开大一些，不然会越界
推荐把数组开到外面，在（主）函数外面定义的数组（占用静态存储空间）可以拥有更大的空间（否则可能会出现本地编译器运行不了，乐学上却可以运行的情况），同时会自动赋值为（不过保险起见还是手动赋值为>0比较好，使用int num[300][300] = {0};可以直接将整个数组初始化为0）

eg:回形数字方阵：
输入边长n，输出回形方阵
要求数据宽度为3，n <= 300
输入样例：

5[回车]

输出样例：

output:
 1  2  3  4  5[回车]
16 17 18 19  6[回车]
15 24 25 20  7[回车]
14 23 22 21  8[回车]
13 12 11 10  9[回车]

接下来我们以n等于5为例看这个画板：
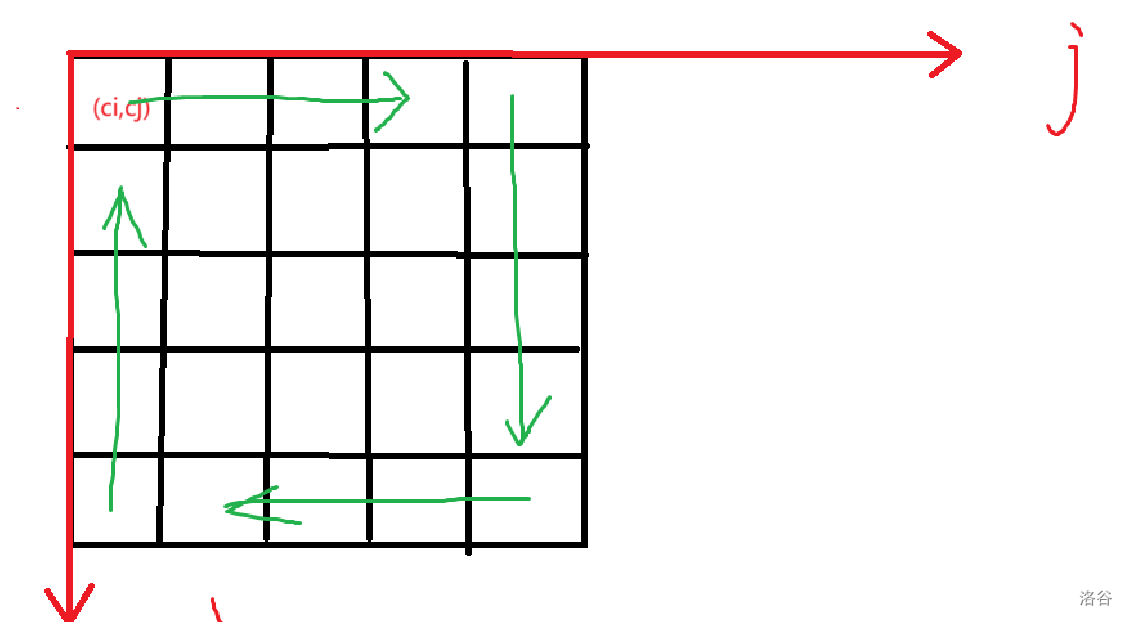
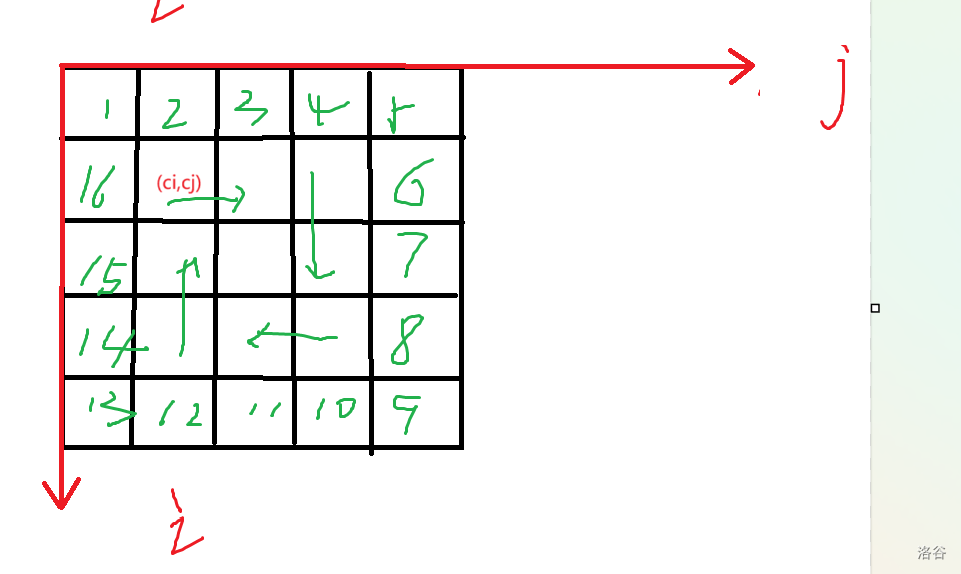
首先i - j建立坐标系（不建也行）
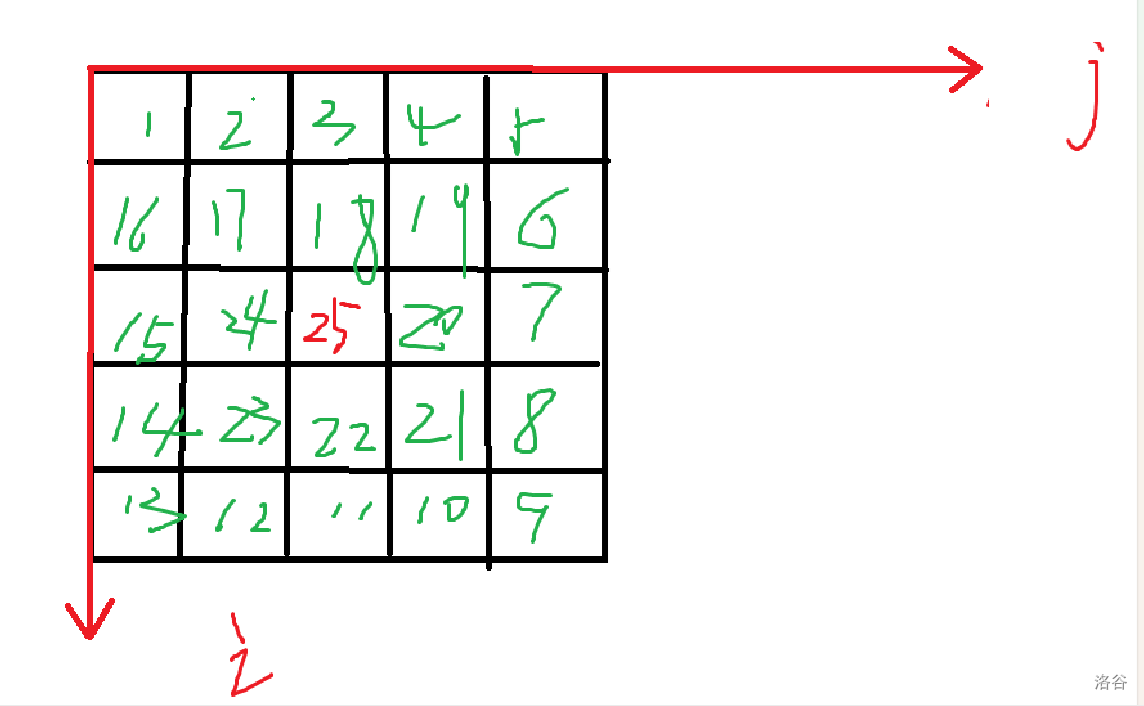
不妨按照“回”字顺序，从外到内依次填充，每一圈从(ci,cj)开始，画四条长为len的线段（如图）



最后注意奇数的时候填上中间的最后一个数字
思路很简单，没什么好说的，详情见代码

#include <stdio.h>

int ans[305][305] = {0};//记得初始化

void huixing(int n) {
	int cj = 1, ci = 1;//每一圈的左上角的点的坐标
	int len = n - 1;//每一圈要走的长度
	int num = 1;//要输出的数字
	int i, j;//当前位置
	while(len > 0) {
		i = ci, j = cj;
		//画上面的边：i保持ci不变，j加
		for(j = cj; j < cj + len; j++) {
			ans[i][j] = num++;
		}
		//画右边的边，j保持cj + len不变，i加
		for(i = ci; i < ci + len; i++) {
			ans[i][j] = num++;
		}
		//画下边的边，i保持ci + len不变，j减
		for(j = cj + len; j > cj ; j--) {
			ans[i][j] = num++;
		}
		//画左边的边，j保持cj不变，i减
		for(i = ci + len; i > ci; i--) {
			ans[i][j] = num++;
		}
		//准备下一圈
		cj ++;
		ci ++;
		len -= 2;
	}
	if(n & 1) {
		ans[(n + 1) / 2][(n + 1) / 2] = num++;
	}//若为奇数，注意中心的数！！！！
	return;
}

int main(int argc, char** argv) {
	int n, st;
	scanf("%d", &n);
	if(n == 1){
		printf("1\n");
		return 0;
	}
	else{
		huixing(n);
	}
	int i, j;
	for(i = 1; i <= n; i++) {
		for(j = 1; j <= n; j++) {
			printf("%3d", ans[i][j]);//输出宽度为3
		}
		printf("\n");
	}
	
	return 0;
}

(3)表达式法/坐标法(不想动脑子，算就完了！)

一句话：求f(i,j,n);
其实就是在直接法的基础上梳理思路，再加上亿点点计算，写成函数，便于敲代码
可以纯计算，也可以纯梳理思路
eg:
输入奇数n、图形左上角的字母，在屏幕上输出如图所示的由大写英文字母围起的图形。无论输入的字母是大写或小写，输出的字母均是大写，且字母输出是循环的，即输出2'后接着输出' 。(↙表示回车)如输入的左上>角字符不是字母或输入的数字不是奇数，输出“input error! ”

输入样例：

5 m[回车]

输出样例：

output:
MNOPQ[回车]
N P R[回车]
O Q S[回车]
P R T[回车]
QRSTU[回车]

先定义字母输出函数：

char Capital(char st, int x) {
	int ans;
   ans = (int)st + x;
	while(ans < 'A')ans += 26;
	while(ans > 'Z')ans -= 26;
	return (char)ans;
}

接下来写出f(i,j,n);
$f(i,j,n) = \begin{cases}
Capital(st, i + j) & i = 0 || i = n - 1 || j = 0 || j = n - 1 || j = n / 2 \
空格 & i, j \in \ else
\end{cases}$

其中：
$0 \le i,j < n$

于是就有代码：

#include <stdio.h>

char Capital(char st, int x) {
	int ans ;
	ans = (int)st + x;
	while(ans < 'A')ans += 26;
	while(ans > 'Z')ans -= 26;
	return (char)ans;
}

char f(int i, int j, int n, char st) {
	if(i == 0 || i == n - 1 || j == 0 || j == n - 1 || j == n / 2){
		return Capital(st, i + j);
	}
	else return ' ';
}

int main() {
	int n;
	char st;
	scanf("%d %c", &n, &st);
	
	if(n % 2 == 0) {
		printf("input error!\n");
		return 0;
	}
	else;
	
	if(st >= 'a' && st <= 'z'){
		st = st - 'a' + 'A';
	}
	else;
	
	int i, j;
	for(i = 0; i < n; i++) {
		for(j = 0; j < n; j++) {
			printf("%c", f(i, j, n, st));
		}
		printf("\n");
	}
	
	return 0;
}

3.（别人的）一些模型

再不会就看看这些：

c语言经典习题之打印10种图形图案;

---

that's all
求dalao指点

最后，
恋恋世界第一可爱！！！