实现矩阵连乘的动态规划算法
1.计算连个矩阵乘积的标准算法: //标准算法 void MatrixMultiply(int a[][MAXN], int b[][MAXN], int p, int q, int r) { int sum[MAXN][MAXN]; memset(sum, 0, sizeof(sum));
int i, j, k; //遍历矩阵a的行 for (k = 0; k < p; k++) { //遍历矩阵b的列 for (j = 0; j < r; j++) { //对应位置相乘 for (i = 0; i < q; i++) { sum[k][j] += a[k][i] * b[i][j]; } } } } 所以A、B两个矩阵相乘的计算量为p*q*r。
2. 计算连个矩阵乘积的动态规划算法: #include <stdio.h> #include <stdlib.h> #include<Windows.h>
#define MAX 100
int matrix_chain(int *p, int n, int **m, int **s) { //a[][]最小乘次数 //s[][]最小乘数时的断开点 int i,j,r,k;
for (i = 0; i < n; i++) //单一矩阵的最小乘次都置为0 { m[i][i] = 0; }
for (r = 2; r <= n; r++) //r为连乘矩阵的个数 { for (i = 0; i <= n-r; i++) //i表示连乘矩阵中的第一个 { j = i + r -1; //j表示连乘矩阵中的最后一个 m[i][j] = 99999; for (k = i; k <= j-1; k++) //在第一个与最后一个之间寻找最合适的断开点,注意,这是从i开始,即要先计算两个单独矩阵相乘的乘次 { int tmp = m[i][k] + m[k+1][j] + p[i]*p[k+1]*p[j+1]; if (tmp < m[i][j]) { m[i][j] = tmp; s[i][j] = k; } } } } return m[0][n-1]; }
void print_chain(int i, int j, char **a,int **s) { //递归的方式来把最小乘数的表达式输出
if (i == j) { printf("%s",a[i]); } else { printf("("); print_chain(i,s[i][j],a,s); print_chain(s[i][j]+1,j,a,s); printf(")"); } }
int main() { //min_part[i][j]存储的是i+1到j+1的最小乘次,因为是从0开始 //min_point[i][j]存储的是i+1到j+1之间最小乘次时的分割点 int *p, **min_part, **min_point; char **a; int n = 6,i; int ret;
p = (int *)malloc((n+1)*sizeof(int)); a = (char **)malloc(n*sizeof(char*)); min_part = (int **)malloc(n*sizeof(int *)); min_point = (int **)malloc(n*sizeof(int *));
for (i = 0; i < n; i++) { min_part[i] = (int *)malloc(n*sizeof(int)); min_point[i] = (int *)malloc(n*sizeof(int)); a[i] = (char *)malloc(n*sizeof(char)); }
p[0] = 30; //第一个矩阵的行数 p[1] = 35; //第二个矩阵的行数 p[2] = 15; //…… p[3] = 5; //…… p[4] = 10; //…… p[5] = 20; //第六个矩阵的行数 p[6] = 25; //第六个矩阵的列数
a[0] = "A1"; a[1] = "A2"; a[2] = "A3"; a[3] = "A4"; a[4] = "A5"; a[5] = "A6";
ret = matrix_chain(p,n,min_part,min_point); printf("Minest times:%d.\n",ret); print_chain(0,n-1,a,min_point); printf("\n");
free(p); free(min_part); free(min_point); free(a); system("pause");
return 0; }
3. 递归加括号的过程的运算量: //加括号的过程是递归的。 //m数组内存放矩阵链的行列信息 //m[i-1]和m[i]分别为第i个矩阵的行和列(i = 1、2、3...) int Best_Enum(int m[], int left, int right) { //只有一个矩阵时,返回计算次数0 if (left == right) { return 0; }
int min = INF; //无穷大 int i; //括号依次加在第1、2、3...n-1个矩阵后面 for (i = left; i < right; i++) { //计算出这种完全加括号方式的计算次数 int count = Best_Enum(m, left, i) + Best_Enum(m, i+1, right); count += m[left-1] * m[i] * m[right]; //选出最小的 if (count < min) { min = count; } } return min; }
4. 动态规划法和备忘录优化法程序的运算量:
//动态规划法
int m[SIZE]; //存放矩阵链的行列信息,m[i-1]和m[i]分别为第i个矩阵的行和列(i = 1、2、3...) int d[SIZE][SIZE]; //存放矩阵链计算的最优值,d[i][j]为第i个矩阵到第j个矩阵的矩阵链的最优值,i > 0
int Best_DP(int n) { //把d[i][i]置为0,1 <= i < n memset(d, 0, sizeof(d));
int len; //递归计算矩阵链的连乘最优值 //len = 1,代表矩阵链由两个矩阵构成 for (len = 1; len < n; len++) { int i, j, k; for (i = 1, j = i+len; j < n; i++, j++) { int min = INF; //无穷大 for (k = i; k < j; k++) { int count = d[i][k] + d[k+1][j] + m[i-1] * m[k] * m[j]; if (count < min) { min = count; } } d[i][j] = min; } } return d[1][n-1]; } //备忘录优化法 int memo[SIZE][SIZE];
//m数组内存放矩阵链的行列信息 //m[i-1]和m[i]分别为第i个矩阵的行和列(i = 1、2、3...) int Best_Memo(int m[], int left, int right) { //只有一个矩阵时,返回计算次数0 if (left == right) { return 0; }
int min = INF; int i; //括号依次加在第1、2、3...n-1个矩阵后面 for (i = left; i < right; i++) { //计算出这种完全加括号方式的计算次数 int count; if (memo[left][i] == 0) { memo[left][i] = Best_Memo(m, left, i); } count = memo[left][i]; if (memo[i+1][right] == 0) { memo[i+1][right] = Best_Memo(m, i+1, right); } count += memo[i+1][right]; count += m[left-1] * m[i] * m[right]; //选出最小的 if (count < min) { min = count; } } return min; }
int main(void) { int n; int c; char ch; cout<<"按对应数字选择相应方法:"<<endl; cout<<"-------------"<<endl; cout<<"1.备忘录方法"<<endl; cout<<"2.动态规划法"<<endl; cout<<"-------------"<<endl; cout<<"请输入数字:"; cin>>c; switch (c) { case 2: cout<<endl; cout<<"----------动态规划法----------"<<endl; while (scanf("%d", &n) != EOF) { int i; for (i = 0; i < n; i++) { scanf("%d", &m[i]); }
printf("%d\n", Best_DP(n)); cout<<"是否继续(y/n)?"<<endl; cin>>ch; if(ch == 'n'|ch == 'N') exit(0); }; break; case 1: cout<<endl; cout<<"----------备忘录方法----------"<<endl; while (scanf("%d", &n) != EOF) { int i; for (i = 0; i < n; i++) { scanf("%d", &m[i]); } memset(memo, 0, sizeof(memo)); printf("%d\n", Best_Memo(m, 1, n-1)); cout<<"是否继续(y/n)?"<<endl; cin>>ch; if(ch == 'n'|ch == 'N') exit(0); }; break; } return 0; } |
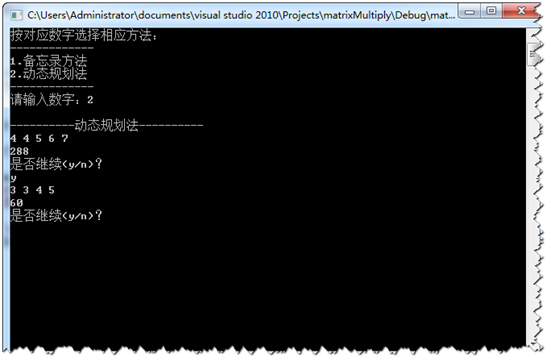
程序运行结果如下:
对于矩阵连乘的标准算法,主要计算量在三重循环,总共需要pqr次数乘; 而使用动态规划算法,在计算过程中保存已解决的子问题的答案。每个子问题只计算一次,而在后面需要时只需要检查一下,从而避免大量重复的运算。 备忘录方法与动态规划法方法虽不同但当实验数据一样时运行结果相同,证明实验中使用的两种方法都是正确的。 综上,矩阵连乘的最有次序计算问题可用自顶向下的备忘录算法或自顶向上的动态规划算法在O(n3)计算时间内求解。这两个算法都利用了子问题的重叠性质,节省了计算量,提高了算法的效率。 |





 浙公网安备 33010602011771号
浙公网安备 33010602011771号