leetcode题解之盛最多水的容器
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入:[1,8,6,2,5,4,8,3,7] 输出:49
📺视频题解
📖文字题解
方法一:双指针
说明
本题是一道经典的面试题,最优的做法是使用「双指针」。如果读者第一次看到这题,不一定能想出双指针的做法。
分析
我们先从题目中的示例开始,一步一步地解释双指针算法的过程。稍后再给出算法正确性的证明。
题目中的示例为:
[1, 8, 6, 2, 5, 4, 8, 3, 7]
^ ^
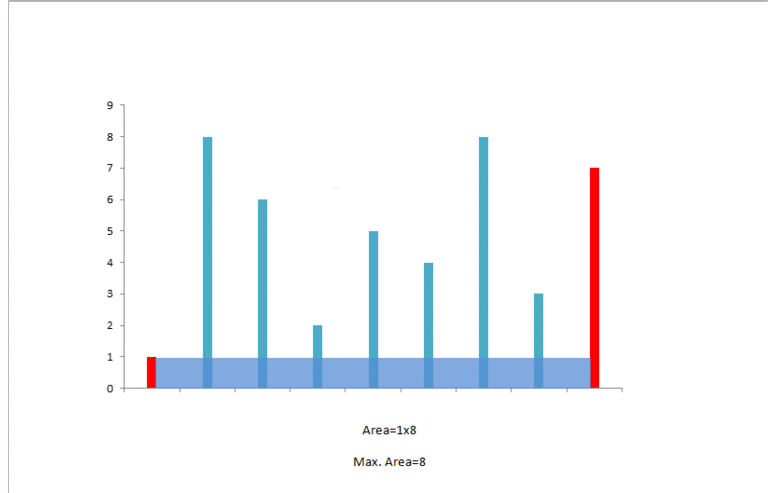
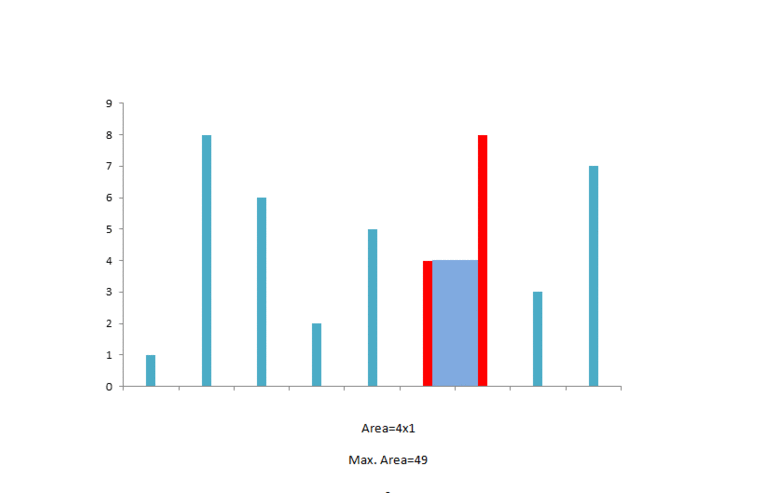
在初始时,左右指针分别指向数组的左右两端,它们可以容纳的水量为 。
此时我们需要移动一个指针。移动哪一个呢?直觉告诉我们,应该移动对应数字较小的那个指针(即此时的左指针)。这是因为,由于容纳的水量是由
决定的。如果我们移动数字较大的那个指针,那么前者「两个指针指向的数字中较小值」不会增加,后者「指针之间的距离」会减小,那么这个乘积会减小。因此,我们移动数字较大的那个指针是不合理的。因此,我们移动 数字较小的那个指针。
有读者可能会产生疑问:我们可不可以同时移动两个指针? 先别急,我们先假设 总是移动数字较小的那个指针 的思路是正确的,在走完流程之后,我们再去进行证明。
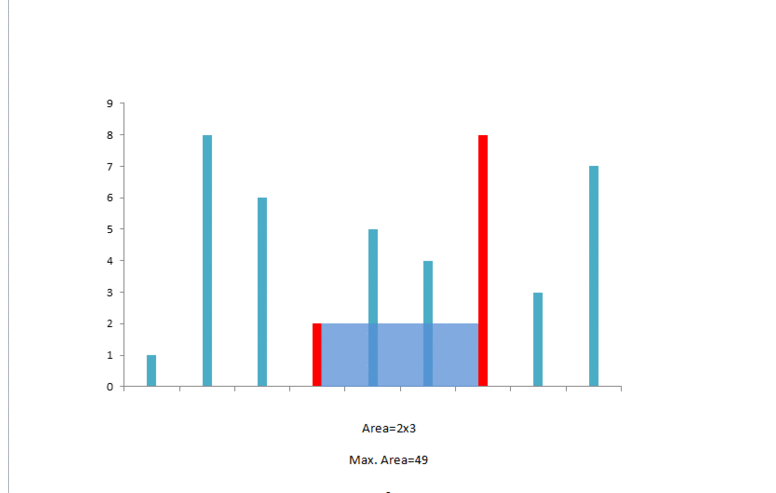
所以,我们将左指针向右移动:
[1, 8, 6, 2, 5, 4, 8, 3, 7]
^ ^
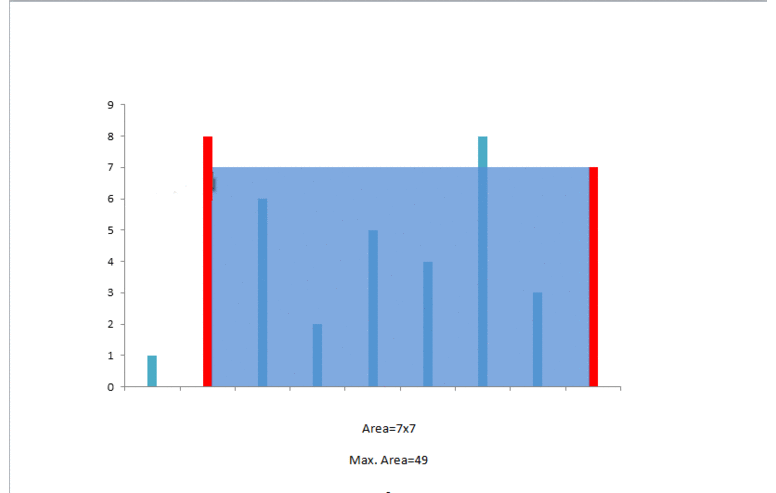
此时可以容纳的水量为 。由于右指针对应的数字较小,我们移动右指针:
[1, 8, 6, 2, 5, 4, 8, 3, 7]
^ ^
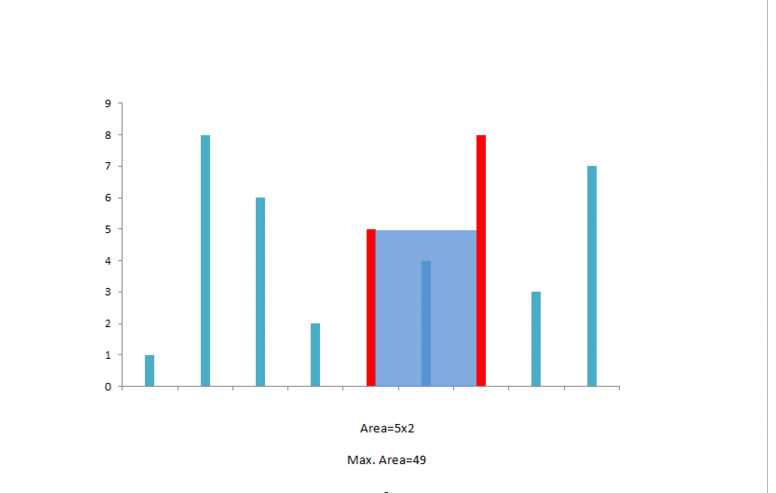
此时可以容纳的水量为 。由于右指针对应的数字较小,我们移动右指针:
[1, 8, 6, 2, 5, 4, 8, 3, 7]
^ ^
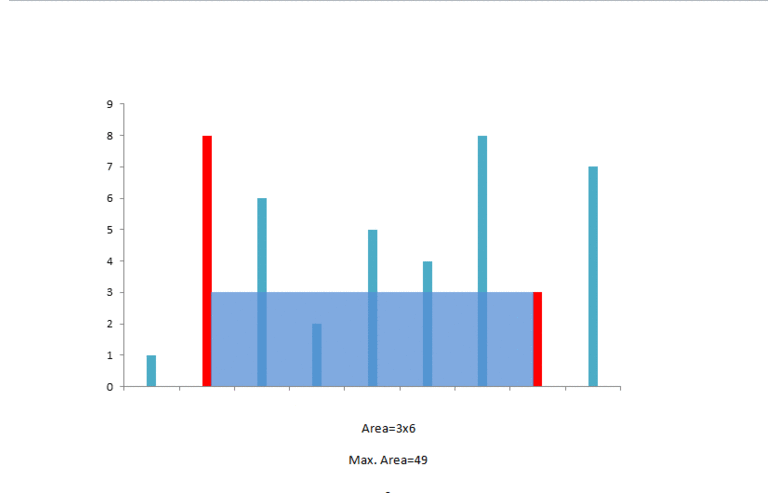
此时可以容纳的水量为 。两指针对应的数字相同,我们可以任意移动一个,例如左指针:
[1, 8, 6, 2, 5, 4, 8, 3, 7]
^ ^
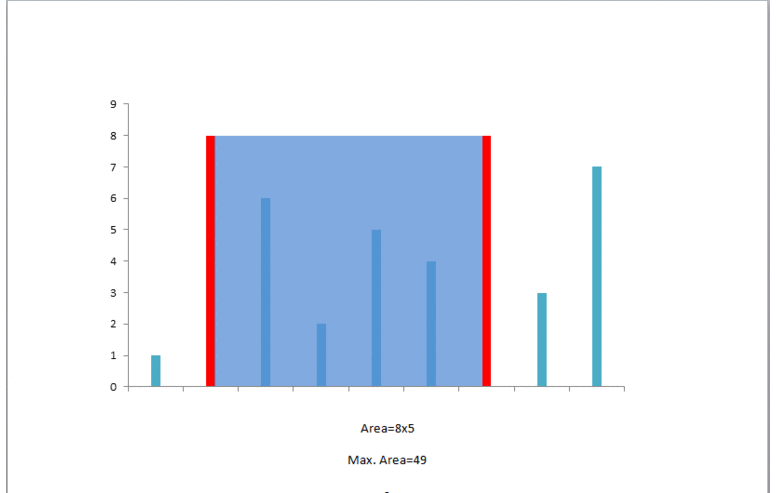
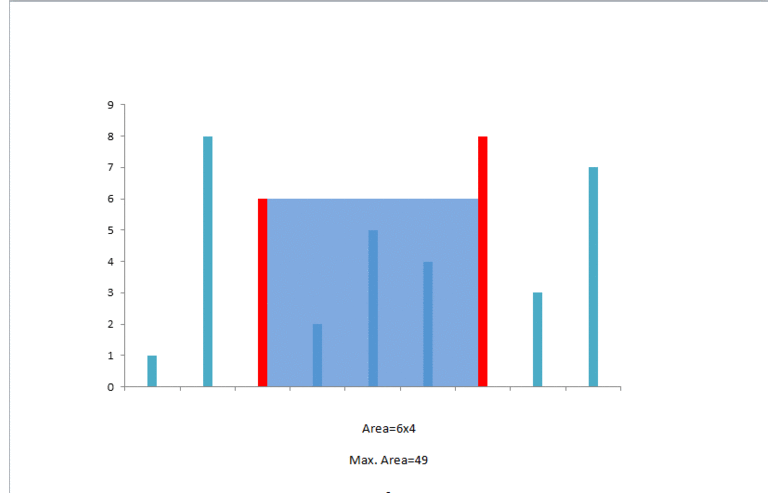
此时可以容纳的水量为 。由于左指针对应的数字较小,我们移动左指针,并且可以发现,在这之后左指针对应的数字总是较小,因此我们会一直移动左指针,直到两个指针重合。在这期间,对应的可以容纳的水量为:,,。
在我们移动指针的过程中,计算到的最多可以容纳的数量为 ,即为最终的答案。
下面的动画也给出了这个示例的过程:
证明
为什么双指针的做法是正确的?
双指针代表了什么?
双指针代表的是 可以作为容器边界的所有位置的范围。在一开始,双指针指向数组的左右边界,表示 数组中所有的位置都可以作为容器的边界,因为我们还没有进行过任何尝试。在这之后,我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置,就表示我们认为 这个指针不可能再作为容器的边界了。
为什么对应的数字较小的那个指针不可能再作为容器的边界了?
在上面的分析部分,我们对这个问题有了一点初步的想法。这里我们定量地进行证明。
考虑第一步,假设当前左指针和右指针指向的数分别为 和 ,不失一般性,我们假设 。同时,两个指针之间的距离为 。那么,它们组成的容器的容量为:
我们可以断定,如果我们保持左指针的位置不变,那么无论右指针在哪里,这个容器的容量都不会超过 了。注意这里右指针只能向左移动,因为 我们考虑的是第一步,也就是 指针还指向数组的左右边界的时候。
我们任意向左移动右指针,指向的数为 ,两个指针之间的距离为 ,那么显然有 ,并且 :
-
如果 ,那么 ;
-
如果 ,那么 。
因此有:
即无论我们怎么移动右指针,得到的容器的容量都小于移动前容器的容量。也就是说,这个左指针对应的数不会作为容器的边界了,那么我们就可以丢弃这个位置,将左指针向右移动一个位置,此时新的左指针于原先的右指针之间的左右位置,才可能会作为容器的边界。
这样以来,我们将问题的规模减小了 ,被我们丢弃的那个位置就相当于消失了。此时的左右指针,就指向了一个新的、规模减少了的问题的数组的左右边界,因此,我们可以继续像之前 考虑第一步 那样考虑这个问题:
-
求出当前双指针对应的容器的容量;
-
对应数字较小的那个指针以后不可能作为容器的边界了,将其丢弃,并移动对应的指针。
最后的答案是什么?
答案就是我们每次以双指针为左右边界(也就是「数组」的左右边界)计算出的容量中的最大值。
class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1;
int ans = 0;
while (l < r) {
int area = min(height[l], height[r]) * (r - l);
ans = max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
};
public class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int area = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
}
class Solution:
def maxArea(self, height: List[int]) -> int:
l, r = 0, len(height) - 1
ans = 0
while l < r:
area = min(height[l], height[r]) * (r - l)
ans = max(ans, area)
if height[l] <= height[r]:
l += 1
else:
r -= 1
return ans
复杂度分析
-
时间复杂度:,双指针总计最多遍历整个数组一次。
-
空间复杂度:,只需要额外的常数级别的空间。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号