leetcode题解之最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

方法一：水平扫描法

思路

首先，我们将描述一种查找一组字符串的最长公共前缀 $LCP(S_1 \ldots S_n)$ 的简单方法。
我们将会用到这样的结论：

$LCP(S_1 \ldots S_n) = LCP(LCP(LCP(S_1, S_2),S_3),\ldots S_n)$

算法

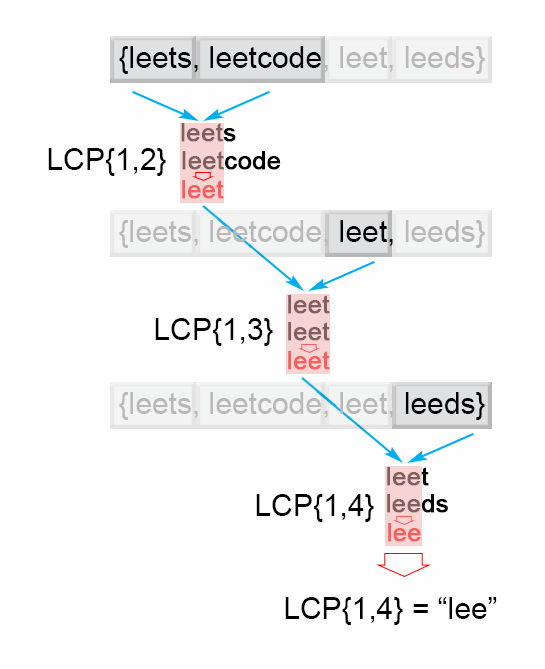
为了运用这种思想，算法要依次遍历字符串 $[S_1 \ldots S_n]$ ，当遍历到第 $i$ 个字符串的时候，找到最长公共前缀 $LCP(S_1 \ldots S_i)$ 。当 $LCP(S_1 \ldots S_i)$ 是一个空串的时候，算法就结束了。否则，在执行了 $n$ 次遍历之后，算法就会返回最终答案 $LCP(S_1 \ldots S_n)$ 。

图 1. 查找最长公共前缀（水平扫描法）

Java

public String longestCommonPrefix(String[] strs) {
   if (strs.length == 0) return "";
   String prefix = strs[0];
   for (int i = 1; i < strs.length; i++)
       while (strs[i].indexOf(prefix) != 0) {
           prefix = prefix.substring(0, prefix.length() - 1);
           if (prefix.isEmpty()) return "";
       }        
   return prefix;
}

复杂度分析

时间复杂度： $O(S)$ ，S 是所有字符串中字符数量的总和。

最坏的情况下， $n$ 个字符串都是相同的。算法会将 $S1$ 与其他字符串 $[S_2 \ldots S_n]$ 都做一次比较。这样就会进行 $S$ 次字符比较，其中 $S$ 是输入数据中所有字符数量。
空间复杂度： $O(1)$ ，我们只需要使用常数级别的额外空间。

算法二：水平扫描

算法

想象数组的末尾有一个非常短的字符串，使用上述方法依旧会进行 $S$ 次比较。优化这类情况的一种方法就是水平扫描。我们从前往后枚举字符串的每一列，先比较每个字符串相同列上的字符（即不同字符串相同下标的字符）然后再进行对下一列的比较。

Java

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";
    for (int i = 0; i < strs[0].length() ; i++){
        char c = strs[0].charAt(i);
        for (int j = 1; j < strs.length; j ++) {
            if (i == strs[j].length() || strs[j].charAt(i) != c)
                return strs[0].substring(0, i);             
        }
    }
    return strs[0];
}

复杂度分析

时间复杂度： $O(S)$ ，S 是所有字符串中字符数量的总和。

最坏情况下，输入数据为 $n$ 个长度为 $m$ 的相同字符串，算法会进行 $S = m*n$ 次比较。可以看到最坏情况下，本算法的效率与算法一相同，但是最好的情况下，算法只需要进行 $n*minLen$ 次比较，其中 $minLen$ 是数组中最短字符串的长度。
空间复杂度： $O(1)$ ，我们只需要使用常数级别的额外空间。

算法三：分治

思路

这个算法的思路来自于LCP操作的结合律。我们可以发现：
$LCP(S_1 \ldots S_n) = LCP(LCP(S_1 \ldots S_k), LCP (S_{k+1} \ldots S_n))$
，其中 $LCP(S_1 \ldots S_n)$ 是字符串 $[S_1 \ldots S_n]$ 的最长公共前缀， $1 < k < n$ 。

算法

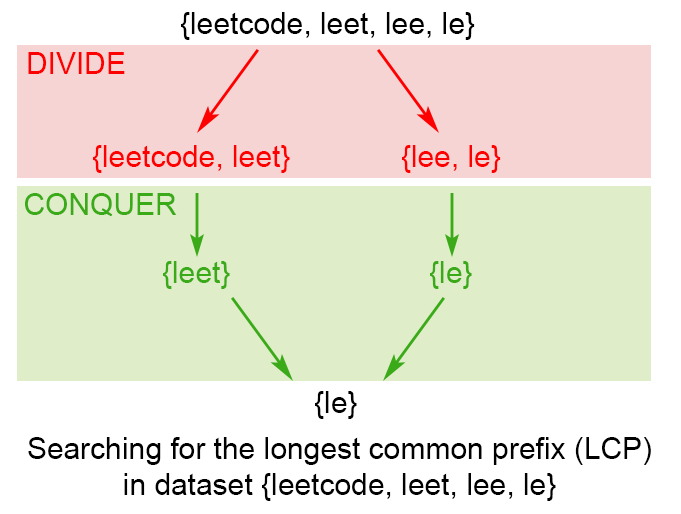
为了应用上述的结论，我们使用分治的技巧，将原问题 $LCP(S_i\cdots S_j)$ 分成两个子问题 $LCP(S_i\cdots S_{mid})$ 与 $LCP(S_{mid+1}, S_j)$ ，其中 mid = $\frac{i+j}{2}$ 。我们用子问题的解 lcpLeft 与 lcpRight 构造原问题的解 $LCP(S_i \cdots S_j)$ 。从头到尾挨个比较 lcpLeft 与 lcpRight 中的字符，直到不能再匹配为止。计算所得的 lcpLeft 与 lcpRight 最长公共前缀就是原问题的解 $LCP(S_i\cdots S_j)$ 。

图 2. 查找最长公共前缀的分治方法

Java

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";    
        return longestCommonPrefix(strs, 0 , strs.length - 1);
}
private String longestCommonPrefix(String[] strs, int l, int r) {

if (l == r) {

return strs[l];

}

else {

int mid = (l + r)/2;

String lcpLeft =   longestCommonPrefix(strs, l , mid);

String lcpRight =  longestCommonPrefix(strs, mid + 1,r);

return commonPrefix(lcpLeft, lcpRight);

}

}
String commonPrefix(String left,String right) {

int min = Math.min(left.length(), right.length());

for (int i = 0; i < min; i++) {

if ( left.charAt(i) != right.charAt(i) )

return left.substring(0, i);

}

return left.substring(0, min);

}

复杂度分析

最坏情况下，我们有 $n$ 个长度为 $m$ 的相同字符串。

时间复杂度： $O(S)$ ， $S$ 是所有字符串中字符数量的总和， $S=m*n$ 。

时间复杂度的递推式为 $T(n)=2\cdot T(\frac{n}{2})+O(m)$ ，化简后可知其就是 $O(S)$ 。最好情况下，算法会进行 $minLen\cdot n$ 次比较，其中 $minLen$ 是数组中最短字符串的长度。
空间复杂度： $O(m \cdot log(n))$

内存开支主要是递归过程中使用的栈空间所消耗的。一共会进行 $log(n)$ 次递归，每次需要 $m$ 的空间存储返回结果，所以空间复杂度为 $O(m\cdot log(n))$ 。

方法四：二分查找法

这个想法是应用二分查找法找到所有字符串的公共前缀的最大长度 L。算法的查找区间是 $(0 \ldots minLen)$ ，其中 minLen 是输入数据中最短的字符串的长度，同时也是答案的最长可能长度。每一次将查找区间一分为二，然后丢弃一定不包含最终答案的那一个。算法进行的过程中一共会出现两种可能情况：

S[1...mid] 不是所有串的公共前缀。这表明对于所有的 j > i S[1..j] 也不是公共前缀，于是我们就可以丢弃后半个查找区间。
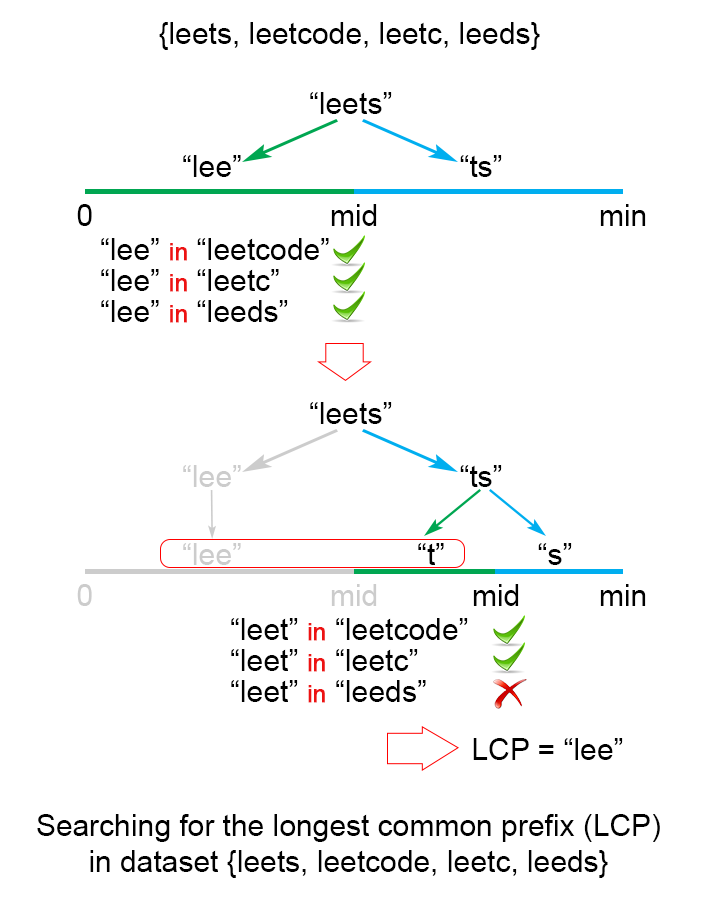
S[1...mid] 是所有串的公共前缀。这表示对于所有的 i < j S[1..i] 都是可行的公共前缀，因为我们要找最长的公共前缀，所以我们可以把前半个查找区间丢弃。

图 3. 使用二分查找法寻找最长公共前缀

Java

public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0)
        return "";
    int minLen = Integer.MAX_VALUE;
    for (String str : strs)
        minLen = Math.min(minLen, str.length());
    int low = 1;
    int high = minLen;
    while (low <= high) {
        int middle = (low + high) / 2;
        if (isCommonPrefix(strs, middle))
            low = middle + 1;
        else
            high = middle - 1;
    }
    return strs[0].substring(0, (low + high) / 2);
}
private boolean isCommonPrefix(String[] strs, int len){

String str1 = strs[0].substring(0,len);

for (int i = 1; i < strs.length; i++)

if (!strs[i].startsWith(str1))

return false;

return true;

}

复杂度分析

最坏情况下，我们有 $n$ 个长度为 $m$ 的相同字符串。

时间复杂度： $O(S \cdot log(n))$ ，其中 $S$ 所有字符串中字符数量的总和。

算法一共会进行 $log(n)$ 次迭代，每次一都会进行 $S = m*n$ 次比较，所以总时间复杂度为 $O(S \cdot log(n))$ 。
空间复杂度： $O(1)$ ，我们只需要使用常数级别的额外空间。

更进一步

让我们看一个有些不同的问题：

给定一些键值字符串 S = $[S_1,S_2 \ldots S_n]$ ，我们要找到字符串 q 与 S 的最长公共前缀。这样的查询操作可能会非常频繁。

我们可以通过将所有的键值 S 存储到一颗字典树中来优化最长公共前缀查询操作。如果你想学习更多关于字典树的内容，可以从 208. 实现 Trie (前缀树) 开始。在字典树中，从根向下的每一个节点都代表一些键值的公共前缀。但是我们需要找到字符串q 和所有键值字符串的最长公共前缀。这意味着我们需要从根找到一条最深的路径，满足以下条件：

这是所查询的字符串 q 的一个前缀
路径上的每一个节点都有且仅有一个孩子。否则，找到的路径就不是所有字符串的公共前缀
路径不包含被标记成某一个键值字符串结尾的节点。因为最长公共前缀不可能比某个字符串本身长

算法

最后的问题就是如何找到字典树中满足上述所有要求的最深节点。最有效的方法就是建立一颗包含字符串 $[S_1 \ldots S_n]$ 的字典树。然后在这颗树中匹配 q 的前缀。我们从根节点遍历这颗字典树，直到因为不能满足某个条件而不能再遍历为止。

图 4. 使用字典树查找最长公共前缀

Java

public String longestCommonPrefix(String q, String[] strs) {
    if (strs == null || strs.length == 0)
         return "";  
    if (strs.length == 1)
         return strs[0];
    Trie trie = new Trie();      
    for (int i = 1; i < strs.length ; i++) {
        trie.insert(strs[i]);
    }
    return trie.searchLongestPrefix(q);
}
class TrieNode {
<span class="hljs-comment">// 子节点的链接数组</span>
<span class="hljs-keyword">private</span> TrieNode[] links;

<span class="hljs-keyword">private</span> <span class="hljs-keyword">final</span> <span class="hljs-keyword">int</span> R = <span class="hljs-number">26</span>;

<span class="hljs-keyword">private</span> <span class="hljs-keyword">boolean</span> isEnd;

<span class="hljs-comment">// 非空子节点的数量</span>
<span class="hljs-keyword">private</span> <span class="hljs-keyword">int</span> size;    
<span class="hljs-function"><span class="hljs-keyword">public</span> <span class="hljs-keyword">void</span> <span class="hljs-title">put</span><span class="hljs-params">(<span class="hljs-keyword">char</span> ch, TrieNode node)</span> </span>{
    links[ch -<span class="hljs-string">'a'</span>] = node;
    size++;
}

<span class="hljs-function"><span class="hljs-keyword">public</span> <span class="hljs-keyword">int</span> <span class="hljs-title">getLinks</span><span class="hljs-params">()</span> </span>{
    <span class="hljs-keyword">return</span> size;
}
<span class="hljs-comment">// 假设方法 containsKey、isEnd、get、put 都已经实现了</span>
<span class="hljs-comment">// 可以参考文章：https://leetcode.com/articles/implement-trie-prefix-tree/</span>

}
public class Trie {
<span class="hljs-keyword">private</span> TrieNode root;

<span class="hljs-function"><span class="hljs-keyword">public</span> <span class="hljs-title">Trie</span><span class="hljs-params">()</span> </span>{
    root = <span class="hljs-keyword">new</span> TrieNode();
}

// 假设方法 insert、search、searchPrefix 都已经实现了

// 可以参考文章：https://leetcode.com/articles/implement-trie-prefix-tree/

private String searchLongestPrefix(String word) {

TrieNode node = root;

StringBuilder prefix = new StringBuilder();

for (int i = 0; i < word.length(); i++) {

char curLetter = word.charAt(i);

if (node.containsKey(curLetter) && (node.getLinks() == 1) && (!node.isEnd())) {

prefix.append(curLetter);

node = node.get(curLetter);

}

else

return prefix.toString();
     }
     <span class="hljs-keyword">return</span> prefix.toString();
}

}

复杂度分析

最坏情况下查询字符串 $q$ 的长度为 $m$ 并且它与数组中 $n$ 个字符串均相同。

时间复杂度：预处理过程 $O(S)$ ，其中 $S$ 数组里所有字符串中字符数量的总和，最长公共前缀查询操作的复杂度为 $O(m)$ 。

建立字典树的时间复杂度为 $O(S)$ 。在字典树中查找字符串 $q$ 的最长公共前缀在最坏情况下需要 $O(m)$ 的时间。
空间复杂度： $O(S)$ ，我们只需要使用额外的 $S$ 空间建立字典树。

posted @ 2020-06-08 11:13 刷题之路1 阅读(311) 评论(0) 收藏举报

刷新页面返回顶部