最小生成树(MST)

转自：https://www.cnblogs.com/fanmu/p/6082152.html

最小生成树

1.定义

2.kruskal 算法

3.Prim 算法

1.定义

G=(V,E)为连通无向图，V为结点的集合，E为结点的可能连接边

对每条边(u ,v)都赋予权重w(u ,v)

目标：找到一个无环子集T, 既能将所有结点连接起来，又具有最小权重。

T是由G生成的树，并把这种问题叫做最小生成树问题。

2.kruskal算法

主要思想：

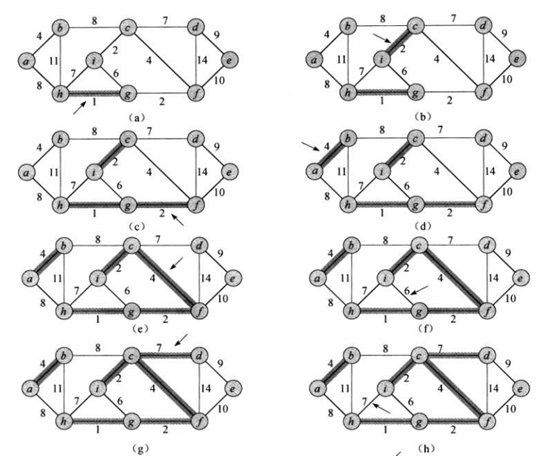
将V的每个结点定义为一棵树，并定义根节点（代表）为该节点，将E中的边按权重从小到大依次处理。

首先判断边的两个结点是否属于同一棵树（根据根节点是否一致），若不是，则合并两棵树，并更新根节点；若是，则不予理会。

（这里是为了形成无环集合，保证权重和最小

如下图f所示，结点i、g已合并为一棵树，根节点一致，所以ig边不再纳入集合）

global G
G.VV=char(97:105);
G.V=cell(9,1);
G.Adj={'ab';'ah';'bc';'bh';'hi';'hg';'ig';'gf';'cf';'cd';'df';'de';'ef';'ic'};
G.Bdj=[4;8;8;11;7;1;6;2;4;7;14;9;10;2];
A=[];
for i=1:length(G.VV) %MAKE-SET
    G.V{i}.p=G.VV(i);
    G.V{i}.rank=0;
end
[wei,index]=sort(G.Bdj);
la=G.Adj(index);
for i=1:length(la)
    x=la{i};
    a1=find(G.VV==x(1));
    a2=find(G.VV==x(2));
    if find_set(a1)~=find_set(a2)
        A=[A;x];
        union(a1,a2);
    end
end
 
 
function  k= find_set(i)
%找到集合的代表，也就是根节点
global G
if G.V{i}.p~=G.VV(i)%这里的G.V{i}.p是G.VV(i)所在子树的根节点
    %函数的目标是找到合并之后的树（集合）的的结点
    j=find(G.VV==G.V{i}.p);
    G.V{i}.p=find_set(j);%不断更新，直到找到集合的根节点
end
k=G.V{i}.p;
end
 
function union(i,a)
%合并两个集合，并更新集合的根节点
%更新的原则是看子树的结点数目，多的那个的子树的代表当根节点
%注意，这里并没有更新子树的根节点，这一步骤是在find_set里完成的
global G
x=find_set(i);
y=find_set(a);
aa=find(G.VV==x);
bb=find(G.VV==y);
if G.V{aa}.rank>G.V{bb}.rank
    G.V{bb}.p=G.VV(aa);
else
    G.V{aa}.p=G.VV(bb);
    if G.V{aa}.rank==G.V{bb}.rank
        G.V{bb}.rank=G.V{bb}.rank+1;
    end
end 
end

运行结果：

A =

hg
gf
ic
ab
cf
cd
ah
de

d=37

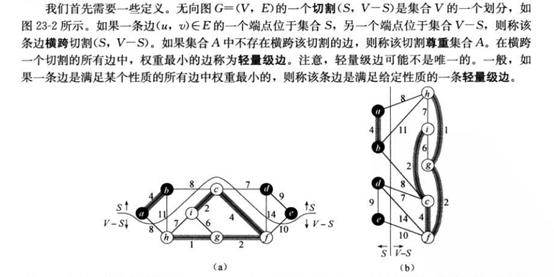
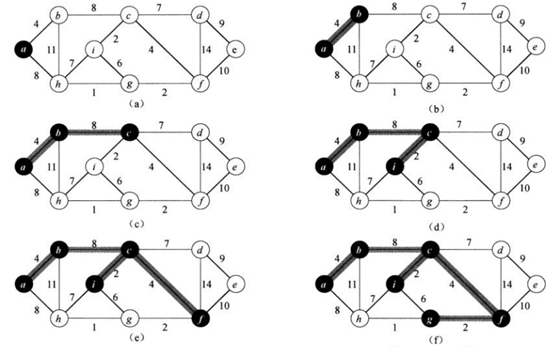
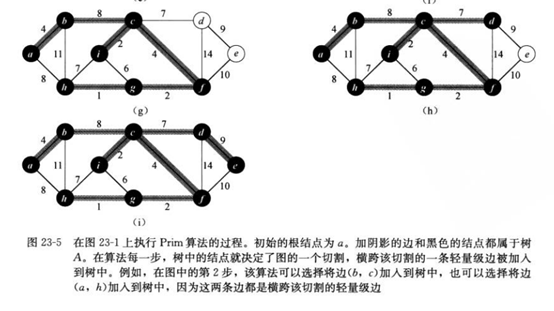
3.prim 算法

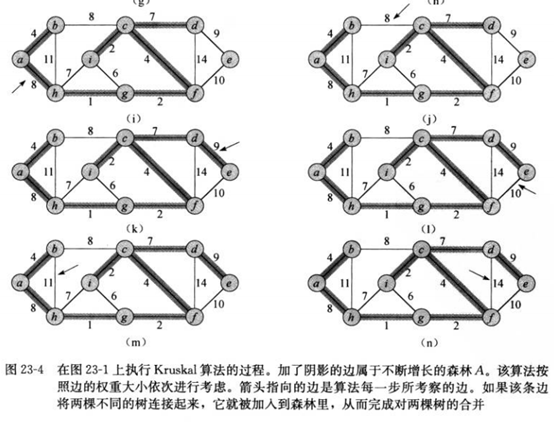
关于轻量级边的定义：

主要思想：

给定连通图G和任意根节点r，最小生成树从结点r开始，一直长大到覆盖V中所有结点为止，即不断寻找轻量级边以实现最小权重和

%最小生成树-prim算法
G.VV=char(97:105);
G.Adj={'bh';'ahc';'bifd';'cfe';'df';'cdeg';'ihf';'abig';'cgh'};%邻接链表
G.Bdj={[4 8];[4 11 8];[8 2 4 7];[7 14 9];[9 10];[4 14 10 2];[6 1 2];[8 11 7 1];[2 6 7]};%邻接链表对应权重
Q=G.VV;
Q(Q==G.VV(1))=[];
r=1;
x(r)=G.VV(1);%给定初始点
d=0;
 
while length(Q)~=0
    [wei,index]=sort(unionwei(G,x,r));%！！！关键点，目的是横跨（V-Q,Q）的轻量级边的一个端点，即权重最小的一个点
    u=unionla(G,x,r);
    u=u(index);
    for i=1:length(u)
        if find(Q==u(i))
            k=i;
            break;
        end
    end
    d=d+wei(k);
    r=r+1;
    x(r)=u(k);
         
    Q(Q==u(k))=[];%找到后Q中删除，以保证每个点只被访问一次
end
fprintf('path:');x
fprint('\n');
fprintf('d= %d \n',d);
 
 
function wei0=unionwei( G,x,r )
%合并权重向量，方便排序
wei0=[];
for i=1:r
    a=find(G.VV==x(i));
    wei1=G.Bdj{a};
    wei0=[wei0 wei1];
end
end
 
function la0 = unionla(G,x, r )
%合并权重对应的边
la0=[];
for i=1:r
    a=find(G.VV==x(i));
    la1=G.Adj{a};
    la0=[la0 la1];
end
end

运行结果：

path:
x =

abhgfcide

d= 37

posted @ 2018-12-26 15:49 Le1B_o 阅读(301) 评论(0) 收藏举报

刷新页面返回顶部

LeeB_o

最小生成树(MST)

公告