个人博客：https://luxialan.com

机器学习基础（三）Logistic回归模型 分类： 机器学习 2015-01-18 10:50 85人阅读 评论(0) 收藏

Logistic回归模型是引入Logistic函数后对线性回归模型进行的归一化处理:


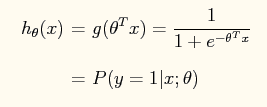
这样处理的结果是输出的结果在[0,1]之内，避免了某个特征影响过大。从概率的角度，我们可以将其理解为某个事件发生的可能性。

代价函数为：

\begin{displaymath}J(\theta)=\frac{{1}}{m}\sum_{i=1}^{m}\left[-y^{(i)}\log(h_......(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))\right] \nonumber\par\end{displaymath}

这个代价函数的推导涉及到极大似然估计，推导如下：


整合上面两式：


在独立同分布的前提下，似然函数：


取对数：


可以看出代价函数多了一步均值化处理。

对于Logistic回归模型的求解有两种方法：梯度下降法和牛顿法

梯度下降法求解


得到

这里我们可以看出Logistic函数本身也具有许多良好的性质，比如其导数：



牛顿法：http://en.wikipedia.org/wiki/Newton%27s_method

File:NewtonIteration Ani.gif

牛顿法的迭代模型：


扩展到高维：

\begin{displaymath}\theta^{(t+1)}=\theta^{(t)}-H^{-1}\nabla_{\theta}J \nonumber\end{displaymath}

其中

\begin{displaymath}\nabla_{\theta}J = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)} \nonumber \nonumber\end{displaymath}

\begin{displaymath}H & = & \frac{1}{m}\sum_{i=1}^{m}\left[h_{\theta}(x^{(i)})\l......^{(i)})\right)x^{(i)}\left(x^{(i)}\right)^{T}\right] \nonumber\end{displaymath}


参考资料：

http://www.netfoucs.com/article/yangliuy/62606.html

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=MachineLearning&doc=exercises/ex4/ex4.html

http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=MachineLearning

http://hi.baidu.com/hehehehello/item/40025c33d7d9b7b9633aff87#send


版权声明：本文为博主原创文章，未经博主允许不得转载。

posted @ 2015-01-18 10:50  luxialan  阅读(162)  评论(0)    收藏  举报