21-2 使用友元重载算术运算符
C++中最常用的运算符是算术运算符——即加号运算符(+)、减号运算符(-)、乘号运算符(*)和除号运算符(/)注意所有算术运算符都是二元运算符,即它们需要两个操作数——运算符两侧各一个。这四个运算符都采用完全相同的方式重载。
运算符重载主要有三种实现方式:成员函数方式、友元函数方式和普通函数方式。本节课将重点讲解友元函数方式(因其对大多数二元运算符而言更直观)。下节课将探讨普通函数方式。本章后续课程中,我们将最终讲解成员函数方式。当然,我们还会详细总结每种方式的适用场景。
使用友元函数重载运算符
考虑以下类:
class Cents
{
private:
int m_cents {};
public:
Cents(int cents) : m_cents{ cents } { }
int getCents() const { return m_cents; }
};
以下示例展示了如何重载加法运算符 (+),以便将两个“Cents”对象相加:
#include <iostream>
class Cents
{
private:
int m_cents {};
public:
Cents(int cents) : m_cents{ cents } { }
// add Cents + Cents using a friend function
friend Cents operator+(const Cents& c1, const Cents& c2);
int getCents() const { return m_cents; }
};
// note: this function is not a member function!
Cents operator+(const Cents& c1, const Cents& c2)
{
// use the Cents constructor and operator+(int, int)
// we can access m_cents directly because this is a friend function
return c1.m_cents + c2.m_cents;
}
int main()
{
Cents cents1{ 6 };
Cents cents2{ 8 };
Cents centsSum{ cents1 + cents2 };
std::cout << "I have " << centsSum.getCents() << " cents.\n";
return 0;
}
这产生了以下结果:
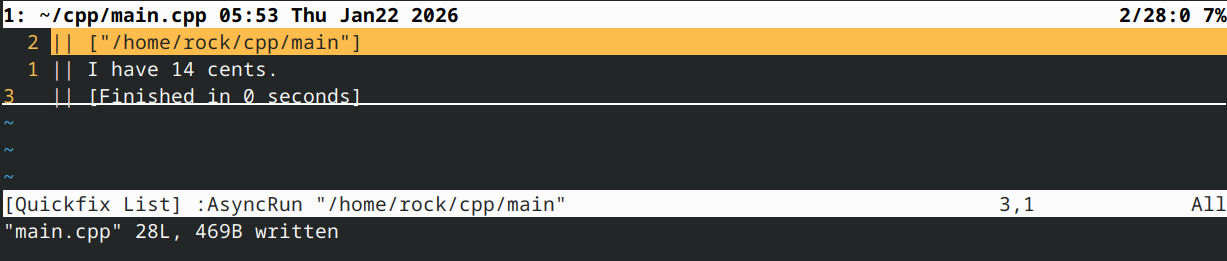
重载加号运算符(+)的过程非常简单:声明一个名为operator+的函数,为其指定两个与待加运算数类型相同的参数,选择合适的返回类型,然后编写函数体即可。
对于我们的Cents对象而言,实现operator+()函数非常简单。首先确定参数类型:本版本的加法运算符用于合并两个Cents对象,因此函数需接收两个Cents类型的对象。其次确定返回类型:加法运算结果应为Cents类型,故将其设为返回类型。
最后实现逻辑:要合并两个Cents对象,需将各自的m_cents成员相加。由于重载的 operator+() 函数是该类的友元函数,我们可以直接访问参数的 m_cents 成员。此外,由于 m_cents 是整型变量,而 C++ 通过内置的加法运算符(适用于整数操作数)已具备整数加法功能,因此我们只需使用 + 运算符即可完成加法运算。
重载减法运算符 (-) 同样简单:
#include <iostream>
class Cents
{
private:
int m_cents {};
public:
explicit Cents(int cents) : m_cents{ cents } { }
// add Cents + Cents using a friend function
friend Cents operator+(const Cents& c1, const Cents& c2);
// subtract Cents - Cents using a friend function
friend Cents operator-(const Cents& c1, const Cents& c2);
int getCents() const { return m_cents; }
};
// note: this function is not a member function!
Cents operator+(const Cents& c1, const Cents& c2)
{
// use the Cents constructor and operator+(int, int)
// we can access m_cents directly because this is a friend function
return Cents { c1.m_cents + c2.m_cents };
}
// note: this function is not a member function!
Cents operator-(const Cents& c1, const Cents& c2)
{
// use the Cents constructor and operator-(int, int)
// we can access m_cents directly because this is a friend function
return Cents { c1.m_cents - c2.m_cents };
}
int main()
{
Cents cents1{ 6 };
Cents cents2{ 2 };
Cents centsSum{ cents1 - cents2 };
std::cout << "I have " << centsSum.getCents() << " cents.\n";
return 0;
}
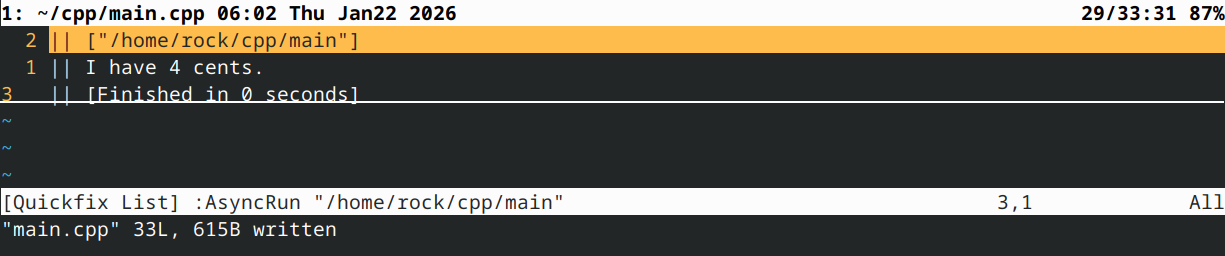
重载乘法运算符()和除法运算符(/)就像分别定义operator和operator/函数一样简单。
友元函数可以在类内部定义
尽管友元函数并非类的成员,但若需要,仍可将其定义在类内部:
#include <iostream>
class Cents
{
private:
int m_cents {};
public:
explicit Cents(int cents) : m_cents{ cents } { }
// add Cents + Cents using a friend function
// This function is not considered a member of the class, even though the definition is inside the class
friend Cents operator+(const Cents& c1, const Cents& c2)
{
// use the Cents constructor and operator+(int, int)
// we can access m_cents directly because this is a friend function
return Cents { c1.m_cents + c2.m_cents };
}
int getCents() const { return m_cents; }
};
int main()
{
Cents cents1{ 6 };
Cents cents2{ 8 };
Cents centsSum{ cents1 + cents2 };
std::cout << "I have " << centsSum.getCents() << " cents.\n";
return 0;
}
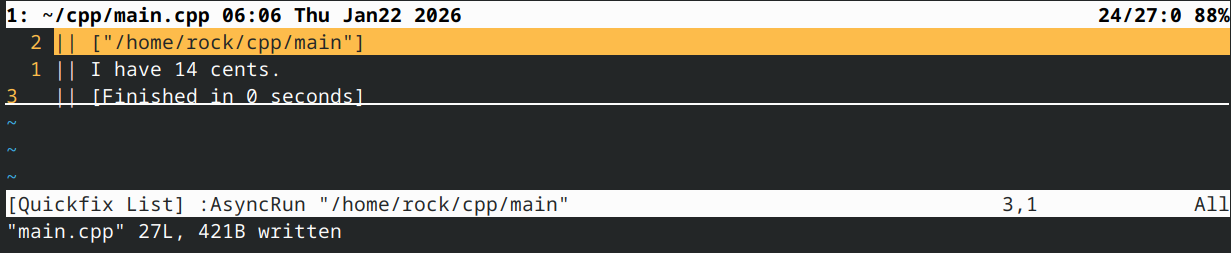
对于实现简单的重载运算符而言,这完全没问题。
为不同类型的操作数重载运算符
通常情况下,您希望重载的运算符能够处理不同类型的操作数。例如,对于 Cents(4) 表达式,我们可能需要向其添加整数 6 以得到结果 Cents(10)。
当C++评估表达式x + y时,x成为第一个参数,y成为第二个参数。当x和y类型相同时,无论采用x + y还是y + x的顺序,调用的都是同一个版本的operator+。但当操作数类型不同时,x + y与y + x调用的函数并不相同。
例如,Cents(4) + 6 将调用 operator+(Cents, int),而 6 + Cents(4) 将调用 operator+(int, Cents)。因此,当为不同类型的操作数重载二元运算符时,我们实际上需要编写两个函数——分别处理两种情况。以下是一个示例:
#include <iostream>
class Cents
{
private:
int m_cents {};
public:
explicit Cents(int cents) : m_cents{ cents } { }
// add Cents + int using a friend function
friend Cents operator+(const Cents& c1, int value);
// add int + Cents using a friend function
friend Cents operator+(int value, const Cents& c1);
int getCents() const { return m_cents; }
};
// note: this function is not a member function!
Cents operator+(const Cents& c1, int value)
{
// use the Cents constructor and operator+(int, int)
// we can access m_cents directly because this is a friend function
return Cents { c1.m_cents + value };
}
// note: this function is not a member function!
Cents operator+(int value, const Cents& c1)
{
// use the Cents constructor and operator+(int, int)
// we can access m_cents directly because this is a friend function
return Cents { c1.m_cents + value };
}
int main()
{
Cents c1{ Cents{ 4 } + 6 };
Cents c2{ 6 + Cents{ 4 } };
std::cout << "I have " << c1.getCents() << " cents.\n";
std::cout << "I have " << c2.getCents() << " cents.\n";
return 0;
}
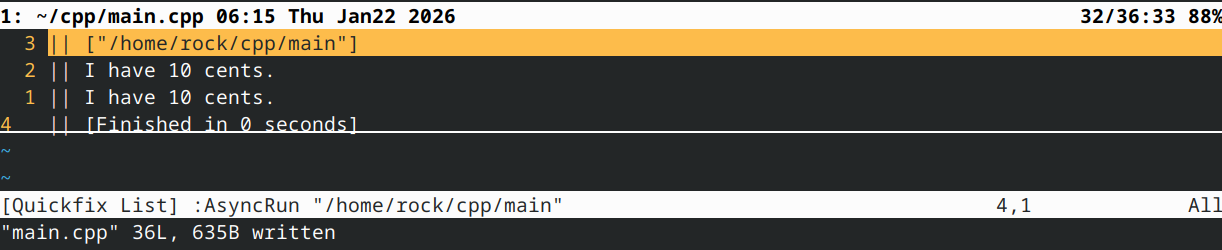
请注意,这两个重载函数具有相同的实现——这是因为它们执行相同的功能,只是参数的接收顺序不同。
另一个例子
让我们再看一个例子:
#include <iostream>
class MinMax
{
private:
int m_min {}; // The min value seen so far
int m_max {}; // The max value seen so far
public:
MinMax(int min, int max)
: m_min { min }, m_max { max }
{ }
int getMin() const { return m_min; }
int getMax() const { return m_max; }
friend MinMax operator+(const MinMax& m1, const MinMax& m2);
friend MinMax operator+(const MinMax& m, int value);
friend MinMax operator+(int value, const MinMax& m);
};
MinMax operator+(const MinMax& m1, const MinMax& m2)
{
// Get the minimum value seen in m1 and m2
int min{ m1.m_min < m2.m_min ? m1.m_min : m2.m_min };
// Get the maximum value seen in m1 and m2
int max{ m1.m_max > m2.m_max ? m1.m_max : m2.m_max };
return MinMax { min, max };
}
MinMax operator+(const MinMax& m, int value)
{
// Get the minimum value seen in m and value
int min{ m.m_min < value ? m.m_min : value };
// Get the maximum value seen in m and value
int max{ m.m_max > value ? m.m_max : value };
return MinMax { min, max };
}
MinMax operator+(int value, const MinMax& m)
{
// calls operator+(MinMax, int)
return m + value;
}
int main()
{
MinMax m1{ 10, 15 };
MinMax m2{ 8, 11 };
MinMax m3{ 3, 12 };
MinMax mFinal{ m1 + m2 + 5 + 8 + m3 + 16 };
std::cout << "Result: (" << mFinal.getMin() << ", " <<
mFinal.getMax() << ")\n";
return 0;
}
MinMax类用于记录其迄今为止遇到的最小值和最大值。我们重载了+运算符三次,以便能够将两个MinMax对象相加,或将整数与MinMax对象相加。
此示例将产生以下结果:
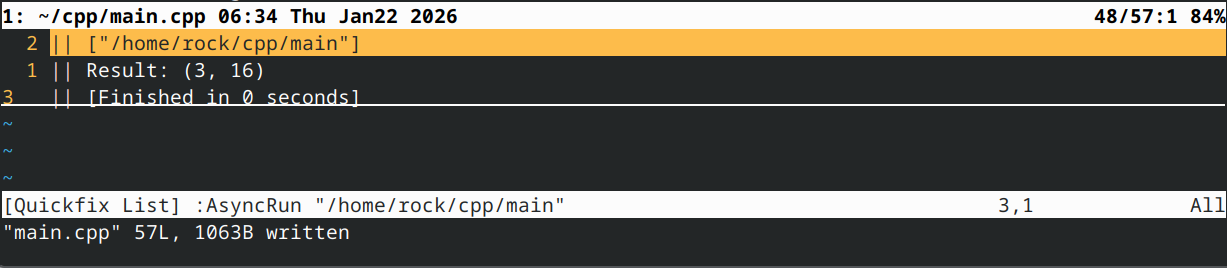
你会注意到这是我们添加到mFinal中的最小值和最大值。
让我们进一步探讨“MinMax mFinal { m1 + m2 + 5 + 8 + m3 + 16 }”的求值过程。请记住运算符+从左到右求值,因此m1 + m2将首先计算。这将转化为对运算符+(m1, m2)的调用,产生返回值MinMax(8, 15)。接着计算MinMax(8, 15) + 5,这将转化为对运算符+(MinMax(8, 15), 5)的调用,产生返回值MinMax(5, 15)。接着 MinMax(5, 15) + 8 以相同方式求值得到 MinMax(5, 15)。随后 MinMax(5, 15) + m3 求值得到 MinMax(3, 15)。最后 MinMax(3, 15) + 16 求值为 MinMax(3, 16)。该最终结果用于初始化 mFinal。
换言之,该表达式可视为“MinMax mFinal = (((((m1 + m2) + 5) + 8) + m3) + 16)”,每次运算返回的 MinMax 对象将作为后续运算符的左操作数。
使用其他运算符实现运算符
在上例中,请注意我们通过调用 operator+(MinMax, int) 来定义 operator+(int, MinMax)(两者结果相同)。这使我们能够将 operator+(int, MinMax) 的实现压缩为一行代码,通过减少冗余使代码更易维护,并简化函数的理解难度。
通过调用其他重载运算符来定义重载运算符的做法很常见。当这种方式能简化代码时,就应该采用。对于实现非常简单的情况(例如仅需一行代码),是否采用这种方式则需权衡利弊。
测验时间
问题 #1
a) 编写一个名为 Fraction 的类,该类包含一个整型分子和分母成员变量。编写一个 print() 函数,用于输出该分数。
以下代码应能编译通过:
#include <iostream>
int main()
{
Fraction f1{ 1, 4 };
f1.print();
Fraction f2{ 1, 2 };
f2.print();
return 0;
}
这应该输出:
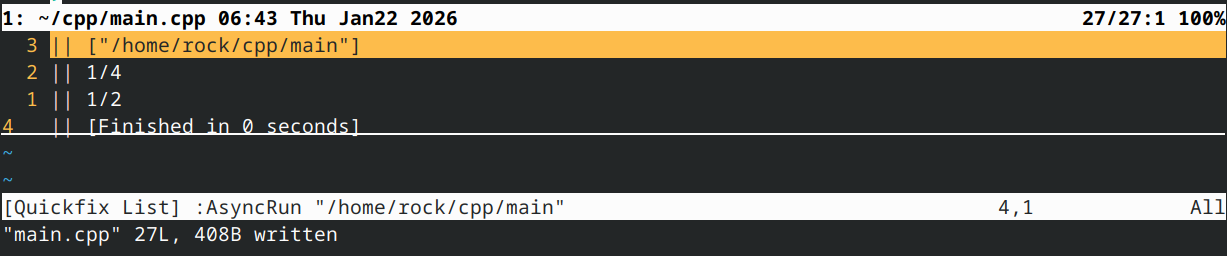
显示答案
#include <iostream>
class Fraction
{
private:
int m_numerator { 0 };
int m_denominator { 1 };
public:
explicit Fraction(int numerator, int denominator=1)
: m_numerator{numerator}, m_denominator{denominator}
{
}
void print() const
{
std::cout << m_numerator << '/' << m_denominator << '\n';
}
};
int main()
{
Fraction f1 {1, 4};
f1.print();
Fraction f2 {1, 2};
f2.print();
return 0;
}
b) 添加重载的乘法运算符,用于处理分数与整数的乘法运算以及两个分数之间的乘法运算。采用友元函数方法实现。
提示:两个分数相乘时,先将两个分子相乘,再将两个分母相乘。分数与整数相乘时,将分数的分子与整数相乘,分母保持不变。
以下代码应能编译通过:
#include <iostream>
int main()
{
Fraction f1{2, 5};
f1.print();
Fraction f2{3, 8};
f2.print();
Fraction f3{ f1 * f2 };
f3.print();
Fraction f4{ f1 * 2 };
f4.print();
Fraction f5{ 2 * f2 };
f5.print();
Fraction f6{ Fraction{1, 2} * Fraction{2, 3} * Fraction{3, 4} };
f6.print();
return 0;
}
这将输出
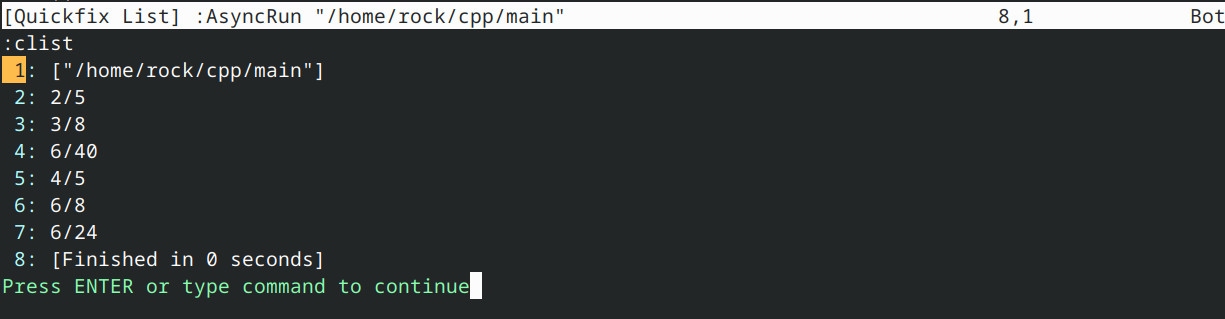
显示解决方案
#include <iostream>
class Fraction
{
private:
int m_numerator { 0 };
int m_denominator { 1 };
public:
explicit Fraction(int numerator, int denominator=1)
: m_numerator{numerator}, m_denominator{denominator}
{
}
// We don't want to pass by value, because copying is slow.
// We can't and shouldn't pass by non-const reference, because then
// our functions wouldn't work with r-values.
friend Fraction operator*(const Fraction& f1, const Fraction& f2);
friend Fraction operator*(const Fraction& f1, int value);
friend Fraction operator*(int value, const Fraction& f1);
void print() const
{
std::cout << m_numerator << '/' << m_denominator << '\n';
}
};
Fraction operator*(const Fraction& f1, const Fraction& f2)
{
return Fraction { f1.m_numerator * f2.m_numerator, f1.m_denominator * f2.m_denominator };
}
Fraction operator*(const Fraction& f1, int value)
{
return Fraction { f1.m_numerator * value, f1.m_denominator };
}
Fraction operator*(int value, const Fraction& f1)
{
return Fraction { f1 * value };
}
int main()
{
Fraction f1{2, 5};
f1.print();
Fraction f2{3, 8};
f2.print();
Fraction f3{ f1 * f2 };
f3.print();
Fraction f4{ f1 * 2 };
f4.print();
Fraction f5{ 2 * f2 };
f5.print();
Fraction f6{ Fraction{1, 2} * Fraction{2, 3} * Fraction{3, 4} };
f6.print();
return 0;
}
c) 如果我们将构造函数改为非显式构造函数,并移除先前解决方案中的整数乘法运算符,程序为何仍能正常运行?
// Remove explicit from constructor
Fraction(int numerator, int denominator=1)
: m_numerator{numerator}, m_denominator{denominator}
{
}
// We can remove these operators, and the program continues to work
Fraction operator*(const Fraction& f1, int value);
Fraction operator*(int value, const Fraction& f1);
显示答案
我们仍然有
`Fraction operator*(const Fraction& f1, const Fraction& f2)`
当我们用一个分数乘以一个整数时,例如
`Fraction f5{ 2 * f2 };`
未显式定义的 Fraction(int, int) 构造函数将用于从 2 构造一个新的 Fraction。随后使用 Fraction * Fraction 运算符将该新 Fraction 与 f2 相乘。
由于此过程需要将 2 转换为 Fraction,因此相较于使用整数乘法重载运算符的实现,此方法速度稍慢。
d) 若将运算符*(Fraction, Fraction)的引用参数设为非const,主函数中的以下代码行将失效。原因何在?
// The non-const multiplication operator looks like this
Fraction operator*(Fraction& f1, Fraction& f2)
// This doesn't work anymore
Fraction f6{ Fraction{1, 2} * Fraction{2, 3} * Fraction{3, 4} };
显示答案
我们正在对临时Fraction对象进行乘法运算,但非const引用无法绑定到临时对象。
e) 附加题:分数 2/4 与 1/2 相同,但 2/4 尚未化简为最简形式。我们可通过求分子与分母的最大公约数(GCD),再将分子和分母同时除以该最大公约数,将任意给定分数化简为最简形式。
C++17标准库(位于
若使用旧版编译器,可通过以下函数计算GCD:
#include <cmath> // for std::abs
int gcd(int a, int b) {
return (b == 0) ? std::abs(a) : gcd(b, a % b);
}
编写一个名为 reduce() 的成员函数,用于对分数进行约分。确保所有分数都能正确约分。
以下代码应能编译通过:
#include <iostream>
int main()
{
Fraction f1{2, 5};
f1.print();
Fraction f2{3, 8};
f2.print();
Fraction f3{ f1 * f2 };
f3.print();
Fraction f4{ f1 * 2 };
f4.print();
Fraction f5{ 2 * f2 };
f5.print();
Fraction f6{ Fraction{1, 2} * Fraction{2, 3} * Fraction{3, 4} };
f6.print();
Fraction f7{0, 6};
f7.print();
return 0;
}
并输出结果:
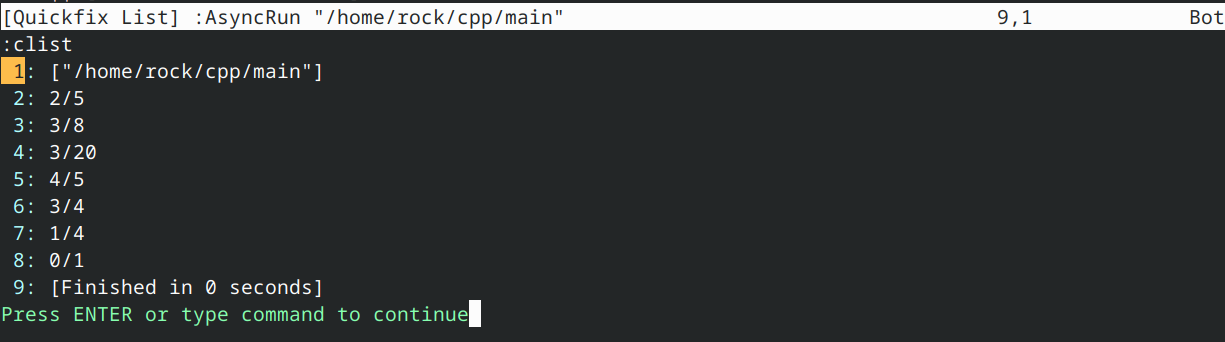
解决方案:
#include <iostream>
#include <numeric> // for std::gcd
// This version of the Fraction class auto-reduces fractions
class Fraction
{
private:
int m_numerator{ 0 };
int m_denominator{ 1 };
public:
explicit Fraction(int numerator, int denominator = 1)
: m_numerator{ numerator }, m_denominator{ denominator }
{
// We put reduce() in the constructor to ensure any fractions we make get reduced!
// Since all of the overloaded operators create new Fractions, we can guarantee this will get called here
reduce();
}
void reduce()
{
int gcd{ std::gcd(m_numerator, m_denominator) };
if (gcd) // Make sure we don't try to divide by 0
{
m_numerator /= gcd;
m_denominator /= gcd;
}
}
friend Fraction operator*(const Fraction& f1, const Fraction& f2);
friend Fraction operator*(const Fraction& f1, int value);
friend Fraction operator*(int value, const Fraction& f1);
void print() const
{
std::cout << m_numerator << '/' << m_denominator << '\n';
}
};
Fraction operator*(const Fraction& f1, const Fraction& f2)
{
return Fraction { f1.m_numerator * f2.m_numerator, f1.m_denominator * f2.m_denominator };
}
Fraction operator*(const Fraction& f1, int value)
{
return Fraction { f1.m_numerator * value, f1.m_denominator };
}
Fraction operator*(int value, const Fraction& f1)
{
return Fraction { f1 * value };
}
int main()
{
Fraction f1{ 2, 5 };
f1.print();
Fraction f2{ 3, 8 };
f2.print();
Fraction f3{ f1 * f2 };
f3.print();
Fraction f4{ f1 * 2 };
f4.print();
Fraction f5{ 2 * f2 };
f5.print();
Fraction f6{ Fraction{1, 2} * Fraction{2, 3} * Fraction{3, 4} };
f6.print();
Fraction f7{ 0, 6 };
f7.print();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号