20-3 递归
C++中的递归函数recursive function是指能够调用自身的函数。以下是一个编写不当的递归函数示例:
#include <iostream>
void countDown(int count)
{
std::cout << "push " << count << '\n';
countDown(count-1); // countDown() calls itself recursively
}
int main()
{
countDown(5);
return 0;
}

当调用 countDown(5) 时,会打印“push 5”,并调用 countDown(4)。countDown(4) 打印“push 4”并调用 countDown(3)。countDown(3) 打印“push 3”并调用 countDown(2)。countDown(n) 调用 countDown(n-1) 的序列无限循环,实质上形成了递归版的无限循环。
在第 20.2 课栈与堆中,你已知每次函数调用都会将数据放入调用栈。由于 countDown() 函数永不返回(仅重复调用自身),这些信息永远不会从栈中弹出!最终,计算机将耗尽栈内存导致栈溢出,程序随之崩溃或终止。在作者的机器上,该程序计数倒退至-11732后终止!
作者注:
尾调用tail call是指发生在函数末尾的函数调用。具有递归尾调用的函数很容易被编译器优化为迭代(非递归)函数。在上述示例中,此类函数不会导致系统栈空间耗尽。若运行上述程序后程序无限循环,很可能就是这种情况。
递归终止条件
递归函数调用通常与普通函数调用类似。然而,上文程序展示了递归函数最重要的区别:必须包含递归终止条件,否则程序将陷入无限循环(实际上直至调用栈耗尽内存)。递归终止recursive termination条件是指当满足该条件时,递归函数将停止自我调用。
递归终止通常通过if语句实现。以下是添加终止条件(及额外输出)后的函数重构版本:
#include <iostream>
void countDown(int count)
{
std::cout << "push " << count << '\n';
if (count > 1) // termination condition
countDown(count-1);
std::cout << "pop " << count << '\n';
}
int main()
{
countDown(5);
return 0;
}
现在当我们运行程序时,countDown() 函数将首先输出以下内容:
push 5
push 4
push 3
push 2
push 1
若此时查看调用堆栈,你会看到以下内容:
countDown(1)
countDown(2)
countDown(3)
countDown(4)
countDown(5)
main()
由于终止条件的存在,countDown(1) 并未调用 countDown(0) —— 相反,“if 语句”并未执行,因此它打印出“pop 1”后便终止。此时,countDown(1) 被从栈中弹出,控制权返回至 countDown(2)。countDown(2) 从调用 countDown(1) 之后的位置继续执行,因此它打印“pop 2”后终止。递归函数调用依次从栈中弹出,直至所有 countDown 实例均被移除。
因此,该程序最终输出:
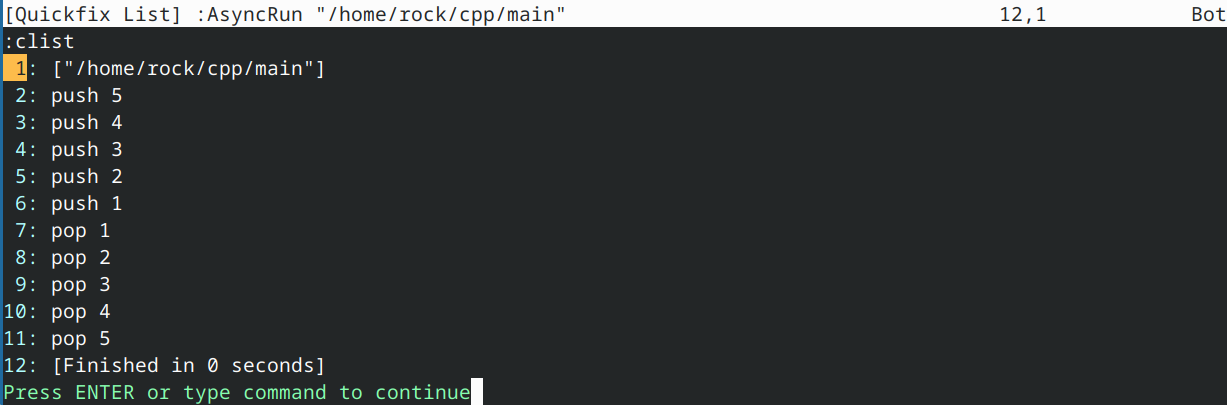
值得注意的是,“压入”输出按正向顺序发生,因为它们出现在递归函数调用之前。“弹出”输出则按逆向顺序发生,因为它们出现在递归函数调用之后——此时函数正从栈中弹出(其弹出顺序与压入顺序相反)。
一个更有用的示例
既然我们已经讨论了递归函数调用的基本机制,现在让我们看看另一个更典型的递归函数:
// return the sum of all the integers between 1 (inclusive) and sumto (inclusive)
// returns 0 for negative numbers
int sumTo(int sumto)
{
if (sumto <= 0)
return 0; // base case (termination condition) when user passed in an unexpected argument (0 or negative)
if (sumto == 1)
return 1; // normal base case (termination condition)
return sumTo(sumto - 1) + sumto; // recursive function call
}
递归程序往往难以仅凭代码外形就理解其工作原理。观察递归函数在特定参数下的调用过程通常很有启发性。那么,当我们用参数 sumto = 5 调用这个函数时,会发生什么呢?
sumTo(5) called, 5 <= 1 is false, so we return sumTo(4) + 5.
sumTo(4) called, 4 <= 1 is false, so we return sumTo(3) + 4.
sumTo(3) called, 3 <= 1 is false, so we return sumTo(2) + 3.
sumTo(2) called, 2 <= 1 is false, so we return sumTo(1) + 2.
sumTo(1) called, 1 <= 1 is true, so we return 1. This is the termination condition.
现在我们展开调用栈(在每个函数返回时将其从调用栈弹出):
sumTo(1) returns 1.
sumTo(2) returns sumTo(1) + 2, which is 1 + 2 = 3.
sumTo(3) returns sumTo(2) + 3, which is 3 + 3 = 6.
sumTo(4) returns sumTo(3) + 4, which is 6 + 4 = 10.
sumTo(5) returns sumTo(4) + 5, which is 10 + 5 = 15.
此时更容易看出,我们正在累加1到传入值之间的数字(两端都包含)。
由于递归函数仅凭代码难以理解,良好的注释尤为重要。
请注意,上述代码中我们使用值 sumto - 1 进行递归,而非 --sumto。这是因为运算符--具有副作用,若在表达式中多次对同一变量应用副作用操作,将导致未定义行为。使用 sumto - 1 可规避副作用,确保 sumto 在表达式中多次使用时安全无虞。
递归算法
递归函数通常通过先递归求解问题的子集,再修改该子解来获得最终解。在上文算法中,sumTo(value) 先求解 sumTo(value-1),再将变量 value 的值相加以求得 sumTo(value) 的解。
在许多递归算法中,某些输入会产生显而易见的输出。例如 sumTo(1) 的输出显然是 1(可心算得出),无需进一步递归。算法能直接得出结果的输入称为基准情况base case。基准情况充当算法的终止条件,通常可通过考察输入为 0、1、“ ”、“ ” 或 null 时的输出结果来识别。
斐波那契数列
斐波那契数列是最著名的数学递归算法之一。这种数列在自然界中随处可见,例如树木的分枝、贝壳的螺旋纹路、菠萝的果实排列、蕨叶的舒展卷曲,以及松果的结构。
下图展示了斐波那契螺旋:
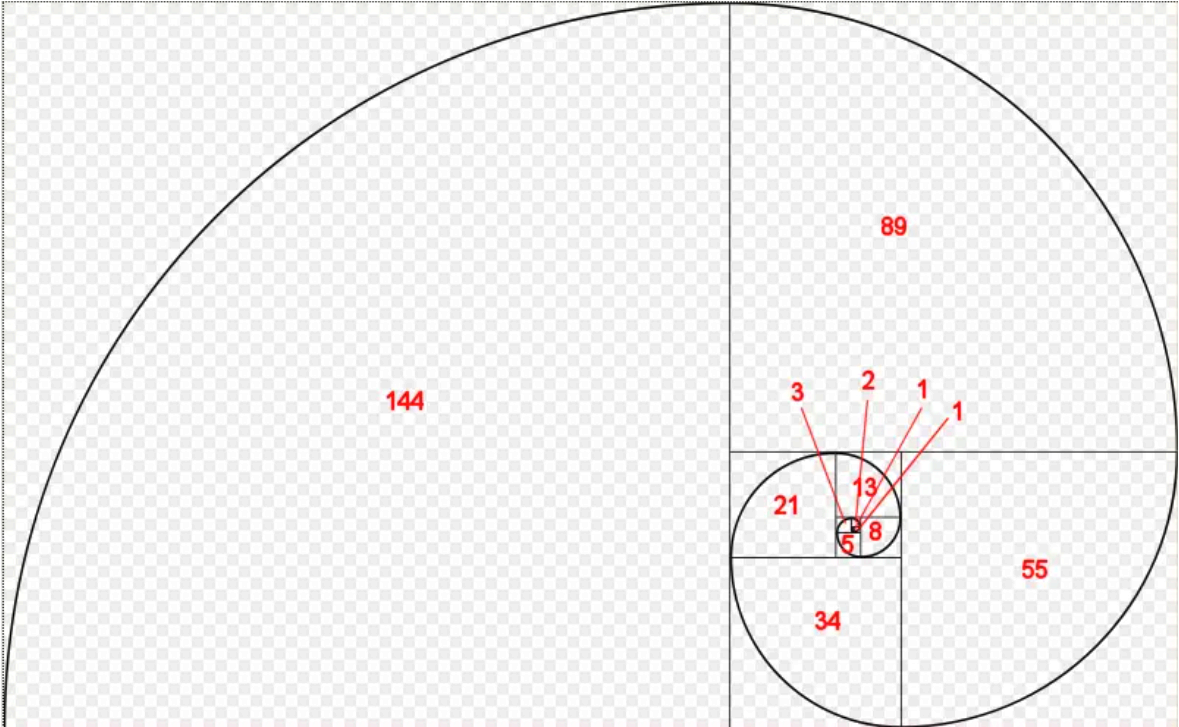
每个斐波那契数都是该数所在正方形边长的长度。
斐波那契数在数学上定义为:
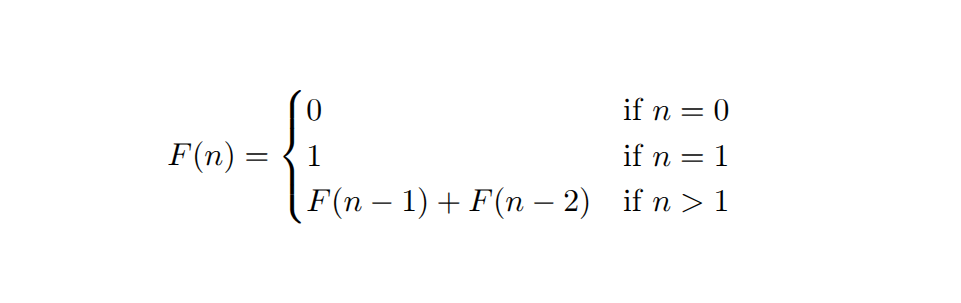
因此,编写一个(效率不高)的递归函数来计算第n个斐波那契数相当简单:
#include <iostream>
int fibonacci(int count)
{
if (count == 0)
return 0; // base case (termination condition)
if (count == 1)
return 1; // base case (termination condition)
return fibonacci(count-1) + fibonacci(count-2);
}
// And a main program to display the first 13 Fibonacci numbers
int main()
{
for (int count { 0 }; count < 13; ++count)
std::cout << fibonacci(count) << ' ';
return 0;
}
运行该程序将产生以下结果:
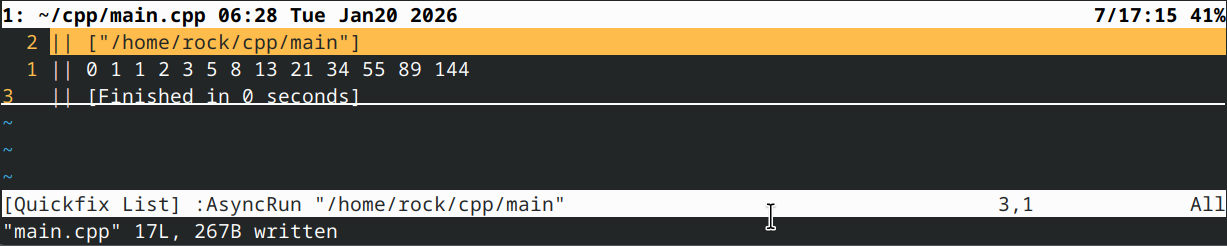
你会注意到,这些数字恰好是斐波那契螺旋图中出现的数值。
备忘录算法
上述递归斐波那契算法效率不高,部分原因在于每次调用斐波那契非基准情况都会产生两个新的斐波那契调用。这导致函数调用次数呈指数级增长(实际上,上述示例中fibonacci()被调用了1205次!)。存在若干技术手段可减少必要调用次数。其中一种称为备忘录法(memoization)的技术,通过缓存耗时函数的计算结果,当相同输入再次出现时直接返回结果。
以下是采用备忘录法的递归斐波那契算法实现:
#include <iostream>
#include <vector>
// h/t to potterman28wxcv for a variant of this code
// count is now a std::size_t to make indexing the std::vector easier
int fibonacci(std::size_t count)
{
// We'll use a static std::vector to cache calculated results
static std::vector results{ 0, 1 };
// If we've already seen this count, then use the cache'd result
if (count < std::size(results))
return results[count];
// Otherwise calculate the new result and add it
results.push_back(fibonacci(count - 1) + fibonacci(count - 2));
return results[count];
}
// And a main program to display the first 13 Fibonacci numbers
int main()
{
for (int count { 0 }; count < 13; ++count)
std::cout << fibonacci(static_cast<std::size_t>(count)) << ' ';
return 0;
}

此备忘录版本执行了35次函数调用,远优于原始算法的1205次调用。
递归与迭代
关于递归函数常被问及的问题是:“既然许多相同任务可通过迭代(使用for循环或while循环)实现,为何还要使用递归函数?”事实上,递归问题总能用迭代方式解决——但对于非平凡问题,递归版本往往更易编写(且更易阅读)。例如,虽然可以迭代实现斐波那契函数,但实现难度更高!(不妨尝试!)
迭代函数(使用for循环或while循环)几乎总是比递归函数更高效。这是因为每次函数调用都会产生栈帧压入/弹出的开销,而迭代函数能避免这种开销。
但这并非意味着迭代函数永远是最佳选择。有时递归实现能带来更简洁易懂的代码,即使存在额外开销,其可维护性优势也完全值得——尤其当算法无需多次递归即可求解时。
总体而言,当以下条件基本成立时,递归是优选方案:
- 递归代码实现更为简洁
- 递归深度可控(例如不存在导致递归深入十万层的输入)
- 迭代版本需管理数据栈
- 该代码段对性能要求不高
但若递归算法更易实现,可先采用递归方案,后续再优化为迭代算法
最佳实践:
除递归确有优势的情况外,通常优先选择迭代而非递归。
测验时间
1.整数 N 的阶乘(记作 N!)定义为 1 到 N 之间所有数字的乘积(0! = 1)。编写一个名为 factorial 的递归函数,返回输入数的阶乘。用前 7 个阶乘测试该函数。
提示:注意 (x * y) = (y * x),因此1到N之间所有数字的乘积等于N到1之间所有数字的乘积。
显示解决方案
#include <iostream>
int factorial(int n)
{
if (n <= 0)
return 1;
return factorial(n - 1) * n;
}
int main()
{
for (int count { 0 }; count < 7; ++count)
std::cout << factorial(count) << '\n';
}
编写递归函数,接受整数输入并返回该整数中每个数字的和(例如357 = 3 + 5 + 7 = 15)。请输出输入93427的答案(即25)。假设输入均为正数。
显示解决方案
#include <iostream>
int sumDigits(int x)
{
if (x < 10)
return x;
return sumDigits(x / 10) + x % 10;
}
int main()
{
std::cout << sumDigits(93427);
}
3a) 此题稍具挑战性。编写程序引导用户输入正整数,并通过递归函数输出该数的二进制表示。需运用O.4课时方法1——整数二进制与十进制转换。
提示:采用方法1时需按位倒序输出,因此打印语句应置于递归调用之后。
显示解决方案
#include <iostream>
// h/t to reader Gapo for this solution
void printBinary(int x)
{
// Termination case
if (x == 0)
return;
// Recurse to the next bit
printBinary(x / 2);
// Print out the remainders (in reverse order)
std::cout << x % 2;
}
int main()
{
int x;
std::cout << "Enter a positive integer: ";
std::cin >> x;
printBinary(x);
}
3b) 附加题:修改3a的代码,处理用户输入0或负数的情况。
以下为示例输出(假设使用32位整数):
Enter an integer: -15
11111111111111111111111111110001
提示:您的printBinary()函数实际上无需处理负数。若传入与负数二进制表示相同的正数,它将输出正确结果。
显示提示
提示:有符号与无符号之间的转换不会改变二进制表示形式,仅改变值的解释方式。例如,有符号整数 -15 的二进制表示为 11111111111111111111111111110001,与无符号整数 4294967281 完全相同。
显示提示
提示:有符号值可以是正数或负数,但无符号值永远是正数……
显示解决方案
// h/t to reader Donlod for this solution
#include <iostream>
void printBinary(unsigned int n)
{
if (n > 1) // we only recurse if n > 1, so this is our termination case for n == 0
{
printBinary(n / 2);
}
std::cout << n % 2;
}
int main()
{
int x{};
std::cout << "Enter an integer: ";
std::cin >> x;
printBinary(static_cast<unsigned int>(x));
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号