17-12 多维C风格数组
以井字棋为例。该游戏的标准棋盘为3×3网格,玩家轮流放置“X”和“O”符号,最先连成三格者获胜。
虽然可以将棋盘数据存储为9个独立变量,但当某个元素存在多个实例时,使用数组更为合理:
int ttt[9]; // a C-style array of ints (value 0 = empty, 1 = player 1, 2 = player 2)
这定义了一个C风格的数组,包含9个元素,它们在内存中按顺序排列。我们可以想象这些元素被布局成单行数值,如下所示:
// ttt[0] ttt[1] ttt[2] ttt[3] ttt[4] ttt[5] ttt[6] ttt[7] ttt[8]
数组的维度是指选择一个元素所需的索引数量。仅包含单一维度的数组称为单维数组single-dimensional array或一维数组one-dimensional array(有时简称为1d数组1d array)。上文中的ttt就是一维数组的示例,因为元素只需单个索引即可选取(例如ttt[2])。
但请注意,这个一维数组与我们二维的井字棋棋盘差异较大。我们可以做得更好。
二维数组
在之前的课程中,我们提到数组的元素可以是任意对象类型。这意味着数组的元素类型可以是另一个数组!定义这样的数组很简单:
int a[3][5]; // a 3-element array of 5-element arrays of int
数组的数组称为二维数组(有时简称为2d数组),因为它具有两个下标。
对于二维数组,通常将第一个(左侧)下标视为选择行,第二个(右侧)下标视为选择列。概念上,我们可以将这个二维数组想象成如下布局:
// col 0 col 1 col 2 col 3 col 4
// a[0][0] a[0][1] a[0][2] a[0][3] a[0][4] row 0
// a[1][0] a[1][1] a[1][2] a[1][3] a[1][4] row 1
// a[2][0] a[2][1] a[2][2] a[2][3] a[2][4] row 2
要访问二维数组的元素,我们只需使用两个下标:
a[2][3] = 7; // a[row][col], where row = 2 and col = 3
因此,对于井字棋棋盘,我们可以定义如下二维数组:
int ttt[3][3];
现在我们拥有一个3×3的元素网格,可以轻松地通过行索引和列索引进行操作!
多维数组
超过1维度的数组称为多维数组multidimensional arrays。
C++ 甚至支持维度超过 2 的多维数组:
int threedee[4][4][4]; // a 4x4x4 array (an array of 4 arrays of 4 arrays of 4 ints)
例如,《我的世界》中的地形被划分为16×16×16的方块(称为区块段)。
支持维度高于3的数组,但较为罕见。
二维数组在内存中的布局方式
内存是线性的(一维的),因此多维数组实际上以元素的顺序列表形式存储。
以下数组在内存中有两种可能的存储方式:
// col 0 col 1 col 2 col 3 col 4
// [0][0] [0][1] [0][2] [0][3] [0][4] row 0
// [1][0] [1][1] [1][2] [1][3] [1][4] row 1
// [2][0] [2][1] [2][2] [2][3] [2][4] row 2
C++采用行优先顺序,即元素按行顺序row-major order依次存放在内存中,从左到右、从上到下排列:
[0][0] [0][1] [0][2] [0][3] [0][4] [1][0] [1][1] [1][2] [1][3] [1][4] [2][0] [2][1] [2][2] [2][3] [2][4]
其他一些语言(如Fortran)采用列优先顺序,元素按列顺序column-major order依次存入内存,从上到下、从左到右排列:
[0][0] [1][0] [2][0] [0][1] [1][1] [2][1] [0][2] [1][2] [2][2] [0][3] [1][3] [2][3] [0][4] [1][4] [2][4]
在 C++ 中,初始化数组时,元素按行优先顺序进行初始化。遍历数组时,按元素在内存中的布局顺序访问最为高效
初始化二维数组
初始化二维数组最简便的方法是使用嵌套大括号,其中每组数字代表一行:
int array[3][5]
{
{ 1, 2, 3, 4, 5 }, // row 0
{ 6, 7, 8, 9, 10 }, // row 1
{ 11, 12, 13, 14, 15 } // row 2
};
尽管某些编译器允许省略内部大括号,但我们强烈建议您为提高代码可读性而保留它们。
使用内部大括号时,缺失的初始化项将采用值初始化:
int array[3][5]
{
{ 1, 2 }, // row 0 = 1, 2, 0, 0, 0
{ 6, 7, 8 }, // row 1 = 6, 7, 8, 0, 0
{ 11, 12, 13, 14 } // row 2 = 11, 12, 13, 14, 0
};
初始化的多维数组可以省略(仅限)最左侧的长度规格:
int array[][5]
{
{ 1, 2, 3, 4, 5 },
{ 6, 7, 8, 9, 10 },
{ 11, 12, 13, 14, 15 }
};
在这种情况下,编译器可以根据初始化项的数量计算出最左侧的长度。
不允许省略非最左侧的维度:
int array[][]
{
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 }
};

与普通数组类似,多维数组仍可初始化为0,如下所示:
int array[3][5] {};
二维数组与循环
对于一维数组,我们可以使用单个循环遍历数组中的所有元素:
#include <iostream>
int main()
{
int arr[] { 1, 2, 3, 4, 5 };
// for-loop with index
for (std::size_t i{0}; i < std::size(arr); ++i)
std::cout << arr[i] << ' ';
std::cout << '\n';
// range-based for-loop
for (auto e: arr)
std::cout << e << ' ';
std::cout << '\n';
return 0;
}

对于二维数组,我们需要两个循环:一个用于选择行,另一个用于选择列。
使用两个循环时,还需确定哪个循环作为外层循环,哪个作为内层循环。按元素在内存中的排列顺序访问效率最高。由于C++采用行优先顺序,行选择器应作为外层循环,列选择器应作为内层循环。
#include <iostream>
int main()
{
int arr[3][4] {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 }};
// double for-loop with indices
for (std::size_t row{0}; row < std::size(arr); ++row) // std::size(arr) returns the number of rows
{
for (std::size_t col{0}; col < std::size(arr[0]); ++col) // std::size(arr[0]) returns the number of columns
std::cout << arr[row][col] << ' ';
std::cout << '\n';
}
// double range-based for-loop
for (const auto& arow: arr) // get each array row
{
for (const auto& e: arow) // get each element of the row
std::cout << e << ' ';
std::cout << '\n';
}
return 0;
}
二维数组示例
让我们来看一个二维数组的实际应用示例:
#include <iostream>
int main()
{
constexpr int numRows{ 10 };
constexpr int numCols{ 10 };
// Declare a 10x10 array
int product[numRows][numCols]{};
// Calculate a multiplication table
// We don't need to calc row and col 0 since mult by 0 always is 0
for (std::size_t row{ 1 }; row < numRows; ++row)
{
for (std::size_t col{ 1 }; col < numCols; ++col)
{
product[row][col] = static_cast<int>(row * col);
}
}
for (std::size_t row{ 1 }; row < numRows; ++row)
{
for (std::size_t col{ 1 }; col < numCols; ++col)
{
std::cout << product[row][col] << '\t';
}
std::cout << '\n';
}
return 0;
}
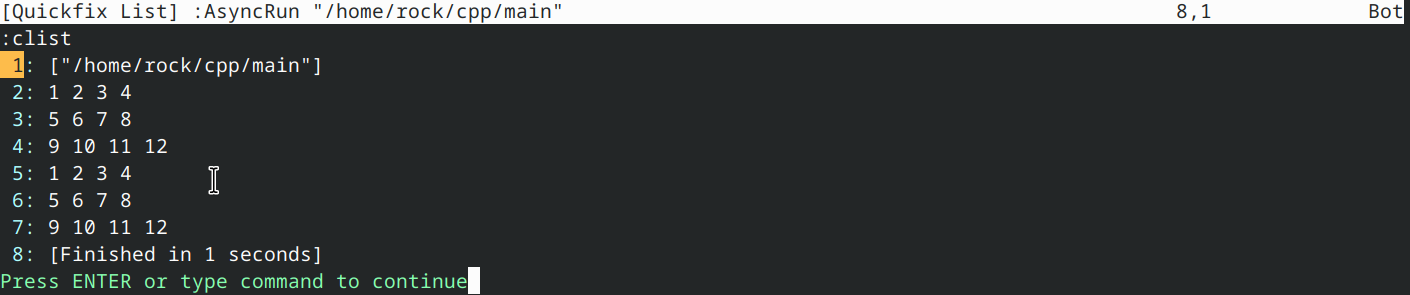
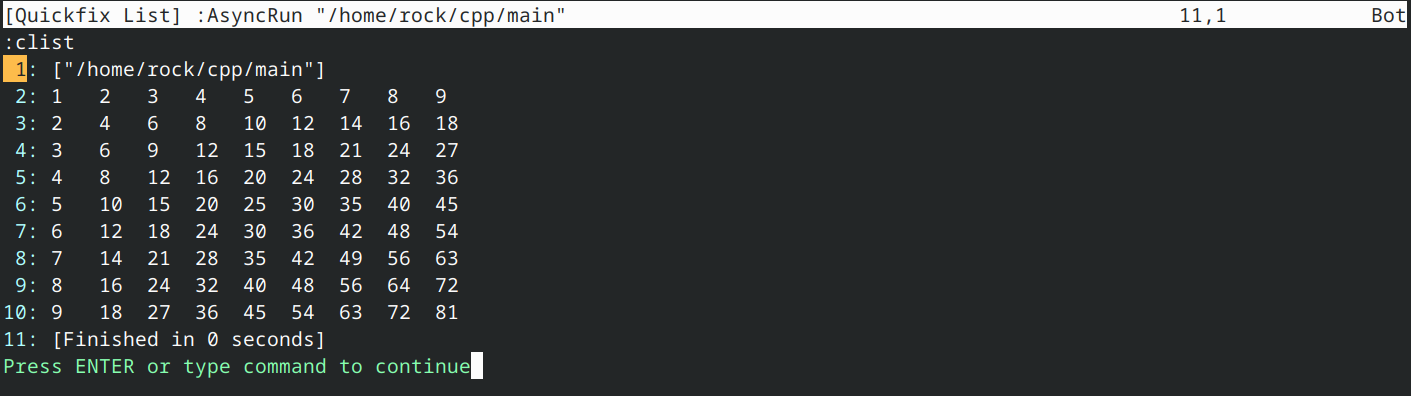
该程序计算并打印1到9(含)之间所有值的乘法表。请注意,打印表格时for循环从1开始而非0。此设计旨在省略打印0列和0行——否则只会显示一串0!输出如下:
笛卡尔坐标系与数组索引
在几何学中,笛卡尔坐标系常用于描述物体的位置。二维空间中存在两条坐标轴,通常命名为“x”轴和“y”轴。“x”轴代表水平方向,“y”轴代表垂直方向。
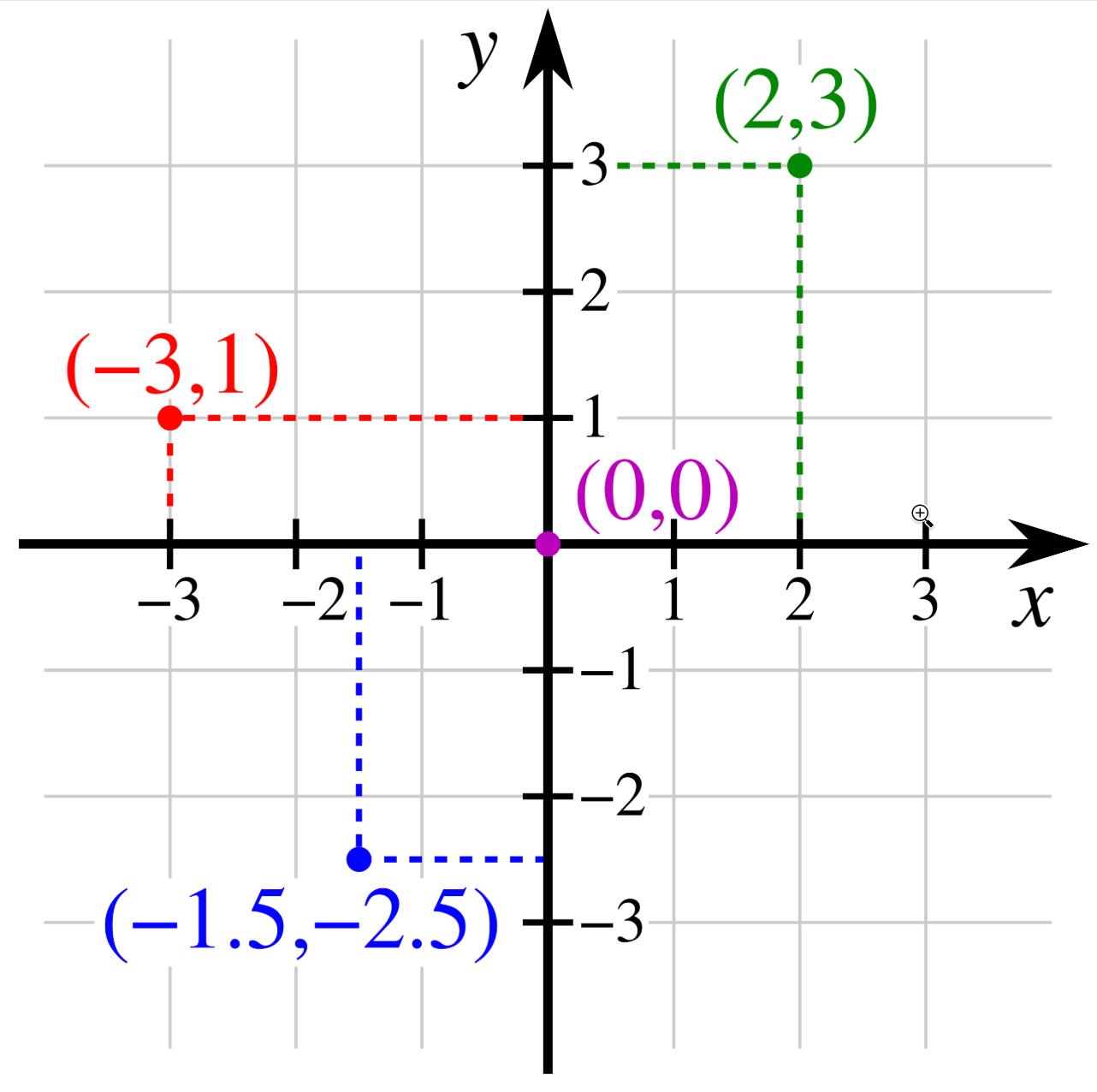
在二维空间中,物体的笛卡尔坐标位置可描述为{x, y}元组,其中x坐标和y坐标分别表示物体相对于x轴的右偏距离和相对于y轴的上方距离。有时y轴会发生翻转(此时y坐标表示物体相对于y轴的下方距离)。
现在让我们看看C++中的二维数组布局:
// col 0 col 1 col 2 col 3 col 4
// [0][0] [0][1] [0][2] [0][3] [0][4] row 0
// [1][0] [1][1] [1][2] [1][3] [1][4] row 1
// [2][0] [2][1] [2][2] [2][3] [2][4] row 2
这也是一种二维坐标系,其中元素的位置可描述为[行][列](其中列轴方向被翻转)。
虽然这些坐标系各自独立时都相当容易理解,但从笛卡尔坐标系{ x, y }转换为数组索引[行][列]的过程却有些违背直觉。
关键在于:笛卡尔坐标系中的x坐标对应数组索引系统中选取的列,而y坐标则对应选取的行。因此{ x, y }笛卡尔坐标转换为[y][x]数组坐标时,方向恰好与直觉相反!
由此形成的二维循环结构如下所示:
for (std::size_t y{0}; y < std::size(arr); ++y) // outer loop is rows / y
{
for (std::size_t x{0}; x < std::size(arr[0]); ++x) // inner loop is columns / x
std::cout << arr[y][x] << ' '; // index with y (row) first, then x (col)
请注意,在此情况下,我们以 a[y][x] 的形式对数组进行索引,这可能与你预期的字母顺序相反。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号