深度学习-手写数字图

🧠 神经网络训练流程（MLP）

          [1. 输入层]
            784个像素点
                 │
                 ▼
╭────────────────────────────╮
│ 1️⃣ Forward Propagation 初始值│
│ 输入 → 加权和 → 激活函数 → 输出预测 ŷ │   （训练或预测步骤）
╰────────────────────────────╯
                 │
                 ▼
╭────────────────────────────╮
│ 2️⃣ Loss Calculation         │
│ 计算 ŷ 和真实 y 的差异（损失函数 L） │
╰────────────────────────────╯
                 │
                 ▼
╭────────────────────────────╮
│ 3️⃣ Backpropagation         │
│ 误差反向传播，计算每个参数的梯度    │
╰────────────────────────────╯
                 │
                 ▼
╭────────────────────────────╮
│ 4️⃣ Update Parameters        │
│ 使用优化器（如SGD/Adam）更新 W 和 b │
╰────────────────────────────╯
                 │
                 ▼
╭────────────────────────────╮
│ 5️⃣ Repeat / Epochs          │
│ 对整个数据集重复训练若干轮         │
╰────────────────────────────╯
                 ▲
                 │
             （循环）

多层感知器 (MLP) 神经网络结构

多层感知器（MLP）是一种前馈神经网络，其基本结构由三大部分构成：输入层、隐藏层和输出层。接下来，我们以手写数字识别为例，介绍 MLP 如何利用图像的像素信息来进行分类。

图像到矩阵的转换

手写数字图像通常为 28×28 像素，每个像素携带一个灰度值（范围 0-1，从黑到白）。我们将图像的 28×28 个像素点展开成一个 784 维的向量，即：

  • 原始图像：28 x 28 像素
  • 向量化：1行 784列

这样，每个像素点就对应着向量中的一个元素，形成了整个图像的空间特征表示。

手写数字图到矩阵转换过程

转换为784维度向量：{0.1，0.5...0.45}

神经网络的三层结构

MLP 神经网络主要分为以下三层：

  1. 输入层
    输入层由 784 个神经元构成，每个神经元对应手写数字图像中的一个像素点。这一层负责接收原始数据，不涉及权重更新，仅做数据的拆分与预处理。

  2. 隐藏层
    隐藏层可以包含一层或多层神经元，用于提取和组合输入数据中的特征。在我们的例子中，假设有两层隐藏层：

    • 第一隐藏层包含 16 个神经元，
    • 第二隐藏层也包含 16 个神经元，

    每个神经元的激活值受上一层所有神经元输出的线性组合影响，经过非线性激活函数（如 ReLU 或 Sigmoid）后传递到下一层。隐藏层的主要作用是对输入数据进行复杂的特征抽象和组合，从而使网络能够捕捉到输入中的深层模式和结构。

  3. 输出层
    输出层用于给出最终的分类结果。在手写数字识别中，输出层通常由 10 个神经元组成，对应数字 0 到 9 的概率分布。输出层的结果会与真实标签进行比较，利用监督信号对整个网络进行训练和调整。

神经网络分层结构
多层感知MLP神经网络激活传导示意

图 2：输入层、隐藏层和输出层的神经网络结构示意图。图中每层节点间的连接表示激活值的传递过程。

神经元之间的线性代数运算

在神经网络中，每个神经元的计算可以归结为一系列线性代数运算，主要包括矩阵乘法和加法。具体来说：

  • 输入层到第一隐藏层
    输入数据（784 维向量）与权重矩阵（尺寸为 784×16）相乘，并加上偏置向量，得到第一隐藏层的激活值。
  • 第一隐藏层到第二隐藏层
    第一隐藏层的输出与权重矩阵（尺寸为 16×16）相乘，并加上偏置，得到第二隐藏层的激活值。
  • 第二隐藏层到输出层
    第二隐藏层的输出与权重矩阵（尺寸为 16×10）相乘，并加上偏置，生成输出层的预测结果。

计算参数总量为：

  • 输入层到第一隐藏层：784 x 16
  • 第一隐藏层到第二隐藏层：16 x 16
  • 第二隐藏层到输出层：16 x 10

因此，总参数量为：784×16 + 16×16 + 16×10 = 13002

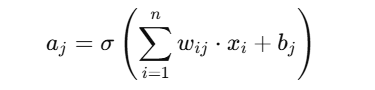
一个神经元激活值计算
图 3：神经网络中每个神经元计算公式，展示了矩阵乘法和加法的过程。
参数解析：𝜎-激活函数，b-偏置值，w-当前神经元权重矩阵，x-上一层输入向量

项目 说明 是否需要训练
( x_i ) 输入值（例如图像像素） ✅ 确定的，由数据提供
( w_{ij} ) 权重，表示输入 ( x_i ) 到当前神经元的连接强度 ❗需要训练
( b_j ) 偏置项，调整输出位置 ❗需要训练
( \sigma(\cdot) ) 激活函数，例如 ReLU/Sigmoid ✅ 固定函数
( a_j ) 当前神经元的输出 ✅ 计算得到的结果

✅：确定的/给定的
❗：训练得到的参数（也叫“模型参数”）

  • 输入层 负责数据预处理和向量化。
  • 隐藏层 通过多层非线性变换提取特征。
  • 输出层 根据提取到的特征进行分类，生成与真实标签对比的结果，用于网络训练。

当然可以，以下是根据你提供内容整理和补充后的 Markdown 版本，重点对术语表述、逻辑层次和公式清晰度做了增强，并补充了几个关键细节：

多层感知 MLP 神经网络 - 梯度下降法（Gradient Descent）

Cost（Loss）函数的定义与意义

代价函数（Cost Function，也称为损失函数 Loss）是用于衡量神经网络在整个训练集上的预测输出与真实标签之间差异的一个函数。
由于代价函数在高维空间中非常复杂，梯度下降不一定每次都能找到全局最小，有一些方法来尽量避免陷入局部最小值，比如：优化算法等

  • 神经网络内部有 13000多个参数（权重 + 偏置）。
  • 每个参数组合都会得到一组预测结果，代价函数给这组预测打分。
  • 目标是让这个“评分”尽可能低——也就是说，让网络的预测越准确越好。

常见代价函数：
对分类任务，通常使用 均方误差（MSE） 或 交叉熵（Cross Entropy）。

例如，均方误差：

[Cost = 1/2n * sum_{x} || `y^(x) - y^(x) ||^2]

  • ( `y} )：模型预测输出（激活值）例如
  • ( y )：真实标签（目标输出）例如标签为3
  • ( n )：样本数

梯度下降（Gradient Descent）的核心思想

梯度告诉我们：每个参数的调整方向和幅度，使得代价函数下降最快。

梯度下降的步骤：

  1. 初始化参数（权重和偏置）为随机值（通常在一个小范围内均匀采样）。

  2. 计算当前模型在训练数据上的 Cost 值。

  3. 计算 Cost 关于每个参数的梯度

  4. 反向传播算法（Backpropagation） 用于高效地计算每个参数的偏导数。

  5. 更新参数（按负梯度方向）：

  • ( \eta )：学习率（learning rate），控制步长大小。

为什么使用连续激活函数？

  • 若激活函数是离散的（如生物神经元“开/关”），则导数几乎为0或不存在，梯度下降将无法工作。
  • 因此，我们使用 连续且可微分的激活函数（如 Sigmoid, ReLU, Tanh），保证代价函数整体光滑，便于迭代优化。

为什么训练集要有通用特征？

  • 当训练数据是真实有效的手写数字时，图像中包含某些通用结构（如圆圈、竖线、弯钩），模型可以通过梯度下降快速学习这些特征。
  • 而如果标签是随机的，模型无法找到一致的结构，代价函数表面可能杂乱无章，训练效果就会很差。

训练的终极目标

训练神经网络的实质：让代价函数尽可能小，即：

  • 每张图像的预测尽可能接近真实标签；
  • 参数组合越来越“聪明”，能够捕捉输入数据的通用规律。

多层感知器 (MLP) 反向传播（Backpropagation）

反向传播算法是神经网络训练的核心，它告诉我们：每个参数（权重和偏置）应该如何调整，才能让模型更好地预测结果。

梯度的含义

  • 代价函数的梯度向量告诉我们：每个参数对代价函数的影响程度。
  • 换句话说，梯度的每一项表示：若该参数微调一点，Cost 会增加还是减少，变化多大。

神经元的参数

对于一个神经元来说，有两个核心参数：

  • **权重 w **：来自上一层的每个神经元都有一个权重；
  • **偏置 b **：控制这个神经元本身的激活门槛。

例如，如果两个输入神经元分别连接当前神经元，权重为：

  • w_1 = 3.2 ， w_2 = 0.1 ，
    则说明第一个神经元对当前神经元的影响是第二个的 32 倍。

反向传播的核心流程

  1. 前向传播（Forward Pass）
    输入样本通过神经网络计算出预测值 `y 。

  2. 误差计算（Loss）
    比较 y 和真实值 y ，计算损失函数 L(y, y) 。

  3. 反向传播误差（Backward Pass）
    从输出层开始，逐层向前传播误差，计算每个神经元输出的误差对其输入权重和偏置的梯度：

    • 输出层误差：由预测和真实标签的差值决定；
    • 中间层误差：由下一层误差“反推”而来。

  4. 累计每个样本对权重和偏置的修改建议
    每个训练样本会“建议”如何修改每个参数；
    将所有样本的修改量 平均，得到最终的梯度估计。

  5. 更新参数（梯度下降）
    使用学习率 eta 沿梯度方向更新参数：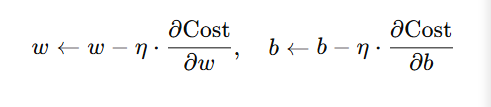

    参数更新

随机梯度下降（Stochastic Gradient Descent, SGD）

如果训练集很大，计算完整梯度太慢，我们就使用 随机梯度下降：

  • 每次只使用一个样本或一小批样本（mini-batch）计算梯度；
  • 更新参数后马上前进到下一个样本；
  • 优点：更快收敛、更具探索性、避免陷入局部最小值；
  • 常见优化器（如 Adam、RMSProp）都是 SGD 的改进版本。

总结一句话：

反向传播就是：先算出每一层误差，然后逐层反向计算每个参数对误差的贡献，最终用梯度下降法来调整权重和偏置，从而最小化整体代价函数。

总结

手写数字图识别是通过多层感知器（MLP）神经网络实现的：将一张 28x28 像素的灰度图像展平成784维输入向量，送入神经网络的输入层，经过一层或多层隐含层的线性加权与非线性激活处理，最终输出层生成10个神经元，对应0~9的数字类别。训练过程中，先通过前向传播计算输出，再利用损失函数衡量预测值与真实标签的误差，接着通过反向传播计算梯度，最后用梯度下降法不断优化权重和偏置，使得网络逐步学会从输入图像中提取数字特征，实现对手写数字的准确分类。

posted @ 2025-04-07 12:19  代码世界faq  阅读(51)  评论(0)    收藏  举报