一.所花时间
0.5h
二.代码量
30行
三.博客量
1篇
四.了解到的知识点
实验二:最速下降法程序设计
一、实验目的
通过最速下降法的程序设计,为今后的约束优化方法的学习和编程奠定基础;掌握负梯度方向的定义和最速下降法的迭代公式 ;通过此次实验,进一步巩固最速下降法的基本原理和思想。
二、实验内容
(1)求解无约束优化问题: ;
(2)终止准则取 ;
(3)完成最速下降法(负梯度法)的MATLAB编程、调试;
(4)要求选取多个不同的初始点,并给出迭代次数,最优函数值等相关信息,有能力的同学尝试画出最优值随迭代次数变化的曲线图;
(5)按照模板撰写实验报告,要求规范整洁。
三、算法步骤、代码、及结果
1. 算法步骤
(1)给出初始点x 0,置iter=0,最大迭代次数max_iter=10000,精度e=1e-6,目标 函数f及其梯度grad
(2)若终止条件满足(| | f | | < e),则迭代停止
(3)计算d k = −grad
(4)在d k方向上利用一维精确线性搜索Amrijo搜索求步长ak
(5)x k + 1 = x k + α k d k , k = k + 1,转步骤2
2.代码
function f=fun(x)
f= (x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4;
function gf=gfun(x)
gf = [2*(x(1)+10*x(2))+40*(x(1)-x(4))^3; 20*(10*x(2)+x(1))+4*(x(2)-2*x(3))^3; 10*(x(3)-x(4))-8*(x(2)-2*x(3))^3; -10*(x(3)-x(4))-40*(x(1)-x(4))^3];
function [k,x,val] = grad(fun,gfun,x0_list,epsilon)
%功能:用最速下降法求解无约束优化问题
%输入:funf,gfun分别是目标函数和梯度,x0是初始点,epsilon是容许误差
%输出:x,val分别是近似最优解和最优值,k是迭代次数
maxk=10000; %最大迭代次数
value = zeros(maxk, 1);
for i = 1:length(x0_list)-1
x0 = x0_list(:,i);
beta=0.5; sigma=0.4;
k=0;
fprintf('初始点 (%g; %g; %g; %g)\n', x0(1), x0(2), x0(3), x0(4));
while(k<maxk)
gk=feval(gfun,x0); %计算梯度
dk=-gk;
if(norm(gk)<epsilon), break; end %检验终止准则
m=0; mk=0;
%用Amrijo搜索技术确定步长
while(m<20) %最大迭代次数
if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk)
mk=m; break;
end
m=m+1;
end
x0=x0+beta^mk*dk;
k=k+1;
value(k,1)=feval(fun,x0);
end
x=x0;
val=feval(fun,x0);
fprintf('迭代次数: %d\n', k);
fprintf('最优点: (%g; %g; %g; %g)\n', x(1), x(2), x(3), x(4));
fprintf('最优函数值: %g\n', val);
fprintf('\n');
% 迭代曲线图
figure;
plot(value);
title('迭代曲线');
xlabel('迭代次数');
ylabel('最优值');
end
% 命令行输入
% x0=[-1,-2,3; 1,7,10; 3,-4,5; 3,6,4];
% grad('fun','gfun',x0,1e-6);3.结果
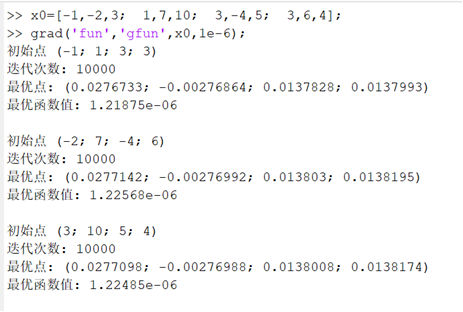
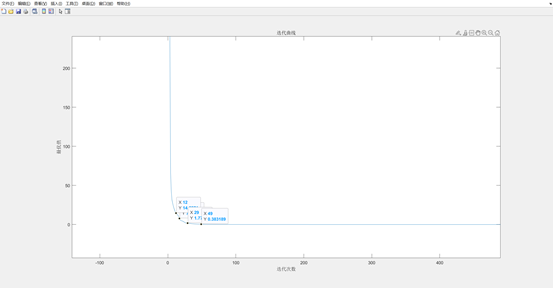
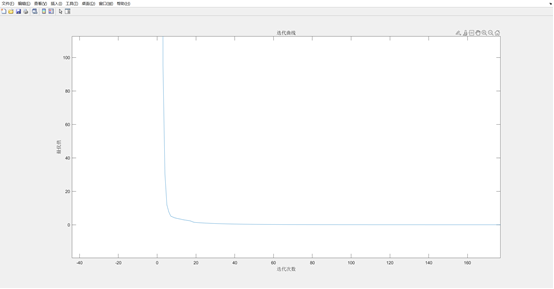
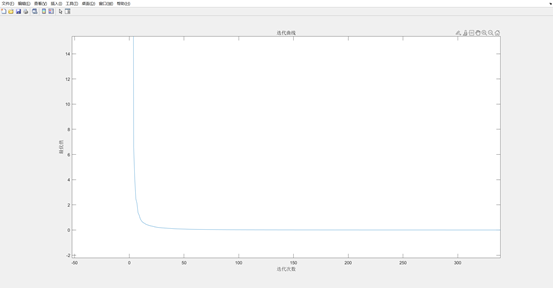




 浙公网安备 33010602011771号
浙公网安备 33010602011771号