洛谷[过河卒]

棋盘上 AA 点有一个过河卒，需要走到目标 BB 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 CC 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，AA 点 (0, 0)(0,0)、BB 点 (n, m)(n,m)，同样马的位置坐标是需要给出的。

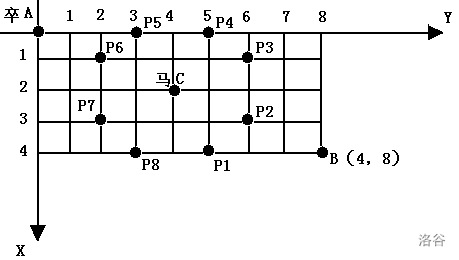
现在要求你计算出卒从 AA 点能够到达 BB 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 BB 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1复制

6 6 3 3

输出 #1复制

6

说明/提示

对于 100 \%100% 的数据，1 \le n, m \le 201≤n,m≤20，0 \le0≤ 马的坐标 \le 20≤20。

 

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#define MAXL 24
using namespace std;
long long world[MAXL][MAXL]{0}; //二维数组初始化
long long max_4(long long a, long long b, long long c, long long d)
{
    return max(max(a, b), max(c, d));
}
long long num_up(long long a, long long b) //假设只能从上面走下来
{
    return (world[a - 1][b]);
}
long long num_left(long long a, long long b) //假设只能从左边走出来
{
    return (world[a][b - 1]);
}
long long num_full(long long a, long long b) //假设可以从俩边走出来
{
    return (world[a - 1][b] + world[a][b - 1]);
}
long long horse_next[8][2] = {
    {1, -2},
    {2, -1},
    {2, 1},
    {1, 2},
    {-1, 2},
    {-2, 1},
    {-2, -1},
    {-1, -2},
};
void look()
{
    for (long long l = 0; l < MAXL; l++)
    {
        for (long long r = 0; r < MAXL; r++)
        {
            printf("%-5d", world[l][r]);
        }
        printf("\n");
    }
}
long long A, B, X, Y; //终点的坐标(a,b)，马的坐标(x,y)
int main()
{
    cin >> A >> B >> X >> Y;
    X++, Y++, B++, A++; //这些玩意全部要++因为我在最外面弄了一圈0

    world[1][1] = 1; //初始赋值
    world[2][1] = 1;
    world[1][2] = 1;
    /*
    for (int i = 2; i <= A; i++)
    {
        world[i][1] = 1;
    }
    for (int i = 2; i <= B; i++)
    {
        world[1][i] = 1;
    }*/
    //look();
    //准备进入神奇的dp之旅
    world[X][Y] = -0x3f3f3f3f; //赋值成负无穷
    for (long long i = 0; i < 8; i++)
    {
        if (X + horse_next[i][0] >= 1 && X + horse_next[i][0] <= A && Y + horse_next[i][1] >= 1 && Y + horse_next[i][1] <= B)
            world[X + horse_next[i][0]][Y + horse_next[i][1]] = -0x3f3f3f3f;
    }
    for (long long l = 1; l <= A; l++)
    {
        for (long long r = 1; r <= B; r++)
        {
            if (world[l][r] >= 0) //排除那个点不能走的情况
            {
                world[l][r] = max_4(num_up(l, r), num_left(l, r), num_full(l, r), world[l][r]);
            }
        }
    }
    //look();
    cout << world[A][B] << endl;
    return 0;
}

试过DFS会超时，这里有一个坑点；

就是应该先初始化好world[0][1],world[1][0]world[0][0](虽然实际上他们在二维数组中都加了1)，再放马

一个小技巧就是，可以在二维数组的外面放上一圈0