P2181 对角线 洛谷

 

对于一个 nn 个顶点的凸多边形，它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。

例如，66 边形：

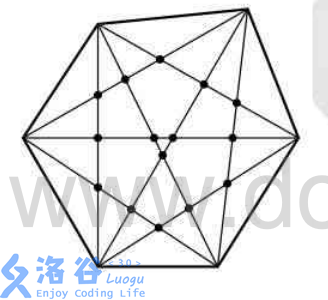
输入格式

输入只有一行一个整数 nn，代表边数。

输出格式

输出一行一个整数代表答案。

输入输出样例

输入 #1复制

3

输出 #1复制

0

输入 #2复制

6

输出 #2复制

15

说明/提示

数据规模与约定

• 对于 50 \%50% 的数据，保证 3 \leq n \leq 1003≤n≤100。
• 对于 100 \%100% 的数据，保证 3 \leq n \leq 10^53≤n≤105。

 

 

#include <stdio.h>

int main()

{

    unsigned long long n;

    scanf("%lld", &n);

    if (n <= 3)  //特殊情况当 n <= 3 时实际上是没有对角线的交点的

        printf("0\n");

    else

        printf("%lld\n", n * (n - 1) / 2 * (n - 2) / 3 * (n - 3) / 4);

    return 0;

}

 

这是一个数学问题

这个作者已经说的很好了

我们可以发现，两条不平行对角线才会有一个交点，同时，两条对角线又确定了一个四边形，也就是确定了4个顶点。如果我们确定了4个顶点的组合方式，我们也就能确定有多少个四边形，进而确定有多少个对角线交点。用排列组合的计算公式就是

即N*(N-1)(N-2)(N-3)/(4321)
考虑到如果初始N很大时，上面结果会超级大，可以改写成N(N-1)/2*(N-2)*/3(N-3)/4

那为什么这样一定是对的呢？难道不会因为除不尽却向下取整而导致错误吗？

事实上是一定除得尽的

首先n和n-1一定有一个是２的倍数，因此２可以除尽，

同理n,n-1,n-2中一定有一个是３的倍数，因此３可以除尽（除掉２只会消除因数２而对３没有影响）
————————————————
版权声明：本文为CSDN博主「lovewonder」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lovewonder/article/details/104550265/