剑指offer：二叉搜索树与双向链表

题意描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

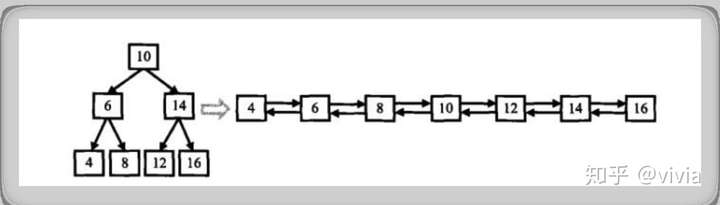
题目示例

解题思路

一、递归

在二叉搜索树中，左子节点小于父节点，右子节点大于父节点。如果要转为双向链表，要对二叉树进行中序遍历，遍历结果就是链表中节点的顺序。将二叉树分成三部分，根节点、左子树、右子树，将左子树的最大值与根节点连接，右子树的最小值与二叉树连接。

    public class Solution {
        private TreeNode head = null;	//保存头节点
        private TreeNode pre = null;	//保存当前节点的上一个节点
        public TreeNode Convert(TreeNode pRootOfTree) {
            con(pRootOfTree);
            return head;	//返回头节点
        }
        public void con(TreeNode root){
            if(root == null) return;	//根节点为空
            con(root.left);		//向左递归
            if(head == null){	//说明是当前子树的最左子节点
                head = root;	
                pre = root;		
            }else {
                pre.right = root;	//连接root
                root.left = pre;	
                pre = root;		    //更新pre为当前子树的root
            }
            con(root.right);	//向右递归
        }
    }

二、非递归

使用栈保存二叉树的最左子节点，然后依次出栈，改变出栈元素的left和right指针。如果出栈元素存在右子节点，则以右子节点为根节点进行出栈入栈操作。

    public TreeNode Convert(TreeNode pRootOfTree) {
            if(pRootOfTree == null) return null;	//树为空
            Stack<TreeNode> stack = new Stack<>();
            TreeNode head  = null;	//保存头节点
            TreeNode pre = null;	//保存上一个节点

            while(!stack.isEmpty() || pRootOfTree != null){	//栈不为空 或 当前节点不为空
                while(pRootOfTree != null){		
                    stack.push(pRootOfTree);	//依次将最左节点入栈
                    pRootOfTree = pRootOfTree.left;
                }
                pRootOfTree = stack.pop();	//出栈
                if(head == null){	//头节点为空
                    head = pRootOfTree;
                    pre = pRootOfTree;
                }else{		
                    pre.right = pRootOfTree;	//连接上一节点与当前节点
                    pRootOfTree.left = pre;	
                    pre = pRootOfTree;		//更新上一节点为当前节点
                }
                pRootOfTree = pRootOfTree.right;	//更新当前节点为右子节点
            }
            return head;
        }