The Involution Principle
Catalan Paths
从 \((0,0)\) 走到 \((n,n)\), 每次只能向上或者向右走,不能穿过直线 \(y=x\) 的方案数。
设从 \((0,0)\) 到 \((n,n)\) 的路径集合为 \(S\), 从 \((1,0)\) 到 \((n+1,n)\) 的路经集合 \(S^+\), 从 \((0,1)\) 到 \((n+1,n)\) 的路经集合 \(S^-\), 显然有 \(|S^+|=\binom{2n}{n},|S^-|=\binom{2n}{n-1}\)。 对于一条路径 \(W\in S^+\cup S^-\),让 \(\phi W\) 表示一条路径,如果 \(W\) 没有穿过 \(y=x\), 那么 \(\phi W=W\),否则 \(\phi W\) 表示 \(W\) 关于 \(W\) 与 \(y=x\) 的第一个交点的对称路径。
显然对于任意一条路径 \(W\in S^-\), 它都会穿过 \(y=x\), 并且 \(\phi W\in S^+\), 所以 \(C_n=\binom{2n}{n}-\binom{2n}{n-1}=\frac{\binom{2n}n}{n+1}\)
Vandermonde Determinant
\(\det\begin{gathered}\begin{pmatrix} x_1^{n-1} & x_2^{n-1} & ... & x_n^{n-1} \\ x_1^{n-2} & x_2^{n-2} & ... & x_n^{n-2} \\ ... \\ x_1 & x_2 & ... & x_n \\ 1 & 1 & ... & 1 \end{pmatrix}\end{gathered}=\prod\limits_{1\le i<j\le n}(x_i-x_j)\)
Proof.
\(\text{The left-hand side}\colon\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)x_{\sigma(1)}^{n-1}x_{\sigma(2)}^{n-2}\cdots x_{\sigma(n)}^0\)
\(\text{The right-hand side}\colon(-1)^mx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\ (\sum\limits_{i=1}^na_i=\binom{n}{2},m=\#\{j\colon x_j\text{ is taken from }x_i-x_j\})\)
考虑建立竞赛图 \(T\), 对于一条边 \(e=(u,v)\) 我们称 \(u\) 是赢家,并定义 \(e\) 的权重:\(w(e)=x_u\text{ with sign }e=\begin{cases}1 & u<v\\-1 & u>v\end{cases}\)
再定义 \(w(T)=\prod\limits_{e\in T}w(e),\text{sign }T=\prod\limits_{e\in T}\text{ sign }e\)
那显然就有 \(\prod\limits_{1\le i<j\le n}=\sum\limits_{T}(\text{sign }T)w(T)\)
从另一个方面也很好解释为啥这两个很容易能看成相等的,因为竞赛图个数和 \(\prod\limits_{1\le i<j\le n}\) 拆开之后的项数都是 \(2^{\binom{n}{2}}\)
于是现在只需要建立竞赛图与行列式的关系。
首先考虑所有无环的竞赛图,显然可以给 \(1,2...n\) 排一个序构成排列 \(\sigma\), 容易观察到 \(w(T_{\sigma})=x_{\sigma(1)}^{n-1}x_{\sigma(2)}^{n-2}\cdots x_{\sigma(n)^0},\text{ sign }T_{\sigma}=(-1)^{\text{inv }\sigma}=\text{sign }\sigma\)
所以有 \(\det=\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)w(T_{\sigma})\)
现在考虑想办法过滤掉有环的竞赛图,让集合 \(S\) 表示所有有环的竞赛图集合, \(S^+=\{T\in S\colon \text{sign }T=1\},S^-=\{T\in S\colon \text{sign }T=-1\}\)
对于一个有环的竞赛图 \(T\),显然会存在一些点对使得其入度相同,我们找出所有点对中最小的点 \(i_0\) 和与 \(i_0\) 入度相同的最小的点 \(j_0\), 那么对于一个点 \(k\not= i_0, j_0\), 不妨设 \(i_0\rightarrow j_0\),那么三元组 \(i_0,j_0,k\) 之间的连边关系只可能有下面四种情况:

显然有 \(\#\text{II}=\#\text I + 1\)
考虑设 \(\phi T\) 表示图 \(T\) 将边 \((i_0,j_0)\) 反向后得到的新图,显然有 \(\text{sign }T=-\text{sign }\phi T,w(T)=w(\phi T)\),且一个在 \(S^+\) 中,一个在 \(S^{-}\) 中,于是这些图的贡献会被抵消掉,故原式得证.
The Pfaffian
称对于集合 \(\{1,2...n\}\) 的任意一个两两划分为在 \(\{1,2...n\}\)上的一个匹配 \(\mu\),写作 \(\mu=i_1j_1,i_2j_2,...,i_{n/2}j_{n/2}\text{ with }i_k<j_k\text{ for all }k\),对于一个斜对称矩阵 \(A\),我们记一个符号 \(a_{\mu}=a_{i_1j_1}a_{i_2j_2}\cdots a_{i_{n/2}j_{n/2}}\)
为了定义 \(\mu\) 的符号,考虑画图列出 \(1,2...;\#\mu\) 表示匹配交叉的数量,并且 \(\text{sign }\mu=(-1)^{\#\mu}\)
对于这个矩阵 \(A\),我们定义 \(pfaffian\text{ Pf}(A)=\sum\limits_{\mu}(\text{sign }\mu)a_{\mu}\)
那么有定理 \(\det A=[\text{Pf}(A)]^2\)
Proof.
首先还是考虑行列式的常见形式 \(\det A=\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)a_{\sigma}\ (a_{\sigma}=a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)})\)
定义 \(S\) 是所有排列中至少包含一个奇环的排列的集合。对于 \(\sigma\in S,\text{let }\sigma=\sigma_1\sigma_2\cdots\sigma_t\) 为其环分解,其中 \(\sigma_1\) 是所有奇环中最小标号所在的奇环,然后定义

显然除了 \(\sigma_1=(k)\) 的情况有 \(a_{\sigma}=-a_{\sigma'},(\text{sign }\sigma)a_{\sigma}=-(\text{sign }\sigma')a_{\sigma'}\), 而对于 \(\sigma_1=(k)\) 的情况,显然有 \(a_{\sigma}=0\)。
于是可以获得结论:\(\det A=\sum\limits_{\sigma\in E}(\text{sign }\sigma)a_{\sigma}\),其中 \(E\in S(n)\) 是所有只包含偶环的排列。
要证明定理,需要找到一个 \((\mu_1,\mu_2)\) 到 \(\sigma\in E\) 的双射关系 \(\phi\) 使得 \((\text{sign }\mu_1)a_{\mu_1}\cdot (\text{sign }\mu_2)a_{\mu_2}=(\text{sign }\sigma)a_{\sigma}\),这里简单举一个例子:
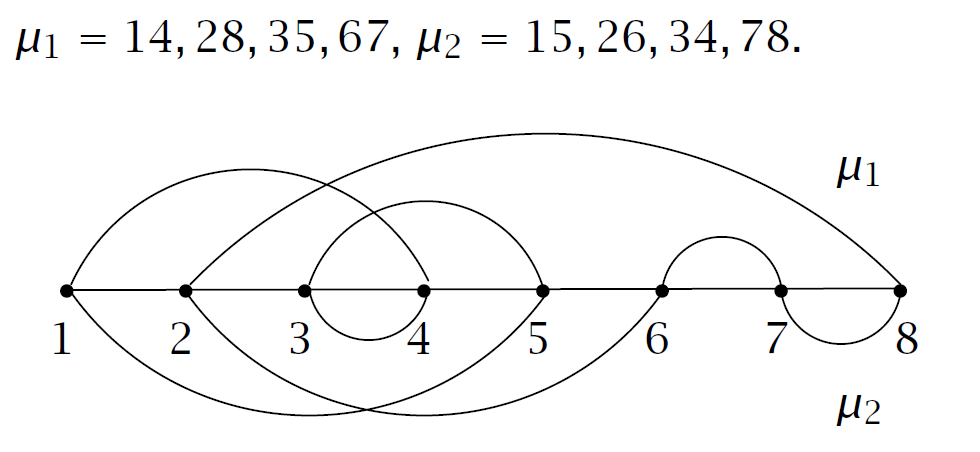
先不考虑符号的问题观察一番。
考虑正向拼凑 \(\sigma\), 考虑如下过程:每次选出未访问过的最小标号点,然后依次沿着 \(\mu1,\mu2\) 中的匹配边走,最后一定会走出若干个偶环。
考虑反向求 \(\mu1,\mu2\) ,考虑如下过程:每次选一个偶环,从上面的最小标号点开始依次把边划分给 \(\mu1,\mu2\)。
现在就只用考虑符号是否能对上。
假设 \(\phi(\mu_1,\mu_2)=(-1)^{e(\sigma)}a_{\sigma},e_(\sigma)=\#\{i\colon i>\sigma(i)\}\)
令 \(\sigma\) 的环分解是 \(\sigma_1\sigma_2\cdots\sigma_t;\) 那么 \(\text{sign }\sigma=(-1)^t\)
所以只需要证明 \(\text{sign }\mu_1\cdot\text{sign }\mu_2=(-1)^{e(\sigma)+t}\) 即 \(\#\mu_1+\#\mu_2-e(\sigma)\equiv t\ (\text{mod 2})\)
容易证明,对于这个环分解,如果我们交换 \(i,i+1\) 的位置,得到的 \(\#\mu_1'+\#\mu_2'-e(\sigma)'\) 和 \(\#\mu_1+\#\mu_2-e(\sigma)\) 奇偶性相同,故可以把 \(\sigma\) 经过多次交换变成
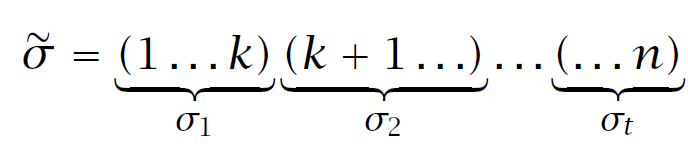
把匹配画出来显然长这样
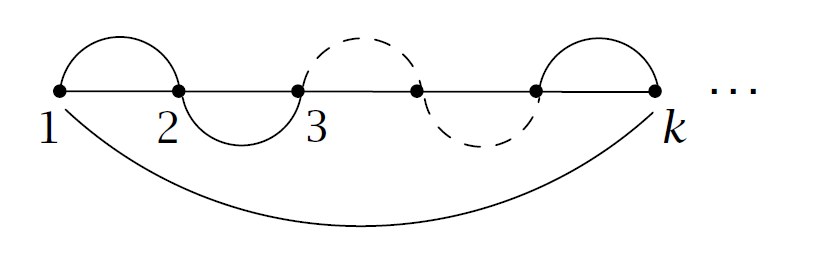
显然对于这个东西, \(\#\mu_1'=\#\mu_2'=0,e(\sigma)'=t\) ,故原定理得证.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号