杂题题解

目录

「SNOI2019」数论

感觉编了个不太大众的做法？

首先假设有如下方程组：

\[\begin{cases} x\equiv a_1\mod P\\ x\equiv a_2\mod Q\\ g=\gcd(P,Q) \end{cases} \]

那么设 \(P'=\frac Pg,Q'=\frac Qg,invP=P'^{-1}\mod Q',invQ=Q'^{-1}\mod P'\)

显然 \(x\equiv Q'invQa_1+P'invPa_2\mod P'Q',a_1\equiv a_2\mod g\)

那么 \(x=((Q'invQa_1+P'invPa_2)\mod P'Q'+kP'Q')g,k\ge0\)

这样枚举 \(a_1,a_2\) 模 \(g\) 的余数 \(r\) 然后分别统计答案即可，整的循环节的方案数是两个集合中模 \(g\) 为 \(r\) 的数个数之积

而对于剩下的不是整的循环节，可以 \(sort\) 之后快速统计

code

「HNOI2019」白兔之舞

感觉是 HNOI2019 里相对简单的题目

\[\begin{aligned} Ans_k=&\sum\limits_{i=0}^{L}[i\mod K==k]C_L^i(W^i)[x][y]\\ =&\sum\limits_{i=0}^L(\frac1K\sum\limits_{j=0}^{K-1}\omega_{K}^{(i-k)^j})C_L^i(W^i)[x][y]\\ =&\frac1K\sum\limits_{j=0}^{K-1}\omega_K^{-jk}\sum\limits_{i=0}^LC_L^i((W\omega_K^j)^i)[x][y]\\ =&\frac1K\sum\limits_{i=0}^{K-1}\omega_K^{-ik}(\omega_K^iW+I)^L[x][y]\\ 设a_i=&(\omega_K^iW+I)^L[x][y]\\ Ans_k=&\frac1K\sum\limits_{i=0}^{K-1}\omega_K^{-ik}a_i\\ -ik=&C_{k-i}^2-C_k^2-C_{i+1}^2\\ Ans_K=&\frac{\omega_K^{C_{k-i}^2}}K\sum\limits_{i=0}^{K-1}a_i\omega_{K}^{-C_{i+1}^2}\omega_{K}^{-C_{k-i}^2}\\ \end{aligned} \]

然后用 mtt 实现循环卷积即可
code

[luogu5591]小猪佩奇学数学

直接推式子：

\[\begin{aligned} Ans=&\sum\limits_{i=0}^nC_n^ip^i\lfloor\frac ik\rfloor\\ =&\sum\limits_{x=0}^{k-1}\sum\limits_{i=0}^n[i\mod k==x]C_n^ip^i\frac{i-x}k\\ =&\frac1k\sum\limits_{x=0}^{k-1}\sum\limits_{i=0}^n(\frac1k\sum\limits_{y=0}^{k-1}\omega_k^{(i-x)y})(i-x)C_n^ip^i\\ =&\frac1{k^2}(\sum\limits_{y=0}^{k-1}(\sum\limits_{i=0}^n\omega_k^{yi}C_n^ip^ii)(\sum\limits_{x=0}^{k-1}\omega_k^{-xy})-\sum\limits_{x=0}^{k-1}x\sum\limits_{y=0}^{k-1}\omega_k^{-xy}\sum\limits_{i=0}^nC_n^ip^i\omega_k^{yi})\\ =&\frac1{k^2}(k\sum\limits_{i=0}^nC_n^ip^ii-\sum\limits_{y=0}^{k-1}(\omega_k^yp+1)^n\sum\limits_{x=0}^{k-1}\omega_k^{-xy}x)\\ \end{aligned} \]

前面可以组合方法变形，后面可以等比数列求和，然后就做完了
code

「2017 山东一轮集训 Day7」逆序对

考虑设 \(f_{i,j}\) 表示 \(1\) 到 \(i\) 的排列逆序对数为 \(j\) 的方案数

那么显然有转移 \(f_{i,j}=f_{i-1,j-i+1}+f_{i-1,j-i+2}+\cdots+f_{i-1,j}\)

写成生成函数的形式： \(f_i(x)=f_{i-1}(x)*(1+x+\cdots+x^{i-1})=f_{i-x}(x)*\frac{1-x^i}{1-x}\)

那么 \(f_n(x)=\frac{\prod\limits_{i=1}^n(1-x^i)}{(1-x)^n}\)

发现可以拆开分子分母，分母的每项系数是组合数，只需考虑分子

\[\begin{aligned} &\prod\limits_{i=1}^n(1-x^i)\\ =&e^{\sum\limits_{i=1}^n\ln(1-x^i)}\\ ln(1-x^i)=&\int(ln(1-x^i))'\text dx\\ =&-\sum\limits_{j\ge1}\frac{x^{ij}}j \end{aligned} \]

这样的话可以调和级数预处理分子取对之后生成函数，写个 mtt 的 exp 即可

code

「XXOI 2018」AK YOI

考虑用点分治统计答案，每次更新整个子树的值，但是由于对于每个儿子管辖的子树统计时需要扣掉儿子子树的贡献，因此用主席树维护长度最值即可

复杂度 \(O(n\log n^2)\)
code

「2017 山东一轮集训 Day1」Sim

首先得会树套树数颜色的做法

大概是对每个位置维护下一个跟当前位置颜色相同的位置的信息，这样可以差分出答案

但是考虑到这题涉及到的区间是动态的，因此我们先按照题目的顺序用 Treap 把历史中所有位置提出来排序，这样就转化成了静态序列的问题

然后用树套树维护就行了

复杂度 \(O(n\log n^2)\)

code

「2017 山东一轮集训 Day2」Pair

题目等价于判断 \(n-m+1\) 次完美匹配，每次加入一个数删除一个数

然后注意到 \(b\) 数组无论是什么顺序都不影响匹配，因此从小到大排序

考虑霍尔定理，发现对于第 \(i\) 个位置至少需要有 \(i\) 条匹配边才能有完美匹配

然后用线段树维护每个位置的匹配边和匹配边下界的差量最小值来判断即可

code

「2017 山东一轮集训 Day1」Sum

过了之后搜题解发现网上好多神仙都写的倍增

实际上考虑 \(dp\) ， \(f_{i,j,k}\) 表示长度为 \(i\) ，模 \(p\) 为 \(j\) ，数字和为 \(j\) 时的方案数

显然有如下转移： \(f_{A,x,a}*f_{B,y,b}\rightarrow f_{A+B,x*10^B+y,a+b}\)

化成矩阵之后相当于每次先把每一行转点值，然后暴力乘一下，然后转回去（如果把 \(p\) 加强得大一点就需要用 \(ntt\) 加速）

那么直接快速幂就行了，每次两个矩阵做一次乘法

code

[WOJ#4845] 小 B 的农场

在一个 \(W*H\) 的网格中有 \(n\) 个障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的周长最大的子矩形。

考试的时候没有分析出好的性质只写了暴力

那么 \(O(n^2)\) 暴力咋做呢？

先暴力枚举矩形上边界，然后动态枚举下边界同时维护左右的边界更新答案即可

现在考虑到最后的答案一定大于 \(\max(W,H)*2\) ，也就是说这个矩形至少跨过了 \(x=\frac W2,y=\frac H2\) 这两条直线中的一条

那么我们两维分别处理一下即可

假设是至少跨过矩形左右的分界线，那么从上到下枚举下边界，用线段树+单调栈维护每个上边界对应左右边界的信息即可
code

「BalticOI 2013」Vim

考虑到如果要删掉一个 \(e\) ，那么一定是先到达这个 \(e\) 前面一个点，然后按 \(hx\) 删掉 \(e\) ，那么不妨删掉所有 \(e\) 并且把它前面一个字符标记为必经点，并且每个 \(e\) 对答案有 \(2\) 的贡献
根据题目叙述，现在有两个操作：

  1. 左移
  2. 向右跳到某个字符第一次出现的地方

那么对于最优决策一定满足对于任意的 \((i,i+1)\) 都最多从 \((i+1)\) 向 \(i\) 左移了一次

设序列长度为 \(n\) ，那么我们手动添加一个 \(s_{n+1}=*\) 且最后一定要跳到 \(n+1\) 这个位置，这样的话对于每个被经过的 \((i,i+1)\) 只有如下两种经过情况：
情况1
情况2
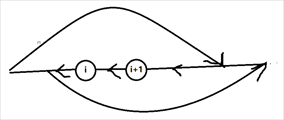
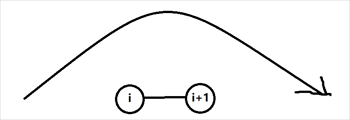
于是就可以 \(dp\) 了
\(f_{i,j,k}\) 表示当前处理到 \((i,i+1)\) ， \((i,i+1)\) 被横跨了两次，两条线中更靠左的左端点的值为 \(j\) ，更靠右的右端点的值为 \(k\) 时的最优值
\(g_{i,j}\) 表示当前处理到 \((i,i+1)\) ， \((i,i+1)\) 被横跨了一次，横跨的线的右端点的值为 \(j\) 时的最优值
然后讨论 \((i-1,i)\) 被几条线跨过，以及 \((i-1,i)\) 和 \((i,i+1)\) 共用的线来转移即可
复杂度为 \(O(nk^2)\)
code

「2017 山东一轮集训 Day3」第三题

直接写了个 mtt + 多点求值就过了...
code
过了之后意识到问题应该没有这么简单，下面讨论一波正经的做法：
为了方便先特判掉 \(c=0\) 的情况，以下叙述时默认 \(c\not=0\)
首先研究数据范围发现有 \(b=0\) 的部分分，不难想到需要按照 \(b\) 的大小进行讨论
当 \(b=0\) 时：

\[\begin{aligned} f(x_k)=&\sum\limits_{i=0}^na_i(dc^{2k}+e)^i\\ =&\sum\limits_{i=0}^na_i\sum\limits_{j=0}^iC_i^jd^jc^{2kj}e^{i-j}\\ =&\sum\limits_{i=0}^n\frac{d^ic^{2ki}}{i!}\sum\limits_{j=i}^{n}a_jj!*\frac{e^{j-i}}{j!}\\ 令g_i=&\sum\limits_{j=i}^{n}a_jj!*\frac{e^{j-i}}{j!}\\ f(x_k)=&c^{k^2}\sum\limits_{i=0}^n\frac{d^ig_ic^{i^2}}{i!}*\frac1{c^{(k-i)^2}} \end{aligned} \]

两次 mtt 分别处理 \(g,x\) 即可
当 \(b\not=0\) 时：

\[\begin{aligned} bc^4+dc^2+e=&b(c^2+\frac d{2b})^2+e-\frac{d^2}{4b}\\ 令d'=&\frac d{2b},e'=e-\frac{d^2}{4b}\\ f(x_k)=&\sum\limits_{i=0}^na_i(b(c^{2k}+d')^2+e')^i\\ =&\sum\limits_{i=0}^na_i\sum\limits_{j=0}^iC_i^jb^j(c^{2k}+d')^{2j}e'^{i-j}\\ =&\sum\limits_{i=0}^n\frac{b^i(c^{2k}+d)^{2i}}{i!}\sum\limits_{j=i}^na_jj!\frac{e'^{j-i}}{(j-i)!}\\ 令g_i=&\sum\limits_{j=i}^na_jj!\frac{e'^{j-i}}{(j-i)!}\\ f(x_k)=&\sum\limits_{i=0}^n\frac{b^ig_i(c^{2k}+d)^{2i}}{i!}\\ =&\sum\limits_{i=0}^n\frac{b^ig_i}{i!}\sum\limits_{j=0}^{2i}C_{2i}^jc^{2kj}d^{2i-j}\\ =&\sum\limits_{i=0}^{2n}\frac{c^{2ki}}{i!}\sum\limits_{j=\lfloor\frac i2\rfloor}^n\frac{b^jg_j(2j)!c^{2kj}}{j!}*\frac{d^{2j-i}}{(2j-i)!}\\ 令h_i=&\sum\limits_{j=\lfloor\frac i2\rfloor}^n\frac{b^jg_j(2j)!c^{2kj}}{j!}*\frac{d^{2j-i}}{(2j-i)!}\\ f(x_k)=&c^{k^2}\sum\limits_{i=0}^{2n}\frac{h_ic^{i^2}}{i!}\frac1{c^{(k-i)^2}} \end{aligned} \]

三次卷积分别处理 \(g,h,x\) 即可
代码咕了

[CF906E]Reverses

考虑构造串 \(s_1t_1s_2t_2...s_nt_n\)
然后找最小回文分解即可
注意到这题可以不换区间，那么当 \(s'_i==s'_{i-1}\) 的时候需要用 \(f_{i-2}\) 来更新 \(f_i\)
最后倒序输出方案即可
code

[luogu5825]排列计数

设 \(f_{i,j}\) 表示 \(i\) 个位置， \(j\) 个空隙满足 \(a_i<a_{i+1}\) 的方案数
考虑比较明显的递推式 \(f_{i,j}=f_{i-1,j}*(j+1)+f_{i-1,j-1}*(i-j)\) 并不好转化，于是换个思路
考虑组合意义，假设钦定 \(X\) 个空隙一定为 \(a_i<a_{i+1}\) 并合并 \(i,i+1\) 所在的集合，那么最后的方案数就是 \(n-1-X\) 个非空集合凑成序列的方案数，即 \((e^x-1)^{n-X-1}[x^n]\) ，展开之后就是常规做 ntt 卷积，设得到的序列的 \(OGF\) 为 \(F\) ，那么显然 \(F,Ans\) 这两个生成函数可以二项式反演
于是两次卷积即可
code

[luogu5655]基础数论函数练习题

首先考虑对于一个数列 \(a\) 怎么求它们的 \(\text{lcm}\) ，考虑对每个位置维护一个 \(b_i\) 使得 \(b_i|a_i\) 且 \(\prod b_i=\text{lcm}(a_1,a_2,...,a_n)\)
那么从左到右依次插入每个数，这样复杂度可以做到 \(n\log V+n^2\) ，总复杂度是 \(O(Tqn(n+\log V))\)
考虑分治优化，对于每一层维护从分治中心向左/右的后缀/前缀的 \(b\) 数组，显然可以暴力插入 \(b_mid\rightarrow b_l\) 做到 \(O(Tn^2\log V+q)\) 的复杂度了
考虑继续优化掉后面的 \(\log\) ，设 \(c_i=\text{lcm}_{j=mid+1}^ib_j\) ，发现在插入一个 \(b_p\) 之后原本的 \(b_i,(i>mid)\) 变成 \(\frac{\text{lcm}(c_i,b_p)}{\text{lcm}(c_{i-1},b_p)}=\frac{b_i}{\gcd(c_i,b_p)/\gcd(c_{i-1},b_p)}\) ，而 \(\gcd(c_{i-1},b_p)=\gcd(c_i,c_{i-1},b_p)\) ，因此这个 \(\log V\) 被摊在了 \(n\) 次操作中，复杂度变成了 \(O(Tn(n+\log V)+q)\) ，可以通过该题
code

[AGC034F] RNG and XOR

设 \(x_i\) 表示初始值为 \(i\) 时，第一次异或结果为 \(0\) 的期望时间，那么有如下等式：

\[\begin{aligned} x_i=&1+\sum\limits_{j}x_jp_{i\oplus j}(i>0)\\ x_0=&0 \end{aligned} \]

那么写成异或卷积的形式就是 \((x_0,x_1,...)\oplus(p_0,p_1,...)=(?,x_1-1,x_2-1,...)\)
考虑 ? 处的值，由于 \((\sum\limits_{i\ge0}x_i)*(\sum\limits_{i\ge0}p_i)=1=(?+\sum\limits_{i>0}x_i-1)\)，所以 \(?=x_0+2^n-1\)
然而两边都含有 \(x_i\) 不好转化，考虑用 \(p_0-1\) 替换 \(p_0\) ，这样结果的每个位置 \(i\) 都会减去 \(x_i\) ，即：\((x_0,x_1,...)\oplus(p_0-1,p_1,...)=(2^n-1,-1,-1,...)\)
于是转 fwt 做个异或卷积意义下的除法再 ifwt 回去即可！
上一行的做法显然有问题
考虑到 \((p_0-1,p_1,...),(2^n-1,-1,-1,...)\) 这两个序列在 fwt 之后第 0 个位置都是 0 ，除法没有意义，而其余位置都得到了正确的点值，因此我们设这个位置原本的点值应该是 X ，发现 ifwt 的时候会给每个位置都减少一个 X 的贡献，那么 ifwt 后第 0 个位置的数就是 -X ，手动给所有位置都加上 X 即可
code

[51nod2583] 数论只会 Gcd

首先如果 \(x\le y\) 那么 \(\gcd(x,y)\) 调用次数显然为 \(0\)
然后考虑 \(x>y\) 的情况，显然在若干次取模操作之前一定是 \(\gcd(ax+by,cx+dy)\) 的形式，发现每次可以进行两种变化：

  1. \((ax+by,cx+dy)\rightarrow((a+c)x+(b+d)y,cx+dy)\)
  2. \((ax+by,cx+dy)\rightarrow(ax+by,(a+c)x+(b+d)y)\)

然后发现这十分类似 SBT 的生成方式，且每一对相邻的节点对应两种执行，因此对于每个真分数 \(\frac ab\) 对应了 4 次执行（它有两个相邻的祖先），不过由于第一次一定是变成 \((x,x+y)\) ，因此 1 只能对应两次执行
这样问题就变成了求这个玩意儿: \(\sum\limits_{1\le i,j\le m}[i\ge j][\gcd(i,j)==1](ix+jy\le m)\)
直接杜教筛+类欧几里得即可
code

[WOJ#4854] A

给出两个序列 L,R ，一个数 D ，和一个集合 T ，你需要计数有多少个长度为 N 的正整数序列 \(A_1,...,A_n\) ，满足如下条件：

  1. 对于任意 \(\forall 1\le i\le N,s.t.L_i\le A_i \le R_i\)
  2. 记 \(S=\sum\limits_{i=1}^NA_i\) ，把 S 在 D 进制下的表示写出来，去掉所有前导0，满足每一个数位都在集合 T 中出现过。
    答案对 \(10^9+7\) 取模

考虑假如求出一个合法的 D 进制数 V ，答案可以简单的 \(2^n\) 枚举每个位置是否取到上界容斥算，对于每种方案，设其和为 \(S\) ，那么方案数为 \(C_{V-S-1}^{n-1}\)，不妨令 S 加 1 ，这样对于每个容斥出来的 S ，我们要求的是 \(\sum\limits_{V合法}C_{V-S}^{n-1}=\sum\limits_{V合法}\sum\limits_{x=0}^{n-1}C_{V}^{x}C_{-S}^{n-x-1}\)
这下只用数位 dp 处理前面的即可，转移也需用上范德蒙德恒等式转移
code

[SnarkNews New Year Contests-2019] Gnutella Chessmaster

给出一个 \(n*n\) 的棋盘，对于 \(i=1,...,2*n-1\) 求有多少种放 \(i\) 个象在棋盘上的方案使得象两两不攻击

如果是放車的话就是 rook 多项式板题实际上这题也是，考虑到象是斜着走的，那么我们把棋盘转动 45 度，这样就等价于两个互不干扰的棋盘来放車，那么分别用 rook 多项式搞搞再卷积一下即可
以防博主忘记这里记一下 rook 多项式的结论，假设有 n 行，每行格子数从小到大排序后分别是 \(a_1,a_2,...,a_n\) ，设 \(f_i\) 表示放 \(i\) 个車的方案数，那么 \(\sum\limits_{i=0}^nf_ix^{\underline{n-i}}=\prod\limits_{i=1}^n(x+a_i-i+1)\)
注意这个地方的 fdt 不用写多点求值，因为两个 rook 多项式分别是 \(x^{\lfloor\frac n2\rfloor}(x+1)x^{\lceil\frac n2\rceil},(x+2)^{\lfloor\frac n2\rfloor}(x+1)^{\lfloor\frac (n-1)2\rfloor}\) ，因此直接快速幂求 \(n\) 次点值即可
code

[51nod1961] Power Sum

设 \(F(x)=\sum\limits_{i=0}^{+\infty}p_ix^i\)
先推推式子容易得到 \(F(x)=n-x(\ln\prod\limits_{i=1}^n1-a_ix)'\)
不会的可以先做做这道题
于是移项可以得到 \(\prod\limits_{i=1}^n1-a_ix=e^{\int\frac{n-F(x)}x\text dx}=G(x)\)
于是只用求 G(x) 的所有零点，这个容易用几次 dft 做到 \(O(mod\log mod)\) ，注意要特判 G(0)
code

[Dwango Programming Contest 6th] E. Span Covering

由于博主比较菜于是只编了一个比较傻的 \(O(n^2X^2)\) 的 dp ，貌似容斥能做到 \(O((X+n)X^2)\) 然而没想到...
考虑把所有线段按长度从大到小排序排序，然后一根一根放上去，对于每个点我们定义它的编号是第一次覆盖它的线段编号
然后就可以 dp 当前所有线段组成的连续段了，考虑每次将当前线段插入到现有的连续段中，要么插到端头/端尾，要么插到两个相邻且不相交的线段中
于是我们设 \(f_{i,j,k}\) 表示处理完前 i 条线段，现在有 j 个空隙可以插入线段（不包括端头/端尾），且连续段总长度为 k 的方案数，然后转移即可
code

posted @ 2020-02-06 23:00  soroboruo  阅读(609)  评论(0)    收藏  举报