最大最小堆排序--Java实现
最小堆排序:
自底向上进行大顶堆的调整。
//用于将堆调整成大顶堆,init是为了判断当前调整是否为初始化调整。
static void smallHeapAdjust(Integer[] list,int length,boolean init) throws Exception {
int index = (length - 1) / 2;
int maxIndex = 0;
//当最后一个非叶子节点为堆的根节点时,返回。
if(index <= 0){
return;
}
//用于初始化时调整且判断是否为完全二叉树
if(list[index] != null && init){
if(list[(index+1)*2-1] != null){
if(list[(index+1)*2-1] > list[index]){
int temp = list[index];
list[index] = list[(index+1)*2-1];
list[(index+1)*2-1] = temp;
}
}
else{
if(list[(index+1)*2] != null){
throw new Exception("非完全二叉树");
}
}
}
maxIndex = list[index*2-1] > list[index*2] ? index*2-1 : index*2;
if(list[maxIndex] > list[index-1]){
int temp = list[maxIndex];
list[maxIndex] = list[index-1];
list[index-1] = temp;
}
smallHeapAdjust(list,length - 2,init);
}
判断当前大顶堆是否符合规则
//用于判断当前堆是否为大顶堆,init用于初始化判断
public static boolean checkSmallHeap(Integer[] list,int length,boolean init) throws Exception {
for(int i = 1;i <= (length - 1) / 2;i++){
if(list[i-1] < list[(i * 2 - 1)] || list[i-1] < list[i*2]){
return false;
}
if(i == (length - 1) / 2){
if(list[i+1] != null && init){
if(list[(i+1)*2-1] != null){
if(list[(i+1)*2-1] > list[i+1]){
return false;
}
}
else{
if(list[(i+1)*2] != null){
throw new Exception("非完全二叉树");
}
}
}
}
}
return true;
}
先对无序堆进行初始化,再将堆顶元素与无序区的最后一个元素进行交换,再重新调整。
//最小堆排序
public static void smallestHeapSort(Integer[] list) throws Exception {
//初始化大顶堆
while (!checkSmallHeap(list,list.length,true)){
smallHeapAdjust(list,list.length,true);
}
//将调整完成的大顶堆的根节点与无序区的最后一个节点进行交换,交换完成之后,最后一个节点就被归为有序区
for(int i = list.length;i >= 1;i--){
int temp = list[0];
list[0] = list[i-1];
list[i-1] = temp;
//每次交换完之后需要对无序区的堆进行调整
while (!checkSmallHeap(list,i-1,false)){
smallHeapAdjust(list,i-1,false);
}
}
}
首先根据该数组元素构建一个完全二叉树,得到
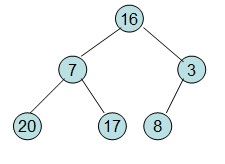
然后需要构造初始堆,则从最后一个非叶节点开始调整,调整过程如下:
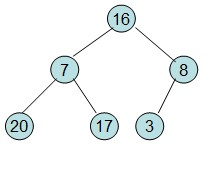
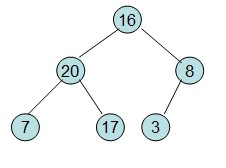
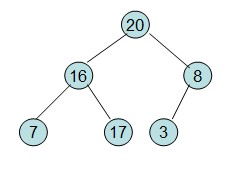
20和16交换后导致16不满足堆的性质,因此需重新调整
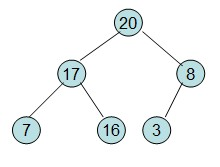 这样就得到了初始堆。
这样就得到了初始堆。
即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。
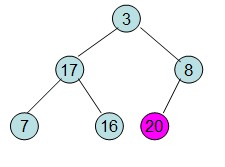 此时3位于堆顶不满堆的性质,则需调整继续调整
此时3位于堆顶不满堆的性质,则需调整继续调整
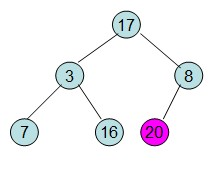
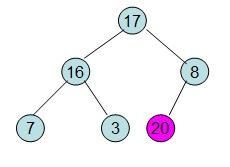
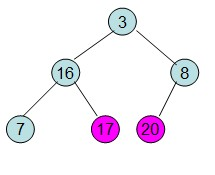
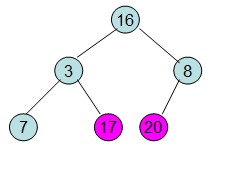
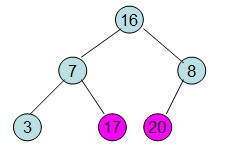
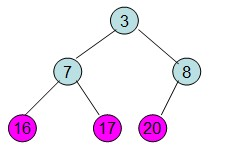
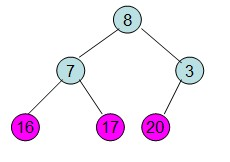
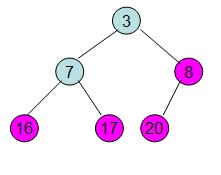
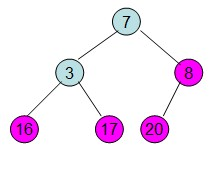
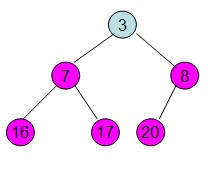
这样整个区间便已经有序了。
最大堆排序:
将调整判断大顶堆改为调整判断小顶堆




 浙公网安备 33010602011771号
浙公网安备 33010602011771号