【搬运】【射电天文工具第4版中文】【第09章】连续辐射发射机制 粗读

### 9.1 射电源分类 20220705Tue
按辐射机制：热与非热（由同步/磁轫致主导）。
按空间区划：河内源与河外源。
@ 河外源中非热源是主要的，因为一般热源比非热源暗弱而更难观测。
下图是第6版英文图10.1，红线部分是典型的热辐射（宁静太阳，月亮，低频HII区）。

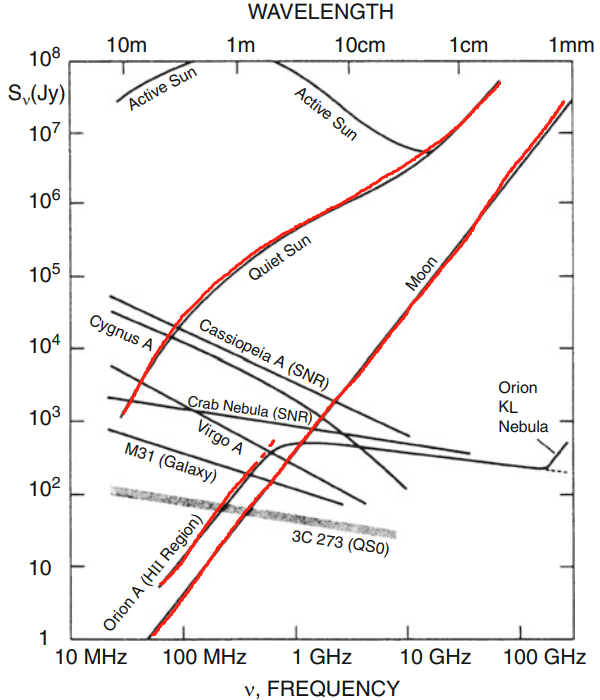
按辐射物体：(a)原子/分子热谱线发射，(b)固体天体热发射，(c)被加速的自由电子。
@ 自由电子可以交换任意大小的能量，没有确定的能量跳跃=没有吸收/发射线。
@ 除非特别指定，否则以下讨论仅限于电子动能相对变化不大于\(\Delta E/E\approx10^{-5}\)的情况。

ovo

### 9.1.1 天体黑体辐射 20220705Tue
光学厚天体（行星等固体天体），光深\(\rightarrow\infty\)，射电测量约一个波长处的温度（盘/表面温度）。
@ 根据辐射转移方程，此时比强度\(I_\nu\)=黑体谱亮度\(B_\nu(T)\)。
分子云尘埃，准确公式，忽略微波背景辐射，尘埃光深\(\tau_\mathrm{dust}\)和氢气柱密度\(N_\mathrm{H_2}\)的关联。尘埃辐射的偏振性质。
@ 温度10~30K的冷尘埃或冷星际介质占据银河系亮质量的大部分。

ovo

### 9.2 单电子加速辐射 20220705Tue
运动电荷辐射的般理论，必须依靠合适电磁势（Lienard-Wiechert势），结果适用于所有的能量范围（热的+相对论的）。
假定观测运动电荷的参考系运动速度小于光速，出现只有依赖于加速度的辐射场分量\(E_\mathrm{\theta}\)，等同于赫兹偶极子的远场辐射。
坡印廷流量（单位面积，单位立体角在方向\((\theta,\phi)\)的功率）的球面积分得到电荷被加速的辐射总功率\(P(t)\propto e^2\dot{v}^2(t)\)。
@ 若\(E\)和\(\dot{v}(t)\)只在很短时间间隔内不为零，那可以对E的脉冲进行傅里叶分析得到E的频率依赖？

ovo

### 9.3 单电子碰撞的轫致辐射频率分布 20220705Tue
ff辐射（电子-离子），p是最近点的距离，v是最近点的速度。
电子e在离子Ze电场运动时辐射的总能量，只适合于直线近似有效（p很大）的低能碰撞。
对感生电场函数\(E(t)\)取傅里叶变换，用频率\(\omega\)的谐波叠加形成的波包来代表这个脉冲。
最后得到轫致辐射能谱密度极限频率\(\omega_\mathrm{g}\propto v/p\)，频率低于\(\omega_\mathrm{g}\)可认为谱线平坦。

ovo

### 9.4 电离气体云辐射 20220706Wed
单次i-e辐射的所有特征，依赖于碰撞参数p和v。而在电离气体云中，这些参数具有很宽的分布，合适的平均才是总辐射。
@ 每个碰撞的辐射将被随机偏振化，于是一个偏振分量的辐射只代表总功率谱的一半。
对相对能量变化小的碰撞，电子速度在碰撞中改变很小，可以用麦克斯韦分布律去近似。
电离气体云热发射系数，\(\varepsilon_\nu\propto(Ze)^2e^4\frac{N_\mathrm{e}N_\mathrm{i}}{m_\mathrm{e}^2}\sqrt{\frac{m_\mathrm{e}}{T}}\ln\frac{p_2}{p_1}\)。
@ 需要对极限值\(p_1=p_\mathrm{min}\)，\(p_2=p_\mathrm{max}\)进行合理估计，否则会对数发散。
若发射系数已知，根据基尔霍夫定律\(\kappa_\nu=\frac{\varepsilon_\nu}{B_\nu(T)}\)计算吸收系数，\(\kappa_\nu\propto\frac{(Ze)^2e^4N_\mathrm{e}N_\mathrm{i}}{\nu^2\sqrt{(m_\mathrm{e}T)^3}}\ln\frac{p_2}{p_1}\)。
若等离子体宏观中性，化学组分\(N_\mathrm{H}:N_\mathrm{He}:N_\mathrm{other}\approx10:1:10^{-3}\)，则\(N_\mathrm{i}=N_\mathrm{e}\)是可取的高精度近似。
若星云视向有效温度\(T_\mathrm{e}\)不变，可以使用光学厚情况下的吸收系数、结合辐射量度(Emission Measure, EM)确定光深，\(\tau_\nu-\int^s_0\kappa_\nu ds\)，最终得到亮度分布转折频率。
@ 转折前，亮温度=色温度；转折后，亮温度<色温度，比例对数线性下降。
@ 转折前，发射强度对数线性增加；转折后，发射强度对数基本稳定。

ovo

### 9.6 回顾洛伦兹变换 20220706Wed
假设两个坐标系的相对速度\(v\)(常数)只沿x向，定义\(\beta=v/c\)，\(\gamma^{-2}=1-\beta^2\)。
坐标变换：\(x=\gamma(x'+vt')\)，\(y=y'\)，\(z=z'\)，\(t=\gamma(t'+\beta x'/c)\)。
定义速度，\(u_x=\frac{dx}{dt'}\frac{dt'}{dt}=\gamma(u'_x+v)\cdot (\gamma\sigma_x)^{-1}=\frac{u'_x+v}{\sigma_x}\)，其中\(\sigma_x=1+\beta u'_x/c\)。
@ \(\Delta t=\gamma\Delta t'\)，\(\frac{dt}{dt'}=\gamma\sigma_x\)，为什么钟慢效应是前者？是因为后者包括了坐标变动（\(\sigma_x\)）吗？
@ 此钟慢效应仅考虑了相对论效应，若两参考系有相对运动（非相对论），则右边还需要乘以一个独立的多普勒因子\(\frac{c+v_r}{c}\)。
速度变换：\(u_x=\frac{u'_x+v}{\sigma_x}\)，\(u_y=\frac{u'_y}{\gamma\sigma_x}\)，\(u_z=\frac{u'_z}{\gamma\sigma_x}\)。
@ 平行与参考系间相对速度的分量\(u_{||}=\frac{u'_{||}+v}{\sigma_{||}}\)，垂直的分量\(u_\perp=\frac{u'_\perp}{\gamma\sigma_{||}}\)。
定义加速度，\(\frac{d\sigma_x}{dt'}=\beta a'_x/c\)，\(\frac{du_x}{dt'}=\frac{\sigma_xa'_x-\beta a'_x/c(u'_x+v)}{\sigma^2_x}=\frac{a'_x}{\gamma^2\sigma^2_x}\)，\(a_x=\frac{a'_x}{\gamma^3\sigma^3}\)；\(\frac{du_y}{dt'}=\gamma\frac{a'_y\sigma_x-\beta u'_ya'_x/c}{\gamma^2\sigma^2}\)，\(a_y=\frac{a'_y\sigma_x-\beta u'_ya'_x/c}{\gamma^2\sigma^3}\)；\(a_z\)形式同\(a_y\)。
@ 平行与参考系间相对速度的分量，垂直的分量\(u_\perp=\frac{u'_\perp}{\gamma\sigma_{||}}\)。
速度和加速度分量都不是四元矢量的分量，所以坐标变换形式并不简洁。

ovo

### 9.7 单电子的同步辐射 20220706Wed
匀强磁场B中以速度v运动的荷子e，服从相对论的爱因斯坦-普朗克方程：\(\frac{d}{dt}(\gamma m\vec{v})=e(\vec{v}\times\vec{B})\)。
若此时无电场E，则由能量守恒知，\(\frac{d}{dt}(\gamma mc^2)=0\)，暗示着\(\gamma\)是常数，\(|\vec{v}|是常数\)。平行磁场分量的速度为常数，\(\frac{d\vec{v}_{||}}{dt}=0\)；垂直磁场分量速度按以上爱-普方程所示，在垂直于磁场B的平面内做圆周运动，且也是常数（知二定一）。螺旋线的螺旋角，\(tan\alpha=\frac{|\vec{v}_\perp|}{|\vec{v}_{||}|}\)。
@ 圆周运动圆频率，\(\omega_\mathrm{B}=\frac{eB}{\gamma m}\)，回旋频率\(\omega_\mathrm{G}=\gamma\omega_\mathrm{B}\)，这两个频率有何区别？一个随动系G？一个观测系B？似乎也不是啊…
@ 加速是在垂直磁场B的径向，\(a_\perp=\omega_Bv_\perp\)。
【9.7.1 辐射总功率】
简单起见，假设平行方向速度分量=0（加速度也=0），在某个无穷小时间内的某个惯性系K'中考察电子（使K'中电子可以看作静止），它此时的辐射功率由拉莫公式给出，\(P'=\frac{2e^2}{3c^3}a'^2_\perp\)。
把\(P'\)转换到K系中，能量是四矢（3动量1能量）的一个分量，有变换\(W=\gamma W'\)，对位置不变的时间间隔也有\(dt=\gamma dt'\)，所以辐射功率\(P'=\frac{dW'}{dt'}=\frac{dW}{dt}=P\)，\(P=P'=\frac{2e^2}{3c^3}a'^2_\perp=\frac{2e^2}{3c^3}a^2_\perp\gamma^4\)，引入电子总能量\(\epsilon\)：\(\gamma=\frac{\epsilon}{mc^2}\)，总之最后得到P与散射截面\(\sigma_T\)、球面均磁场平方\(u_B\)的关系。
【9.7.2 辐射角分布】
\(\theta\)是下俯仰角，\(\theta=0\)是正z向，即某个垂直于磁场B的方向。
随动系K'中，\(\frac{dP'}{d\Omega}\propto(1-\sin^2\theta\cos^2\phi)\)。
静止系K中，\(\frac{dP}{d\Omega}\propto\frac{1}{(1-\beta\cos\theta)^2}(1-\frac{\sin^2\theta\cos^2\phi}{\gamma^2(1-\beta\cos\theta)^2})\)。
平行磁场B方向的束流半角，\(\tan\xi=\frac{u_\perp}{u_{||}}=\frac{c}{\gamma v}\)。
【9.7.3 辐射频率】
与观测者看到的电磁场变化形式有关；强束流效应是高频辐射的原因；只有观测者在束流角内时才可能观测到电子辐射。

### 9.8 同步辐射光谱和偏振 20220706Wed
若电子以相对磁场的常数速度分量（平行和垂直）运动，那么发出的辐射时在电子瞬时运动方向的小锥体内强烈定向的。
该瞬时辐射一般是椭圆偏振的，但由于偏振椭圆位置角随电子旋转，所以时间平均下来偏振是线性的。在平行轨道上单能量电子群发出的辐射也如此。

### 9.9 电子群的同步辐射能谱分布 20220706Wed
研究相对论电子的体发射率\(\varepsilon\)。
同步辐射的谱形状非常独立于辐射区域的磁场强度和几何形状，偏振的状态却与这些量紧密相关。
均匀磁场会产生高度线偏振，完全随机磁场则会消偏振（低偏振）。

### 9.10 同步辐射的能量要求 20220706Wed
源总内能只有在辐射机制已知时才能较好估算。
非热源在射电段一般看不到热辐射，所以射电数据不能很好确定内能。
射电段的非热源能量输出主要是同步辐射形式，此时能量以两种方式存在，相对论粒子动能\(W_p\)和磁场储存的能量\(W_m\)，可以估算他们与观测流量密度\(S_\nu\)的关系。

### 9.11 非热源低能截断的其它说明机制 20220706Wed
（一）在致密高强射电源的低频段，在光学厚时，同步辐射场中自发发射将不可忽略，它的谱指数是-2.5（非热），不同于瑞利-金斯的n=-2（热）。
（二）若射电源星际介质是等离子体，且辐射场频率接近等离子体频率，则高于当地回旋频率所需的相对论束流相应失效，同步辐射在这个频率一下被抑制。
（三）前景热等离子体在低频吸收同步辐射。

### 9.12 逆康普顿散射 20220706Wed
SZ效应：微波背景光子与前景热星系团高能电子相互作用，长波光子移动到短波。
用逆康普顿效应估计高亮度非热源的能量损失。