莫比乌斯反演详解
莫比乌斯反演
积性函数
联考D2T3用到了\(\mu*id=\phi\)
然后还有\(\phi*1=id\)，\(\mu*1=\epsilon\)
证明：
\(n=\prod_{k=1}^{m} p_{k}^{\alpha_{k}}\) ， \(d=\prod_{k=1}^{m} p_{k}^{\beta_{k}}\)，由积性函数的性质，我们把不同质因数的分开算，再带入\(\varphi(N)=N*(1-\frac 1 p)\)即可得到
莫比乌斯函数
\(\mu(n)=1,n=1\)
\(\mu (n)=(-1)^m, n=\prod^m_{i=1}p_i^{k_i},\forall k_i = 1\)
\(\mu (n)=0 ,otherwise\)
性质
- 积性函数
- \(\sum _{i|n} \mu(i)=\epsilon (\epsilon = [n=1])\)
筛法
inline void init(){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!np[i]) pri[++top]=i;
for(int j=1;j<=top&&i*pri[j]<n;j++){
int now=i*pri[j];
np[now]=1;
if(i%pri[j]) mu[now]=-mu[i];
else{
mu[now]=0;break; //出现平方因子
}
}
}
}
狄利克雷卷积
\((f∗g)(n)=∑_{d|n}f(d)∗g(\frac{n}{d})\)
数论函数与狄利克雷卷积形成群，满足结合律，封闭性，单位元，逆元，同时还满足交换律
其中单位元为\(ϵ\)，\(ϵ(n)=[n=1]\)
比较常用的积性数论函数备用
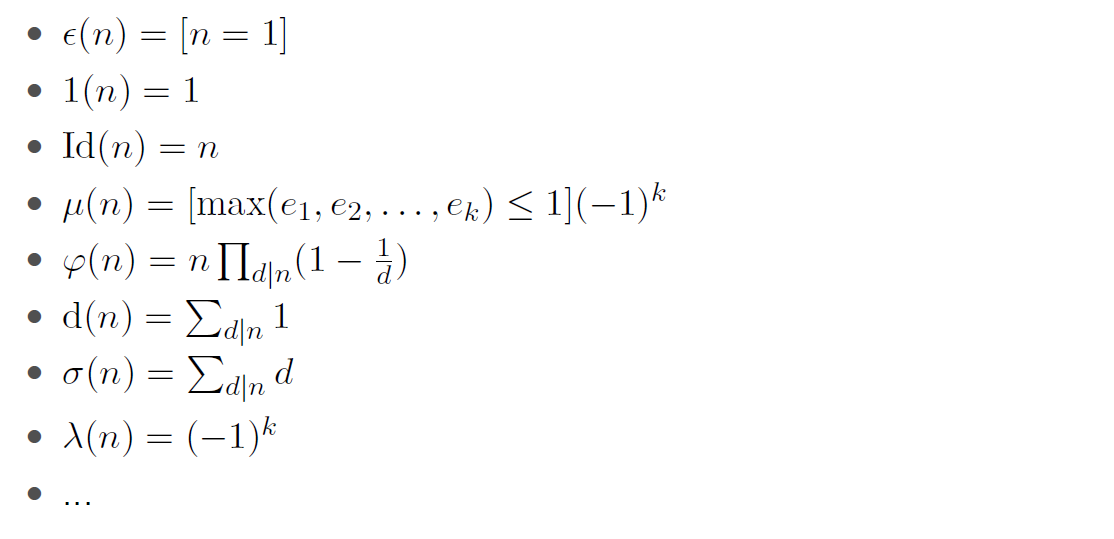
反演
有\(f(n)=\sum_{i|n}g(i)\)
结论：\(g(n)=\sum_{d|n}f(\frac{n}{d})*{\mu(d)}=\sum_{d|n}f(d)\mu(\frac{n}{d})\)
证明
展开f：
提\(\mu\)到前面
换\(\sum\)，注意取值范围
考虑后面\(\sum_{d|\frac{n}{i}}\mu(d)\)
- \(i=n,d=1\) ,此时\(\mu(d)=\mu(1)=1\)，\(g(i)*\sum_{d|\frac{n}{i}}\mu(d)=g(n)\)
- \(i<n,\frac{n}{i}!=1\),此时\(\sum_{d|\frac{n}{i}}\mu(d)=\epsilon(\frac{n}{i})=0\)，乘上 \(g(i)\) 还是 \(0\)
于是两种情况相加就是 \(g(n)\)，原等式成立
用狄利克雷卷积写起来就是\(f=g*1 , g=f*\mu\)
第二种形式
应用
二维gcd数数
对于给定的整数\(a,b\)和\(d\)，有多少正整数对 \(x,y\)，满足 \(x\leq n\)，\(y\leq m\)，并且 \(gcd(x,y)=d\)
要求的数：
转换一下：
法一
利用莫比乌斯函数的性质：
考虑枚举\(g\)，设\(N = \frac{n}{d},M = \frac{m}{d}\)
归类得：
然后后面那个东西的共同取值一种只有\(\sqrt{n}+\sqrt{m}\)种，数论分块求得
法二
还是令
\(f(k)\)为答案，\(g(k)\)明显等于\(\lfloor\frac{n}{k}\rfloor\lfloor\frac{m}{k}\rfloor\)
根据定义，
反演得
套用\(g\),令设\(N = \frac{n}{d},M = \frac{m}{d}\)
然后数论分块
数论分块的tips
对于有两个整除的，我们知道复杂度是\(\sqrt{n}+\sqrt m\)
单个数论分块的实现方法：
假设当前区间开头是\(i\)，并且下一个区间是\(j+1\)
有
两个数的同理，取min就好了
代码：
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
...
}
题解代码：
#include<iostream>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstdio>
#define ll long long
using namespace std;
const int N = 50021;
inline int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
int np[N],pri[N],top,mu[N],tomu[N];
void init(){
mu[1]=1;
for(int i=2;i<N;i++){
if(!np[i]){
pri[++top]=i;
mu[i]=-1;
}
for(int j=1;j<=top&&i*pri[j]<N;j++){
int now=i*pri[j];np[now]=1;
if(i%pri[j]==0){
mu[now]=0;break;
}else{
mu[now]=mu[i]*-1;
}
}
}
for(int i=1;i<N;i++){
tomu[i]=tomu[i-1]+mu[i];
}
}
int T;
int main(){
init();
T=read();
while(T--){
int a=read(),b=read(),d=read();
int n=a/d,m=b/d;
if(n<m) swap(n,m);
int ans=0;
for(int l=1,r;l<=n;l=r+1){
if(n/l==0||m/l==0){
r=n;
}else r=min((n/(n/l)),(m/(m/l)));
ans+=(n/l)*(m/l)*(tomu[r]-tomu[l-1]);
}
printf("%d\n",ans);
}
return 0;
}
练习题目
YY的gcd
gcd(x,y)为质数的区间数点
令
然后
求的就是
令 \(k =i\times d\)
枚举\(k\),
令
考虑线性筛\(f\)
-
k为质数，\(f(k)=\mu(\frac{k}{k})=\mu(1)=1\)
-
k有多个最小质因子，令\(y\)为k的最小质因子，\(z=\frac{k}{y}\)
- z没有多个因子，仅当枚举到\(d=y\)时，\(\mu(\frac{k}{d})=\mu(i)\)不为0，其余为0，\(f(x)=\mu(z)\)
- z有多个因子，都为0，\(z\)的情况等同于\(k\)的情况，为了方便统计还是令\(f(x)=\mu(z)\)
-
k只有一个最小因子
对于每一个\(\mu(\frac{k}{p})=\mu(\frac{z\times y}{p})\)
而\(z \text{ mod } y =0\)
根据\(\mu\)的定义有\(\mu(\frac{k}{p})=-\mu(\frac{z}{p})\)，而且多了一项\(\mu(i)\)
所以线性筛出\(f\)的前缀和，然后数论分块就行了
约数个数和
首先有一个公式：
好像是有什么映射关系吧。。。避免统计重复
这里可以归纳成一个trick：枚举某个枚举的数的因子的时候可以将后面的sigma提前，枚举后面的数，前面的数的个数就可以直接计算出来了
然后枚举\(x\)和\(y\)，设
显然有：
然后有
普通的莫反题这里就结束了，因为g很容易求出
这题里的g怎么求呢？
变换一下：
然后处理一下前缀和就可以\(O(1)\)求了
答案是\(f(1)\)
