CF765F Souvenirs

CF765F Souvenirs 题解

神题！！！

题意简述：给一个序列\(a\)，每次查询\([l,r]\)内\(|a_i-a_j|_{min},i,j\in[l,r]\)且\(i\not =j\)，不带查询。

数据范围：\(1\le N\le 10^5,1\le m \le10^5,0\le a_i\le 10^9\)。

Solution

方法一：

我们发现这个条件好眼熟，想想我们之前做过的题目AcWing 136. 邻值查找，这道题在蓝书上出现过。

让我们简单回忆一下做法，我们发现，对于每个点，它只可能和它的前驱/后继更新答案，所以我们只需找到一种快速查询前驱后继的数据结构就可以维护了。

这种事情平衡树很擅长，我们用一个 std::set，来每次找前驱和后继就行了。

同时在蓝书中，lyd曾介绍了一种使用链表的做法，具体做法是，我们先将数组排序，在建好链表，每次查完一个删除一个，链表插入/查前驱后继的时间复杂度为\(O(1)\)，非常优秀。

我们迁移到这道题上，由于链表每次只能插入和删除一个元素，又有若干个区间查询，并且不带删，还不要求强制在线，自然而然的想到莫队（快把莫队写到你脸上了）。

我们发现莫队移动端点是\(O(N\sqrt N)\)的，不太好用 std::set 维护，于是我们考虑使用链表。

同时，我们又发现对于每次加入操作，我们能很轻松的维护最大值，但是对于一个已有的链表，我们却无法直接快速的找到他的最大值。

对于这种插入好做的数据结构，我们可以联想到莫队的变种回滚莫队（不删除莫队）。

我们将每个询问分成两个部分，第一部分是左端点所在的块，第二部分是询问的另一半。

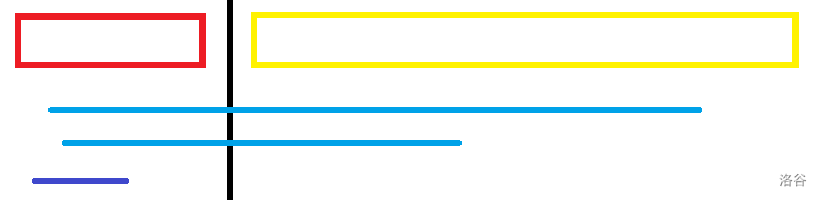
显然答案为左半段的贡献（红色），右半段的贡献（黄色），左半段到右半段的贡献三者中的最小值。

对于深蓝色的询问，我们暴力计算，对于浅蓝色的询问，我们考虑维护。

• 对于左半段的贡献，我们每次暴力跑就行了因为总长不超过\(O(\sqrt N)\)。

• 对于右边的贡献，我们将左端点相同的询问放在一起考虑，将这些询问按照右端点排序后离线一起做即可，跑一次\(O(N)\)。由于这是莫队，我们只会跑\(O(\sqrt N)\)次，所以总的时间复杂度为\(O(N\sqrt N)\)。

• 对于左半段到右半段的贡献，我们在跑贡献的时候维护重构维护就行了。

我们发现对于操作一和操作三，我们可以放在一起做，这样总的时间复杂度为\(O(N\sqrt N)\)。

简述一下我们要做的事情。

离散化+初始化链表+初始化莫队。

将询问按左端点所在块的编号分组，对于每组询问，按右端点排序。

依次处理每组询问，像普通回滚莫队一样维护右半段，重构左端点所在块算出左半段的贡献+左半段对右半段的贡献。

将左半段删掉，再做一次维护出右半段的贡献。

有点抽象，不过也不是不可做，看看可爱的代码吧。

这种拆贡献的思路很妙，有点像大分块题统计答案一样，考虑块对块的贡献，块对散块的贡献，散块对散块的贡献。

像这样合并两个区间的题目，如果我们发现要重构其中的一个区间，不妨试试回滚莫队。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=3e5+10,T=500;

pair<int,int>bot[N];
int L[N],R[N],pos[N],len,t;
int n,m,res[N],ans[M],val[N],a[N];
struct Query{int id,l,r;};
vector<Query>q[T];

struct List{
    int pre[N],nxt[N];
    void init(int n){
        for(int i=1;i<=n;i++)pre[i]=i-1,nxt[i]=i+1;
        nxt[0]=1,pre[n+1]=n;
    }
    void del(int x){
        pre[nxt[x]]=pre[x],nxt[pre[x]]=nxt[x];
    }
    int insert(int x){
        pre[nxt[x]]=nxt[pre[x]]=x;
        int ret=0x3f3f3f3f;
        if(pre[x]!=0)ret=min(ret,val[x]-val[pre[x]]);
        if(nxt[x]!=n+1)ret=min(ret,val[nxt[x]]-val[x]);
        return ret;
    }
}List;

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),bot[i]={a[i],i};
    sort(bot+1,bot+n+1);
    for(int i=1;i<=n;i++)a[bot[i].second]=i,val[i]=bot[i].first;
    len=sqrt(n),t=(n+len-1)/len;
    for(int i=1;i<=t;i++)L[i]=(i-1)*len+1,R[i]=min(i*len,n);
    for(int i=1;i<=t;i++)
        for(int j=L[i];j<=R[i];j++)
            pos[j]=i;
    scanf("%d",&m);
    for(int i=1,x,y;i<=m;i++){
        scanf("%d%d",&x,&y);
        q[pos[x]].push_back({i,x,y});
    }
    List.init(n);
    memset(ans,0x3f,sizeof(ans));
    for(int c=1;c<=t;c++){
        sort(q[c].begin(),q[c].end(),[](const Query&a,const Query&b){
            return a.r<b.r;
        });
        int posL=L[c],posR=R[c];
        for(int i=n;i>=posL;i--)List.del(a[i]);
        int p=posL-1;
        for(auto&tmp:q[c]){
            while(p<tmp.r)List.insert(a[++p]);
            int k=min(posR,tmp.r);
            for(int i=posL;i<=k;i++)List.del(a[i]);
            for(int i=k;i>=tmp.l;i--)ans[tmp.id]=min(ans[tmp.id],List.insert(a[i]));
            for(int i=tmp.l-1;i>=posL;i--)List.insert(a[i]);
        }
        while(p<n)List.insert(a[++p]);
        for(int i=posL;i<=posR;i++)List.del(a[i]);
        for(int i=n;i>posR;i--)List.del(a[i]);
        res[posR]=0x3f3f3f3f;
        for(int i=posR+1;i<=n;i++)res[i]=min(res[i-1],List.insert(a[i]));
        for(auto&tmp:q[c])
            if(tmp.r>posR)ans[tmp.id]=min(ans[tmp.id],res[tmp.r]);
    }
    for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
    return 0;
}

其实将链表换成0/1 trie也可以，它们两个都是插入好做删除难做。

方法二：