ARC117E Zero-Sum Ranges 2 题解

ARC117E Zero-Sum Ranges 2 题解

没想到这么妙的 dp 思路，写篇题解记录一下。

题意简述：给你 \(n\) 个 +1 ，\(n\) 个 -1 。求子区间和为 0 有 \(m\) 的为 \(2n\) 的序列有多少个。

数据范围：\(1 \le n \le 30\) ， \(1\le m \le N^2\) 。

Solution

一开始我们注意到数据范围很小，于是先想想如何乱搞。但是强制要求有 \(K\) 个区间和为 0 的子区间。这个限制启发我们使用 DP 。统计数量。

我们先考虑如何设计出一个状态，我们发现我们当前填了几个数和当前区间和为 0 有多个这两信息比较关键。我们不妨先设 \(f(i,j)\) 表示当前填了 \(i\) 个数，有 \(j\) 个区间和为 0 ，的总方案数。

如果我们想要转移，假设往下放一些连续的 -1 或 +1 ，我们无法进一步得知更新过后的 \(j\) ，所以我们设计出的这个状态无法转移。于是我们想想如何才能知道前面的序列的一些信息。

直接用 01 串维护是不现实的，单这一位的状态就有 \(2^{60}\) ，无法满足要求。

如果你做题比较多比较杂，你可能会想到用 std::vector 记录 +1 的段的左右位置。这样做有两个弊端，一是可能状态数过多（没算，但前两位就已经很多了）。二是这样做也无法确定前缀的和从而更新 \(j\) 。

我们的思路陷入的僵局。该考虑题目本身的性质。当你发现题目的操作简单，但是对方案计数时，可以考虑考虑画图（网格图、平面直角坐标系）。

经过画图，我们有如下性质。（图片来源于 Atcoder 官方题解）

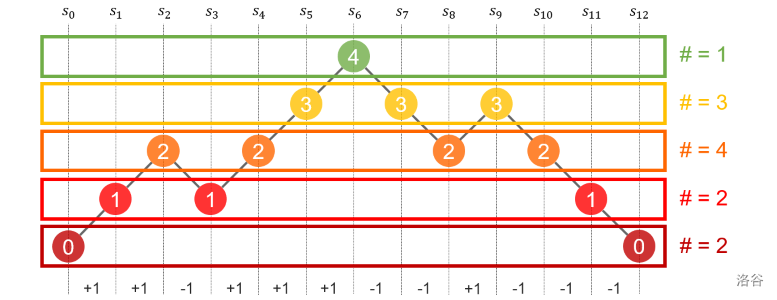
首先，我们发现，无论我们怎么画图， 它的起点和终点都是定的。所以我们只用考虑填了多少数，不用考虑填了什么数。（这是无关紧要的，因为只有恰好 \(n\) 个 +1 和 \(n\) 个 -1 ，才能回到原点）。

其次，我们发现，一个区间的和如果为 0 ，那么它们在图中是同一层的的部分。或许，我们将按顺序枚举改为按层枚举。那么每层对 \(j\) 的贡献就是 \(\binom{x}{2}\) 。

紧接着，我们考虑如何将层数这个东西放在状态里，如果直接放肯定是不行的，因为不是所有的间隙都能被插入一些数（有些中间有东西了，不能 -2）。

什么？只能插在间隙里？那么把间隙放在状态里！！！

我们设计 \(f(i,j,k)\) 表示当前填了 \(i\) 个数，和为 0 的区间有 \(j\) 个，有 \(k\) 个空隙（也可以设计为有 \(k\) 个连续段，转移方程有细微不同）的方案数。

这个东西叫连续段 DP ，对于这类题目（按层转移，插入数到一些空隙中），我们通常可以使用这样的转移方程使用 DP 解决。

我们假设下一层放 \(x\) 个，和为 0 的区间多了 \(\binom{x}{2}\) 个，间隙的数量变为 \(x-k-2\) 。

为什么是 \(x-(k+2)\) 呢？

我们要让最后的起点和终点在 \(x\) 轴上，左边右边必须放，且对间隙数没有贡献。

\(x\) 个元素最多有 \(x+1\) 个间隙，从画图可以得知，上一层每个连续段都会让间隙数 -1 。

所以新一层的间隙数为 \((x-2)+1-(k+1)=x-k-2\) 。

同时，将 \(x\) 个元素放入 \(k+2\) 个空隙中，根据插板法，一共 \(x-1\) 个能插板的位置，插入 \(k+1\) 个板分为 \(k+2\) 个组（含左右两边），方案数要乘上 \(\binom{x-1}{k+1}\) 。

所以我们写出状态转移方程：

\[f(i+x,j+\binom{n}{2},x-k-2)=\binom{x-1}{k+1}\cdot f(i,j,k) \]

这个状态转移方程只能处理之在 \(x\) 轴之上的方案。我们最后的答案只需将上下两边合并就可以了，即：

\[\sum f(i,j,k)\cdot f(2*n+1-i,m-j,k-1) \]

代码如下：

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=110,M=2e3+10;

int n,m;
ll C[N][N],f[N][M][N];

void init(int n=N-1){
    C[0][0]=1;
    for(int i=0;i<=n;i++){
        C[i][0]=C[i][i]=1;
        for(int j=1;j<i;j++)
            C[i][j]=C[i-1][j]+C[i-1][j-1];
    }
}

int main(){
    // freopen("test.in","r",stdin);
    // freopen("test.out","w",stdout);
    init();
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n+1&&C[i][2]<=m;i++)
        f[i][C[i][2]][i-1]=1;
    for(int i=1;i<=n*2+1;i++)
        for(int j=0;j<=m;j++)
            for(int k=0;k<=n;k++)
                for(int x=k+2;i+x<=n*2+1&&x<=n+1;x++){
                    if(j+C[x][2]>m)continue;
                    f[i+x][j+C[x][2]][x-(k+2)]+=C[x-1][k+1]*f[i][j][k];
                }
    ll ans=f[2*n+1][m][0];
    for(int i=1;i<=n*2+1;i++)
        for(int j=0;j<=m;j++)
            for(int k=1;k<=n;k++)
                ans+=f[i][j][k]*f[n*2+1-i][m-j][k-1];
    printf("%lld\n",ans);
    return 0;
}