2024.2.23 模拟赛 T1 题解

2024.2.23 模拟赛 T1 题解

题意简述：给一张 \(n\times m\) 的网格，每个格子都有一个权值。求用下面的管道让剩下的点构成闭合回路的最大权值。有一些格子不能放置管道，剩下的都要放置管道。闭合回路的权值定义为回路中拐角的点的权值之和。闭合回路不要求联通。

数据范围： \(1\le n\le150\) ， \(1\le m \le 30\) ， \(0\le a_{i,j}\le 100\) ， \(g_{i,j}\in\{0,1\}\) 。

Solution

第一眼看到闭合回路问题，考虑使用 插头 dp 。但数据范围显然不支持这个做法。

这个数据范围不太像状压或搜索（ \(n,m\) 都很小），又不太像小清新数据结构的数据范围（ \(n,m\) 都很大，为线性或亚线性算法）。

这种数据范围有很大概率是高维度的 dp 或网络流。

我是 dp 低手，不保证有 dp 做法能通过这道题。考场上考虑网络流解决这个问题。

这道题可以抽象为两个限制：1. 让管道成为一个闭合回路，2. 让权值最大。

最大流和最小割的建图方式无法让权值最大的同时满足管道形成闭合回路。我们考虑费用流。

我们直接判断闭合回路是不好做的，我们考虑闭合回路的性质。题目中给定的管道的度数都为 2 。我们手膜几个样例，发现有一个等价性质。

一组方案合法当且仅当找不到一个格子连出去的边撞到墙。

其实就是找不到这类情况：

或者是连到了一个非法的位置。

在费用流的学习过程中，我们有一个这样的建图潜意识：

我们要让满足题目限制条件的每一种情况对应一种最大流的情况，再让费用最大或最小。

在这张图中，我们还没确定源点和汇点。网格图中通常有两种建图方式。

1. 从 \((1, 1)\) 出发，只能向下或向右，到达 \((n, m)\) 。

2. 对图染色，将其中一种颜色连接源点，将另一种颜色连接汇点。

我们发现，一个闭合回路无法确定一个很好的方向，先搁置这个建图方法。

考虑将图黑白染色，上文中给出的性质是由两个相邻的格子产生的，这两个格子正好满足一黑一白。

于是我们有一种很直接的建图思路：（考场上的初期想法）

考虑拆点。黑格子流入，白格子流出。

我们要做这样的事情：黑色的格子通过情况选择流量的方向，白色的格子接受黑色格子的流量确定情况。

我们将流量按六种情况建好图，当流量为点数时，表明这是一个合法的闭合回路。

再附上权值，这很好做。

一开始我们想：将格子拆为六种情况，连向旁边的格子就行了。

我们发现黑色的格子是很好设置流量的方向，但是白色的格子无法正确的根据黑色的格子确定这个白色各自的流量并附上权值。

将每个格子新建四个方向的新点，让每种情况先连接新点，这样我们就能很好的确定白色格子的形状。

但是这样有一个潜在的问题：如果我们只在六种情况中选一个，一个常规的建图方式是新建一个点，将这个点连向六种情况，流量为 1 ，再只将新点流入一个流量，这样做是肯定正确的。

但是在这道题中不是这样，确定一种情况后，这个点的流量只为 1，但是我们需要两个流量确定白色的格子的形态。

如果我们将上述所有的边流量全设为 2 ，又无法将黑色格子确定一个唯一的情况。

我们考虑更换确定权值的方法。要求每种情况中向四个方向中的两个流出的流量为 1 。

我们发现，只有拐角的情况能产生贡献，就是出现 \(90^{\circ}\) 的情况。（拐角型）

同时 \(180^{\circ}\) 没有贡献。（直线型）

也就是说，对于每个拐角型/直线型，他们是等价的，我们应该放在一起考虑。

手玩一下发现，下面的这种情况包含全部的拐角型，边权为流量。

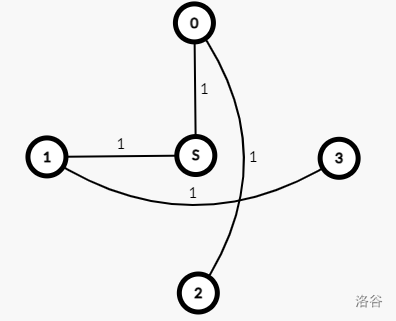
当它变为直线型时，其中的一条边旋转了 \(90^{\circ}\) 。一定经过下图加粗的边，设费用为点权，即为换边的代价：

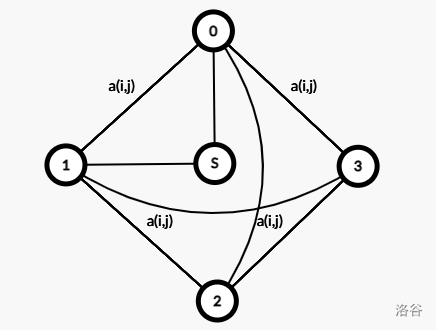
将黑点和白点的建图方式换为这一种，就完成了这道题。

总建图过程：

将图黑白染色。

对于每个点，新建四个方向上的新点。

对于黑点，先从源点连接任意两个相邻方向的点，再连接两组对称点，如图。流量为 1 ，费用为 0 。

再连接任意相邻两个方向的新点，流量为 1，费用为 \(a_{i,j}\) 。

对于白点，将上述黑点的建图方向取反。就是先从两个相邻方向的点连接到汇点，再连接两组两组对称点。流量为 1 ，费用为 0 。

再连接任意相邻两个方向的新点，流量为 1，费用为 \(a_{i,j}\) 。

将两个相邻格子中的对应方向相连。从黑点的新点连到白点的新点，流量为 1，费用为 0 。

跑最小费用最大流，将总总费用减去最小费用得到答案。

当流量为点数时，表明每个点都按照要求流出了两个流量，接受了两个流量。

如果不相等，那么原问题无解，输出 -1 .