dp优化trick

dp 优化 trick

dp 是算法竞赛的常见考点，有时题目的难度不在于设计状态或写出 dp 的状态转移方程，而是把出题的重心放在对 dp 的优化上。

这类题目类型很多，并且有相对常见的套路，适合应付老师的要求，下面一起来总结一下：

P.S. 本文没有详细的 dp 状态转移方程的推导过程，重心主要在优化上。

1. 前缀和优化

这时一个非常常见的套路，如果我们写出 dp 的状态转移方程，发现式子形如：

\[f(x)=\sum_{i=l}^r f(i) \]

如果我们新维护一个式子 \(g(x)=\sum_{i=1}^nf(i)\) ，用 \(g(r)-g(l-1)\) 代替上面式子的计算。

我们就可以减少枚举求和的重复性工作，将它的时间复杂度优化一个 \(O(n)\) 。

比如 11.16 模拟赛 T3 ，如果贪心做完了每行或每列的贡献，将它排序后求前和，就可以将计算答案的时间复杂度优化一个 \(O(K)\) ，每次求答案的过程就变成 \(O(1)\) ，可以通过这道题。

2. 单调栈/单调队列优化

通常 dp 式子中的某维可以写成 \(f(i)=\max \{f(j)_+val(i,j)\}\) 的形式。

如果我们可以将它们中分为只关于 \(i\) 的部分 \(a(i)\) 和只关于 \(j\) 的部分 \(b(i)\) 。

与此同时，我们发现决策集合在序列上的移动是单调的，我们通常可以使用单调队列优化/单调栈优化。

有时最优决策在队头，我们需要新开一个数据结构来维护它们。

蓝书上的题目：裁剪序列。

题意简述：将序列分为若干段，在每段的和不超过 \(M\) 的前提下让每段最小值之和最小，序列中的所有元素非负。

我们设 \(f(i)\) 强制钦定最后一段的结尾为 \(i\) ，维护最小值之和。

容易发现，由于序列中的元素非负，所以我们可以用单调队列维护上一个转移的决策集合。

左右端点都是单调递增的，但是我们要找的最优决策不一定是队头。

此时，我们需要一个支持插入删除维护最小值的数据结构同步维护单调队列中的元素。

使用 std::set 足矣，每次和单调队列维护决策时同步在 std::set 中插入删除。每次取最小值转移。

还挺套路的，决策的在序列上的移动是单调的时候我们直接使用单调队列即可。

3. 四边形不等式优化（决策单调性优化）

这种这能在考场上灵光一现想到，一般用打表的方式找到最优决策的单调性，在使用决策单调队列优化。

很多人不知道这个东西是怎么用的，简述一下：

设 \(g(i)\) 为 \(f(i)\) 的最优决策，有时它是单调递增的（决策单调性）。

我们可以用队列维护它的决策最优，每次更新决策时与队尾比较那个决策更优。（弹出队尾）

转移时二分出一个位置转移，由于决策单调性，我们前面的决策没必要保留，让它出队。（转移+弹出队头）

我们发现这和单调队列很像，实际上取队头为最优决策的单调队列都可以用四边形不等式优化。P.S. 实际上反向优化了，\(O(n)->O(nlogn)\)。

这个东西适合在写出式子发现几乎无法优化的时候，用打表的方式找一找有没有决策单调性，再用四边形不等式优化。

通常在最后，发现 dp 式子 \(f(i)=\max\{f(j)+val(i,j)\}\) 中 \(val(i,j)\) 是一个高次乘积项的时候通常满足四边形不等式。

比如：诗人小G，dp 式子是\(f[i]=min_{0\le j<i}\{f[j]+|(s[i]-s[j])+(i-j-1)-L|^p\}\)，我们先写暴力，发现时间暴了，考虑优化。

我们通过打表容易发现这个东西有决策单调性，直接上四边形不等式优化 dp 即可。

更详细的证明戳这里，可能不太严谨。

4. 斜率优化

dp 式 \(f(i)=\max {f(j)_+val(i,j)}\) 有时候 \(val(i,j)\) 是 \(i,j\) 的一次乘积项。

我们有更优秀的做法。

我们将 dp 式子化成直线的形式，转化为线性规划问题，一个非常板子的题目：P3628 [APIO2010] 特别行动队。

题意简述：给定一个序列 \(A\)，找到一些连续子串，每个子串 \([l,r]\) 的贡献为 $$aX^2+bX+c$，X为 \([l,r]\) 区间和，求最大贡献。

状态转移方程：

\[f(i)=\max_{1\le j<i}f(j)+a\times(s_i-s_j)^2+b\times (s_i-s_j)+c \]

回忆单调队列优化 dp，我们实质上是在维护一个决策集合，将i看做定值，维护只与j有关的多项式 \(val(j)\) ，及时排除掉不可能作为最有决策的取值。

通常我们将与i有关的项看做常量，将与j有关的项看做变量，然后根据多项式 \(val(j)\) 的单调性来排除冗余情况。

我们将这个思想沿用到这里，将与i有关的项看做常量，将与j有关的项看做变量。

化成直线式：

\[f(j)+bs_j^2-bs_j=2as_is_j+f(i)-as_i^2-bs_i-c \]

有了这个有什么用呢？
将它们画在笛卡尔坐标系上，仔细思考，我们在坐标系上寻找最优决策实际上是给定一个斜率，让 f(i) 所在的 b(i) 最大。

我们从上往下平移这条给定斜率的直线。

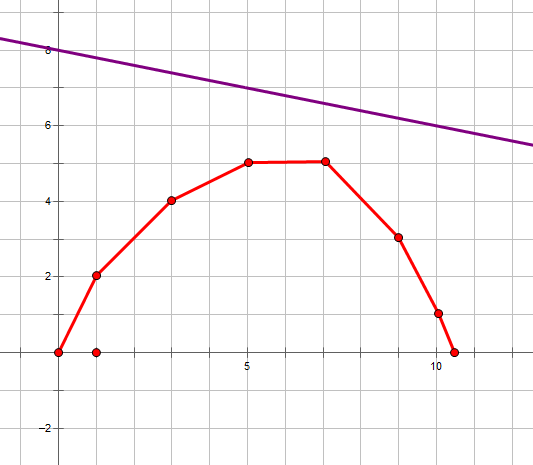
我们碰到的第一个点就是最优决策。

通过观察图像性质，可以发现，可以成为最有决策当且仅当这个点在所有点构成的点集的凸包上。

上凸包上相邻两点的斜率递增，下凸包反之。

于是可以维护斜率 \(k(i)=2as_i\)，单调递增，形如单调队列，只留下可行决策。

同时，由于此题定斜率 \(k(i)=2as_i\)一定满足单调递增，所以所有小于当前斜率的直线以后也一定不能成为最优决策，可以从队头出队。P.S.这个不是所有斜率优化 dp，都能使用，如果定斜率不满足单调性，需要用二分找到最优决策。

5. 数据结构优化

1. 线段树

如果决策集合在区间上并且维护的信息是可以直接用线段树快速找到的，那么可以直接使用。

有比较显然的题目 清理班次2：\(f(i)=\min_{j=1}^{i-1}{f_j}+c_i\)。线段树单点修+区间查最小值即可（算是板子吧）。

另一道题目：11.19 模拟赛 T2。

有很多人忘了这道题目，重述一下题面：将序列划分为长为 1 或 2 的段，贡献为元素权值和。求最小级差。

容易想到暴力，钦定最小值，再用 dp 求出在限制下的最小的最大值，时间复杂度是 \(O(n^2)\)。

但这个信息可以直接用线段树来做，多打几个标记，设 \(tag(l,r,0/1,0/1)\) 表示线段树上区间
\([l, r]\) 内部已经全部覆盖，覆盖 \(l\) 的区间左端点是否为 \(l\)，覆盖 \(r\) 的区间右端点是否为 \(r\)。

合并很好做，枚举 \(mid\) 和 \(mid+1\) 的颜色 \(z\in \{0,1\}\)，在线段树内暴力合并，\(tag(l,r,x,y)=min_{z\in\{0,1\}}\{max\{tag(l,mid,x,z),tag(mid+1,r,z,y)\}\}\) 。

每次枚举最大值，会有一些端点无法贡献答案（小于限制），单点将它修改成 \(+\infty\) 即可。

2. 树状数组

适用范围是线段树的真子集，在维护的信息是一个前缀时可以代替线段树做到更小的常数。

方伯伯的玉米田：贪心每次拔最高的玉米，有：

\[f(i,j)=max\{f(i',j')+1\},i\in[1,i),j\in[1,j),h(i')+j\le h(i)+j \]

我们直接转移是 \(O(n^4)\) 的，考虑优化，反过来枚举 \(j\) 让贡献不会互相影响。

把状态放在二维平面上，发现我们每次都在求一个最上角的最值，直接上二维树数组维护即可。

3. 其他数据结构优化（关于决策集合维护方式的数据结构优化）

如果 dp 间的转移有很多的限制，考虑使用 CDQ 分治 来解决问题。

通过排序+分治+指针线性扫描优化掉一些限制，让他们之间可以互相转移。

由于这不是 NOIP 的考试范围，并且你现在在备战 NOIP ，所以你不需要深入了解这种做法。

这个东西很有启发性，启发我们可以根据数据结构的性质来维护决策集合，让它能直接转移。

6. 矩阵快速幂加速线性递推

当转移 “重重叠叠” 时，比如我们不断的再用之前的 \(f(j)\) 进行转移，可以考虑将它们转化为矩阵模型进行转移。

比如一道很好的题目：美食家：恰好 \(T\) 天回到节点 1 ，很像矩阵加速递推能干的事情。

尝试写一下状态转移方程：

\[f(k,i,j)=\max_p\{f(k-1,i,p)+G(p,j)\} \]

其中 \(G\) 是邻接矩阵，我们定义广义矩阵乘法 \(C_{i,j}=\max\{A_{i,k}+B_{k,j}\}\) 。

所以做 \(k\) 次矩阵乘法 \(f_k=f_0\times G^k\) 。

但是我们每次都跑一边明显会 T ，所以我们可以像 ST_table 一样维护 \(G^{2^k}\) 的矩阵转移即可。

这个东西貌似不再 NOIP 考纲范围内，考也应该不会考的太难，简单带过一下。

7. 拉格朗日插值优化

所谓插值，就是给定一个 \(n+1\) 个点，这些点能确定一个唯一确定最高次项为 \(n\) 的多项式 \(A(x)\)，我们要求 \(A(k)\) 的值。

我们有拉格朗日插值：

\[A(k)=\sum_{i=0}^ny_i\prod_{i\not =j}\frac{k-x_j}{x_i-x_j} \]

设 \(x=x_i, y=y_i\) 带入证明一下：

\[A(x)=\sum_{i=0}^ny_i\prod_{i\not =j}\frac{x-x_j}{x_i-x_j} \]

观察式子，我们发现第一层循环中，当 \(x_i\not=x\) 时，在第二层循环中都有一个 \(x_j=x\) 让分母等于 0。

所以只有当 \(x_i=x\) 是才会产生贡献，原式等价于：

\[A(x)=y\prod_{i\not=j}\frac{x-x_j}{x-x_j} \]

所以有 \(A(x)=y\) 恒成立，同理可推在 \(A(k)\) 时所得到的值是正确的答案。

当 \(x_i\) 连续取到时，我们有更优秀的性质，当 \(x_i=i\) 时，带入可得：

\[A(k)=\sum_{i=0}^ny_i\prod_{i\not =j}\frac{k-j}{i-j} \]

离线处理一些东西：

\[pre_i=\prod_{j=0}^ik-j \]

\[nxt_i=\prod_{j=i}^n k-j \]

式子变为：

\[A(k)=\sum_{i=0}^n\frac{pre_{i-1}\times nxt_{i+1}}{(i-1)!\times (n-i)!} \]

还是挺显然的，离线处理一下就是 \(O(n)\) 了。

P3643 [APIO2016] 划艇：

如果你提前做一些拉格朗日插值的板子，你一定见过形如这样的式子：\(\sum_{i=1}^ni^k\) 。

有一个不太好证明的结论，这是一个 \(k+1\) 次多项式，CF622F。

它们大致有一个共同的性质：\(f_i(x)=C,f_i(x)=\sum_{j=1}^xf_{i-1}(jd)\)（若干次前缀和）。

对于这道题，我们简单列一下式子，设 \(f(i,j)\) 表示前 \(i\) 个元素中可选可不选，最后一个元素的值为 \(j\) ，状态转移方程为：

\[f(i,j)=f(i-1,j)+[a_i \le n \le b_i]\sum_{k=1}^{j-1}f(i-1,k) \]

然后直接上拉格朗日插值即可。

8. DDP

我们将每个序列上的元素看成一个矩阵，再用数据结构维护这个东西。

通常是单点修+区间查，这时线段树已经足够了。

动态最大子段和：朴素的状态转移方程是 \(f(i)=\max\{a_i,f(i-1)+a_i\}\)。

我们将它改写成矩阵形式：

\[\begin{bmatrix} a_k & a_k\\ -\infty & 0 \end{bmatrix}\begin{bmatrix} f_{k-1} \\ 0 \end{bmatrix}=\begin{bmatrix} f_k \\ 0 \end{bmatrix} \]

然后用线段树维护矩阵就行了，这就是一个板子。

有时候这个问题放在树上，这时我们就需要使用树上数据结构进行维护。

9. 其他瞎搞

[ABC315F] Shortcuts

容易发现我们跳过点的惩罚太高了，是指数级别，所以我们最多跳 30 次。

有了这个性质以后我们就直接做转移就行了：

\[f(i,k)=f(i-1,k)+dist(i-1,i) \]

\[f(i,k)=(j,k-(i-j-1))+dist(i,j) \]

这种题我们需要观察状态转移方程，优化 dp。

总结

1. 我们可以从维护决策集合的角度维护决策集合。

如果 \(val(i,j)\) 可以拆成只关于 \(i,j\) 的部分，我们使用单调队列优化。

如果 \(val(i,j)\) 是 \(i,j\) 的一次乘积项，我们化成直线式，使用斜率优化即可。

如果决策集合可以用数据结构直接优化，我们就可以直接使用数据结构维护。

否则答辩找规律，如果有决策单调性就用四边形不等式优化 dp。

2. 我们可以加快转移的速度。如果状态可以直接化成矩阵式，用 DDP 或 快速幂加速递推。

3. 最后，我们直接瞪眼，使用前缀和优化。多次前缀和使用拉格朗日插值优化，否则就直接瞎搞。