斜率优化dp

斜率优化 dp

前言：一个非常套路的 dp 优化方法。

前置知识：单调队列优化 dp

例题1

一个非常板子的题目：P3628 [APIO2010] 特别行动队

题意简述：给定一个序列\(A\)，找到一些连续子串，每个子串\([l,r]\)的贡献为\(aX^2+bX+c\)，\(X\)为\([l,r]\)区间和，求最大贡献。

数据范围：\(1 \leq n \leq 10^6\)，\(-5 \leq a \leq -1\)，\(-10^7 \leq b \leq 10^7\)，\(-10^7 \leq c \leq 10^7\)，\(1 \leq A_i \leq 100\)。

Solution

定义\(f(i)\)为最后一个连续子串以\(i\)结尾的最大贡献，容易写出状态转移方程。

\[f(i)=\max_{1\le j<i}f(j)+a\times(s_i-s_j)^2+b\times (s_i-s_j)+c \]

时间复杂度为\(O(n^2)\)，考虑优化。

观察状态转移方程，可以发现出现了\(i,j\)乘积项，不好进行拆分+单调队列优化。

先不看\(max\)，展开式子：

\[f(i)=f(j)+as_i^2+bs_j^2-2as_is_j+bs_i-bs_j+c \]

回忆单调队列优化 dp，我们实质上是在维护一个决策集合，将\(i\)看做定值，维护只与\(j\)有关的多项式\(val(j)\)，及时排除掉不可能作为最有决策的取值。

通常我们将与\(i\)有关的项看做常量，将与\(j\)有关的项看做变量，然后根据多项式\(val(j)\)的单调性来排除冗余情况。

我们将这个思想沿用到这里，将与i有关的项看做常量，将与j有关的项看做变量。

然后我们发现，通过移项，这个式子可以变为形如\(y=kx+b\)的形式，其中\(x,y\)是与\(j\)有关的项，\(k,b\)是与\(i\)有关的项。

\[f(j)+bs_j^2-bs_j=2as_is_j+f(i)-as_i^2-bs_i-c \]

所以：

\[y(j)=f(j)+bs_j^2-bs_j \]

\[x(j)=s_j \]

\[k(i)=2as_i \]

\[b(i)=f(i)-as_i^2-bs_i-c \]

有了这个有什么用呢？

将它们画在笛卡尔坐标系上，仔细思考，我们在坐标系上寻找最优决策实际上是给定一个斜率，让\(f(i)\)所在的\(b(i)\)最大。

我们从上往下平移这条给定斜率的直线。

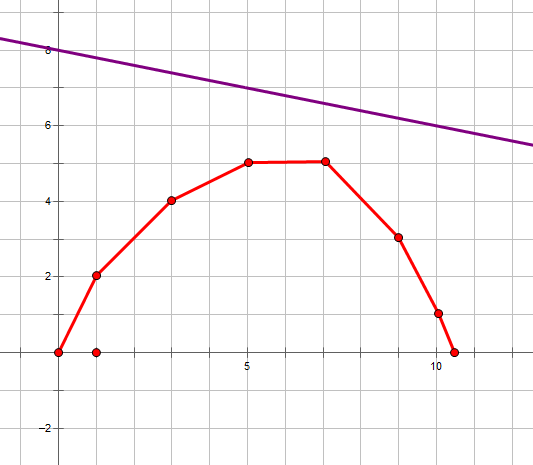
我们碰到的第一个点就是最优决策。

通过观察图像性质，可以发现，可以成为最有决策当且仅当这个点在所有点构成的点集的凸包上。

上凸包上相邻两点的斜率递增，下凸包反之。

于是可以维护斜率\(k(i)=2as_i\)，单调递增，形如单调队列，只留下可行决策。

同时，由于此题定斜率\(k(i)=2as_i\)一定满足单调递增，所以所有小于当前斜率的直线以后也一定不能成为最优决策，可以从队头出队。P.S.这个不是所有斜率优化 dp，都能使用，如果定斜率不满足单调性，需要用二分找到最优决策。

代码如下：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;

int s[N],n,m,a,b,c,q[N],l=1,r=1,ans,f[N];
double slope(int i,int j){return ((f[i]-f[j])+(1.0*a*s[i]*s[i]-b*s[i])-(a*s[j]*s[j]-b*s[j]))/(2*a*s[i]-2*a*s[j]);}
int work(int i,int j){return a*(s[i]-s[j])*(s[i]-s[j])+b*(s[i]-s[j])+c;}

signed main(){
    scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
    for(int i=1;i<=n;i++)scanf("%lld",&s[i]),s[i]+=s[i-1];
    for(int i=1;i<=n;i++){
        while(l<r&&slope(q[l],q[l+1])<s[i])l++;
        f[i]=f[q[l]]+work(i,q[l]);
        while(l<r&&slope(q[r-1],q[r])>slope(q[r],i))r--;
        q[++r]=i;
    }
    printf("%lld\n",f[n]);
    return 0;
}

例题2

另一个很板的题目：CF1715E Long Way Home

题意简述：给一张\(n\)个点，\(m\)条边的无向图，边有边权。可以进行\(k\)次传送，花费\((x-y)^2\)，求最短路。

Solution

又遇到了\(i,j\)的乘积项，考虑斜率优化。

我们考虑拆点分层图，但我们每次更新的时候都要都要将\(n\)个点全部加进来找到最优答案。

我们可以先每次更新最短路，在用斜率优化更新一遍。

现将\(n\)个点都加入集合，在不断根据斜率单调性优化。

板子题一道。

代码如下：P.S.隐式建图。

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=1e5+10,M=N*2;

int head[N],ver[M],nxt[M],tot=1;
ll edge[M];
void add(int x,int y,ll z){
    ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
}

int n,m,k;
bool v[N];
ll d[N],f[N],q[N],l,r;
priority_queue<pair<ll,int>>heap;
void dijkstra(){
    memset(v,0,sizeof(v));
    heap.push(make_pair(0,1));
    d[1]=0;
    while(heap.size()){
        int x=heap.top().second;heap.pop();
        if(v[x])continue;
        v[x]=1;
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i];
            if(d[y]>d[x]+edge[i]){
                d[y]=d[x]+edge[i];
                heap.push(make_pair(-d[y],y));
            }
        }
    }
}

double slope(ll x,ll y){
    if(x==y)return 1e18;
    return 1.0*(f[x]+x*x-f[y]-y*y)/(x-y);
}

int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),add(x,y,z),add(y,x,z);
    memset(d,0x3f,sizeof(d));d[1]=0;
    while(k--){
        dijkstra();
        for(int x=1;x<=n;x++)f[x]=d[x];
        l=r=1;q[1]=0;
        for(int i=1;i<=n;i++){
            while(l<r&&slope(q[r-1],q[r])>slope(q[r],i))r--;
            q[++r]=i;
        }
        for(int i=1;i<=n;i++){
            while(l<r&&slope(q[l],q[l+1])<2.0*i)l++;
            if(d[i]>f[q[l]]+(i-q[l])*(i-q[l])){
                d[i]=f[q[l]]+(i-q[l])*(i-q[l]);
                heap.push(make_pair(-d[i],i));
            }
        }
    }
    dijkstra();
    for(int i=1;i<=n;i++)printf("%lld ",d[i]);
    puts("");
    return 0;
}

总结

推出状态转移方程后，通过是否有\(i,j\)的乘积项进行分类。

• 如果没有\(i,j\)的乘积项，分离\(i,j\)，考虑单调队列维护决策集合。

• 如果有\(i,j\)的乘积项，移项为一次函数，考虑斜率优化维护决策集合。

• 更特殊的，如果\(i,j\)的乘积项次数大于等于\(2\)，考虑是否有决策单调性，运用四边形不等式优化。

同时，要考虑决策集合，用二分/数据结构优化加入/删除集合的时间复杂度。

本来还有一道题的，先鸽了qwq。