二分答案模板及二分答案问题讲解

二分答案

！阅读须知||阅读本博文前笔者认为读者已经学会（或了解）了： 
1.基础语言与算法 
2.标准二分法（二分思想） 
3.二分查找

定义

二分答案与二分查找类似，即对有着单调性的答案进行二分，大多数情况下用于求解满足某种条件下的最大（小）值。

答案单调性

 

答案的单调性大多数情况下可以转化为一个函数，其单调性证明多种多样，如下：

1. 移动石头的个数越多，答案越大（NOIP2015跳石头）。
2. 前i天的条件一定比前 i + 1 天条件更容易（NOIP2012借教室）。
3. 满足更少分配要求比满足更多的要求更容易（NOIP2010关押罪犯）。
4. 满足更大最大值比满足更小最大值的要求更容易（NOIP2015运输计划）。
5. 时间越长，越容易满足条件（NOIP2012疫情控制）。

可以解决的问题

1. 求最大的最小值（NOIP2015跳石头）。
2. 求最小的最大值（NOIP2010关押罪犯）。
3. 求满足条件下的最小（大）值。
4. 求最靠近一个值的值。
5. 求最小的能满足条件的代价。

代码

为了保证解在二分搜索的区间里，故不同的问题有着不同（但相似）的写法，读者可以画一个区间模拟一下~

题目解析

1.假定一个解并判断是否可行(POJ 1064)

链接：http://poj.org/problem?id=1064

Cable master

Time Limit: 1000MS Memory Limit: 10000K

Description

Inhabitants of the Wonderland have decided to hold a regional programming contest. The Judging Committee has volunteered and has promised to organize the most honest contest ever. It was decided to connect computers for the contestants using a "star" topology - i.e. connect them all to a single central hub. To organize a truly honest contest, the Head of the Judging Committee has decreed to place all contestants evenly around the hub on an equal distance from it. 
To buy network cables, the Judging Committee has contacted a local network solutions provider with a request to sell for them a specified number of cables with equal lengths. The Judging Committee wants the cables to be as long as possible to sit contestants as far from each other as possible.
The Cable Master of the company was assigned to the task. He knows the length of each cable in the stock up to a centimeter,and he can cut them with a centimeter precision being told the length of the pieces he must cut. However, this time, the length is not known and the Cable Master is completely puzzled. 
You are to help the Cable Master, by writing a program that will determine the maximal possible length of a cable piece that can be cut from the cables in the stock, to get the specified number of pieces.

Input

The first line of the input file contains two integer numb ers N and K, separated by a space. N (1 = N = 10000) is the number of cables in the stock, and K (1 = K = 10000) is the number of requested pieces. The first line is followed by N lines with one number per line, that specify the length of each cable in the stock in meters. All cables are at least 1 meter and at most 100 kilometers in length. All lengths in the input file are written with a centimeter precision, with exactly two digits after a decimal point.

Output

Write to the output file the maximal length (in meters) of the pieces that Cable Master may cut from the cables in the stock to get the requested number of pieces. The number must be written with a centimeter precision, with exactly two digits after a decimal point. 
If it is not possible to cut the requested number of pieces each one being at least one centimeter long, then the output file must contain the single number "0.00" (without quotes).

Sample Input

4 11
8.02
7.43
4.57
5.39

Sample Output

2.00

题目大意：有n条绳子，长度分别为L[i]。如果从他们中切割出k条长度相同的绳子的话，这k条绳子每条最长能有多长？（答案保留小数点后两位，规定1单位长度的绳子最多可以切割成100份）。

分析：二分搜索最大长度x。我们令C（x）为可以得到K条长度为x的绳子，那么问题就变为了求满足条件C（x）的最大的x。在区间初始化时，只需使用充分大的数inf（大于绳子的最大长度的二倍）作为上界即可：left=0,right=inf。那么现在的问题就变为了如何高效的判断C（x）是否满足。由于长度为L的绳子最多可以切割出floor(L/x)段长度为x的绳子，因子C（x）=floor(Li/x)的总和是否不小于k，他可以在O（n）的时间内判断出来。

AC代码：

#include <cstdio>
#include <cmath>
using namespace std;
const int M=10005;
const double inf=200005.0;
double L[M];
int n,k;
bool judge(double x)
{
    int num=0;
    for(int i=0;i<n;i++)
      num+=(int)(L[i]/x);
    return num>=k;
}
void solve()
{
    double left=0,right=inf;
    for(int i=0;i<100;i++) //代替while(r>l) 避免了精度问题
    { //1次循环可以把区间缩小一半，100次可以达到10^(-30)的精度
        double mid=(left+right)/2;
        if(judge(mid)) left=mid;
        else right=mid;
    }
    printf("%.2f\n",floor(right*100)/100);
}
int main()
{
    while(scanf("%d%d",&n,&k)!=-1)
    {
        for(int i=0;i<n;i++)
          scanf("%lf",&L[i]);
        solve();
    }
    return 0;
}

 

2.最大化最小值(POJ 2456)

链接：http://poj.org/problem?id=2456

 

Aggressive cows

Time Limit: 1000MS Memory Limit: 65536K 

Description

 

Farmer John has built a new long barn, with N (2 <= N <= 100,000) stalls. The stalls are located along a straight line at positions x1,...,xN (0 <= xi <= 1,000,000,000). 

His C (2 <= C <= N) cows don't like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, FJ want to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?

 

Input

 

* Line 1: Two space-separated integers: N and C 

* Lines 2..N+1: Line i+1 contains an integer stall location, xi

 

Output

 

* Line 1: One integer: the largest minimum distance

 

Sample Input

 

5 3
1
2
8
4
9

 

Sample Output

 

3

 

Hint

OUTPUT DETAILS: 
FJ can put his 3 cows in the stalls at positions 1, 4 and 8, resulting in a minimum distance of 3. 
Huge input data,scanf is recommended.

 

题意概述：农夫有c头牛，n个隔间，c头牛很躁动，很容易相互打架，因此农夫想把它们分得越远越好，要你分配隔间使得相邻两头牛的距离越远越好，问你这c头牛分割的最小距离的最大值。

解题思路：先对隔间的坐标排序，对于牛，最小距离是0，最大距离不会超过两端两头牛的距离值，因此二分地查找分割距离的最大值，每次mid都judge一次，judge的时候贪心地放置牛，保证前i头牛是符合这样分割标准的。（二分如果拿捏不好精度，最好就直接暴力100次。）

AC代码：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#define INF 0x7fffffff
#define maxn 100100
using namespace std;
int a[maxn];
int n, c;
 
int judge(int m)
{
    int last = 0;
    for (int i = 1; i < c; i++)
    {
        int cur = last + 1;
        while (cur < n && a[cur] - a[last] < m)
            cur++;
        if (cur == n)
            return 0;
        last = cur;
    }
    return 1;
}
int main()
{
    while (scanf("%d%d", &n, &c) != EOF)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &a[i]);
        sort(a, a + n);
        int l = 0, r = INF, m;
        for (int i = 0; i < 100; i++)
        {
            m = l + (r - l) / 2;
            if (judge(m))
                l = m;
            else 
                r = m;
        }
        printf("%d\n", l);
    }
    return 0;
}

 

3.最大化平均值(POJ 2976)

链接：http://poj.org/problem?id=2976

 

Dropping tests

Time Limit: 1000MS Memory Limit: 65536K

 

Description

In a certain course, you take n tests. If you get a_i out of b_i questions correct on test i, your cumulative average is defined to be

.

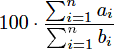Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.

Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is 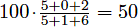. However, if you drop the third test, your cumulative average becomes .

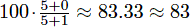Input

The input test file will contain multiple test cases, each containing exactly three lines. The first line contains two integers, 1 ≤ n ≤ 1000 and 0 ≤ k < n. The second line contains n integers indicating a_i for all i. The third line contains n positive integers indicating b_i for all i. It is guaranteed that 0 ≤ a_i ≤ b_i ≤ 1, 000, 000, 000. The end-of-file is marked by a test case with n = k = 0 and should not be processed.

Output

For each test case, write a single line with the highest cumulative average possible after dropping k of the given test scores. The average should be rounded to the nearest integer.

Sample Input

3 1
5 0 2
5 1 6
4 2
1 2 7 9
5 6 7 9
0 0

Sample Output

83
100

Hint

To avoid ambiguities due to rounding errors, the judge tests have been constructed so that all answers are at least 0.001 away from a decision boundary (i.e., you can assume that the average is never 83.4997).

 

题目大意：给定n个二元组(a,b)，扔掉k个二元组，使得剩下的a元素之和与b元素之和的比率最大。

题目求的是 max(∑a[i] * x[i] / (b[i] * x[i]))   其中a,b都是一一对应的。 x[i]取0,1  并且 ∑x[i] = n - k;

那么可以转化一下。  令r = ∑a[i] * x[i] / (b[i] * x[i])  则必然∑a[i] * x[i] - ∑b[i] * x[i] * r= 0；（条件1）

并且任意的 ∑a[i] * x[i] - ∑b[i] * x[i] * max(r) <= 0  (条件2，只有当∑a[i] * x[i] / (b[i] * x[i]) = max(r) 条件2中等号才成立)

然后就可以枚举r , 对枚举的r， 求Q(r) = ∑a[i] * x[i] - ∑b[i] * x[i] * r  的最大值，  为什么要求最大值呢？  因为我们之前知道了条件2，所以当我们枚举到r为max(r)的值时，显然对于所有的情况Q(r)都会小于等于0，并且Q(r)的最大值一定是0.而我们求最大值的目的就是寻找Q(r)=0的可能性，这样就满足了条件1，最后就是枚举使得Q(r)恰好等于0时就找到了max(r)。而如果能Q(r)>0 说明该r值是偏小的，并且可能存在Q(r)=0,而Q(r)<0的话，很明显是r值偏大的，因为max(r)都是使Q(r)最大值为0，说明不可能存在Q(r)=0了。

AC代码：

#include <iostream>
#include <string>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn=1002;
const double eps=1e-7;
int n,k;
double a[maxn];
double b[maxn];
int main()
{
    while(cin>>n>>k)
    {
        if(n==0&&k==0)
            break;
        for(int i=0; i<n; i++)
            scanf("%lf",&a[i]);
        for(int j=0; j<n; j++)
            scanf("%lf",&b[j]);

        double L=0.0;
        double R=1.0;
        double mid;

        double t[1004];

        while(R-L>eps)
        {
            mid=(R+L)*1.0/2;

            for(int i = 0; i < n; i++)
                t[i] = a[i] - mid * b[i];
            sort(t, t + n);
            double sum = 0;
            for(int i = k; i < n; i++)
                sum += t[i];

            if(sum>0)
                L=mid;
            else
                R=mid;
        }
        printf("%.0f\n",mid*100);
    }
    return 0;
}