Introduction to Geometry （Lectures 10~11）

Introduction to Geometry （Lectures 10~11）

内容：

• Examples of geometry
• Various representations of geometry
  • implicit geometry(隐式几何)
  • explicit geometry(显式几何)
• Many implicit Representations in Graphics
  • Algebraic surfaces
  • Constructive solid geometry
  • Level set methods
  • Fractals
  • ....
• Many explicit Representations in Graphics
  • 点云（point Cloud）
  • triangle meshes
  • Bezier surfaces
  • NURBS
  • subdivision surfaces
  • .......

Examples

不同形状的几何、曲线的表示：

水滴的描述：

复杂几何的表述:

(存储、渲染问题)

Various representations of geometry

implicit geometry 不给坐标给表达式

隐式的几何方法不会告诉点具体在哪，而说明点的满足的一定的关系。表示一定的关系并不给具体点。

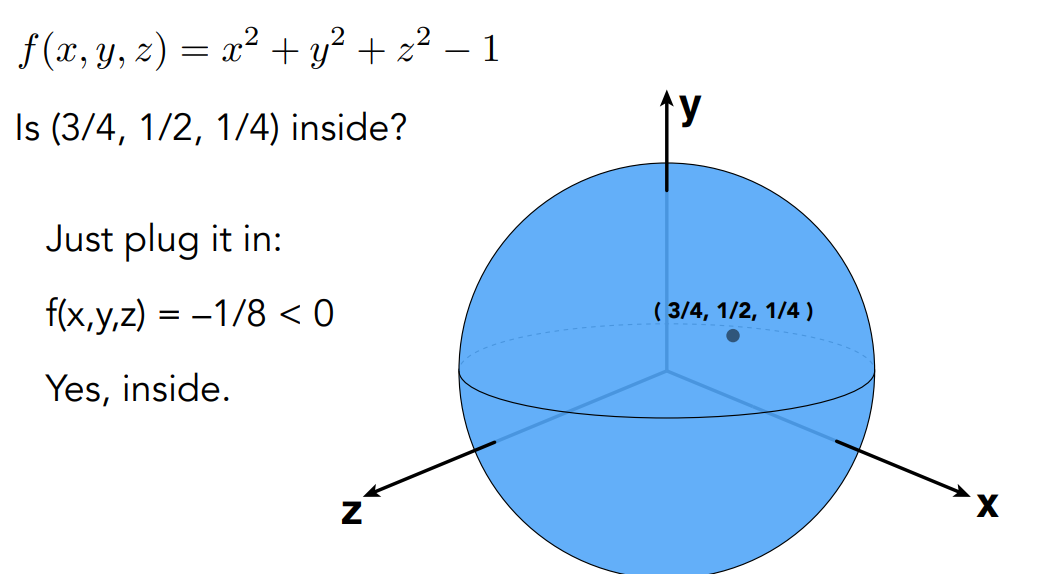
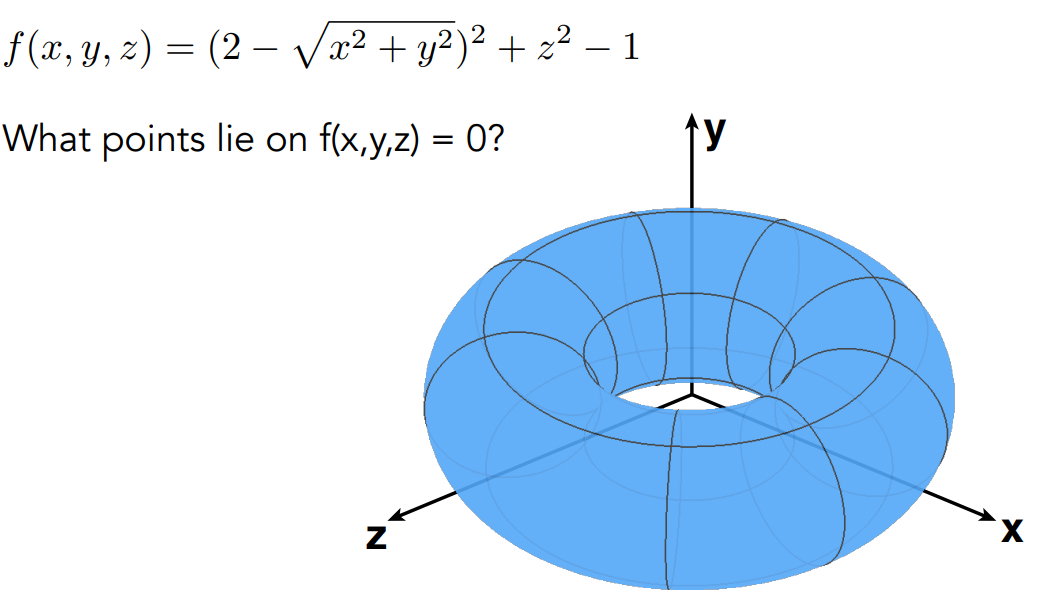
一般的表示 f(x,y,z)=0

隐式的表示优缺点：方便判断点在不在面上,inside/outside is easy（点面关系），但不容易看出面长什么样 simpling is hard（找出面的所有点）。

explicit geometry 直接给坐标或者映射得到坐标

与隐式对应的，显式的表达指把所有点直接的给出来，直接给出来空间坐标位置。

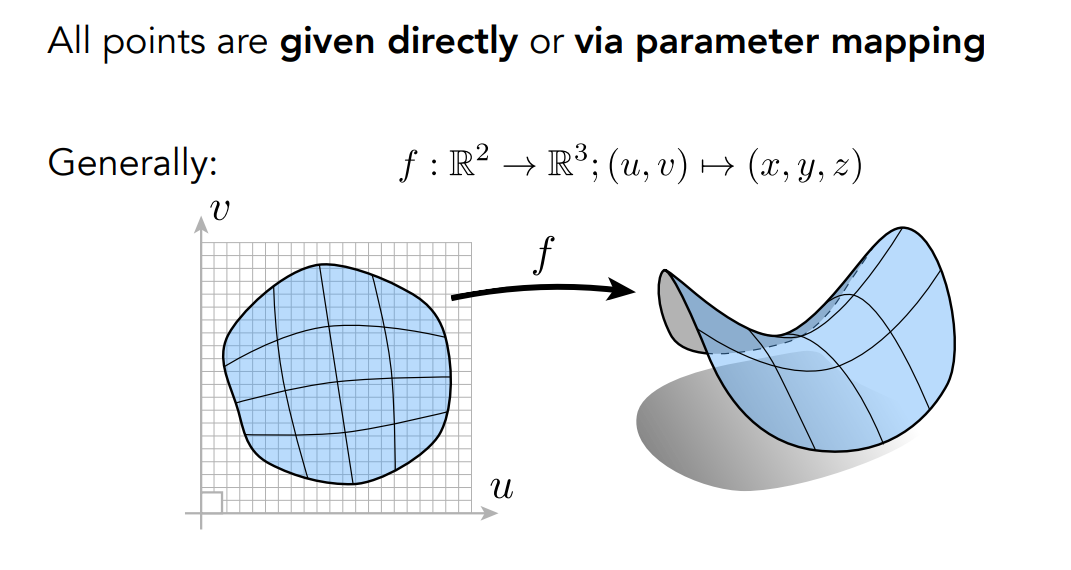
另一种显式的方法通过参数映射的方法定义的表面。
已经知道uv坐标的所有点以及参数映射函数F，将uv所有的点通过映射走一遍便可以得到所有点的空间坐标。

显式表面优缺点：点面关系判断变难，但是能直接得到坐标方便看(simpling is easy)

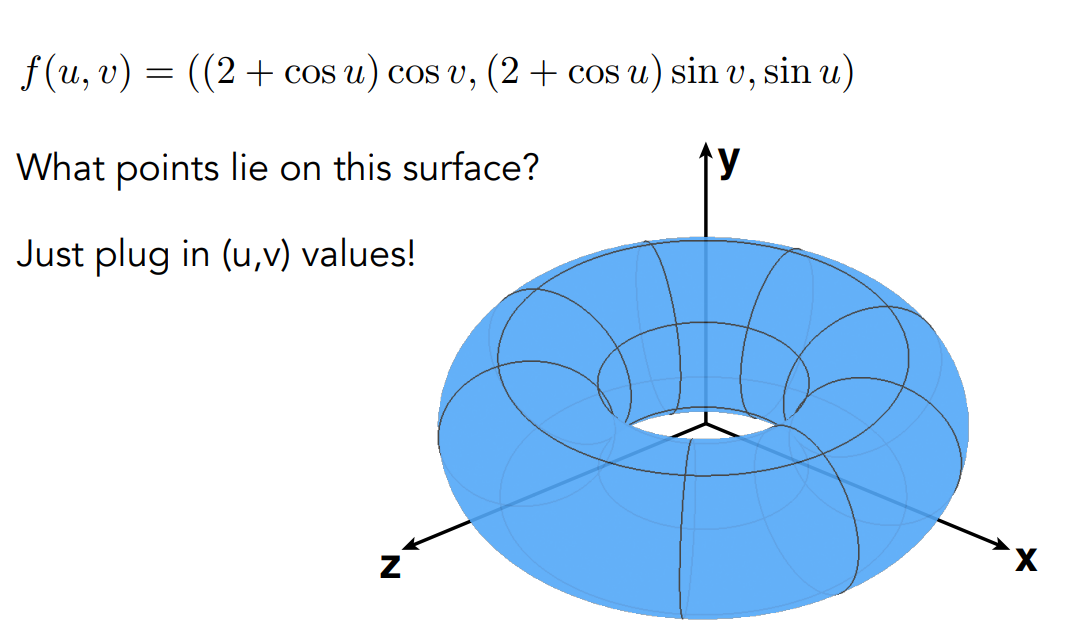
两种方法各有优缺点 适用于不同情况下。

另外的一些隐式几何表示

Algebraic surfaces

直接数学公式表示、但不直观。

Constructive Solid Geometry

定义基本几何的基本运算来表示新的几何

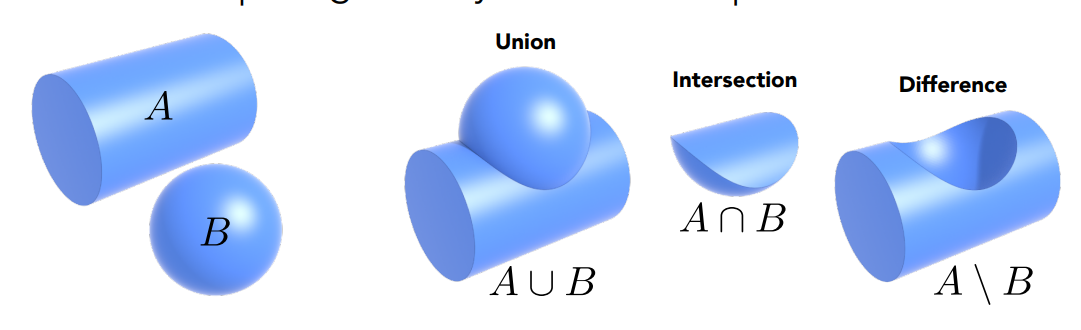
Distance Functions

距离函数(任何点到关心的地方的最近位置)定义几何进而表示几何的平滑过度（距离函数blend起来）

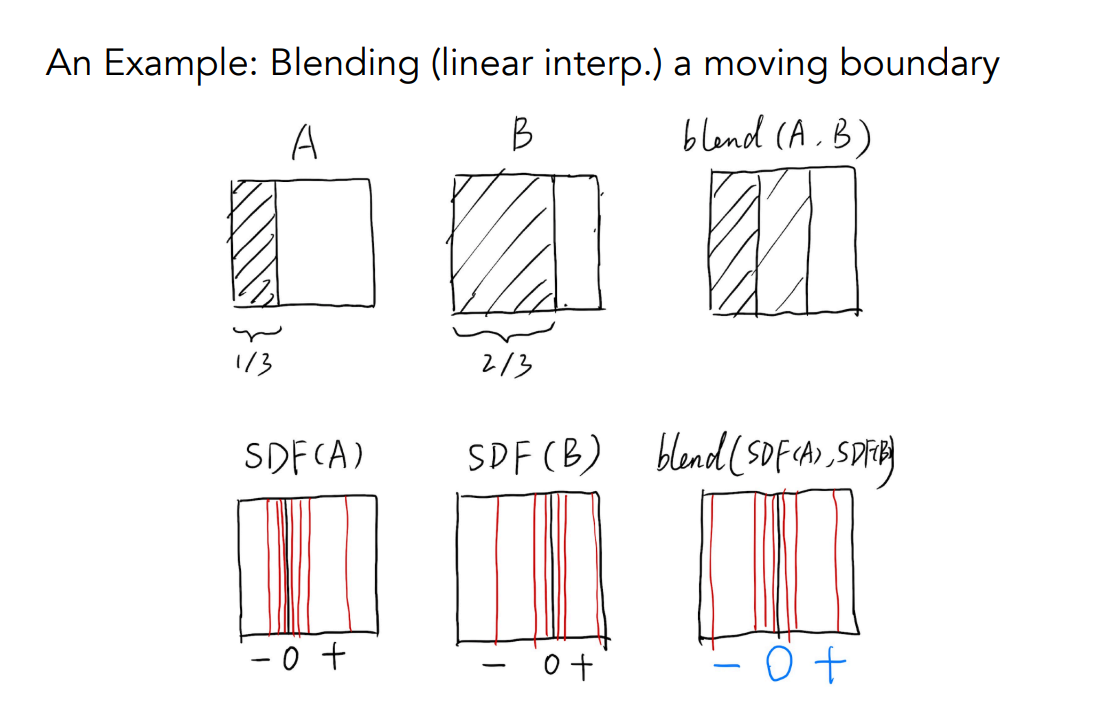
Level set methods

本质上也是距离函数，函数为0的地方代表着表面边界

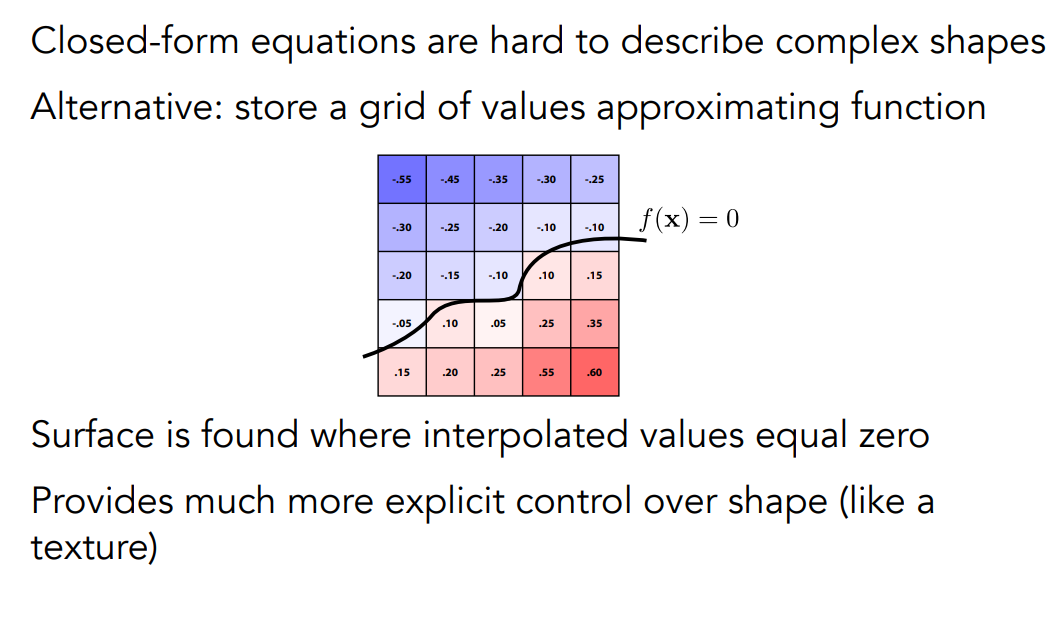
距离函数的不同形式表示，双线性插值找最终函数值为0的地方

水平集也可以定义在三维空间中

Fractals

分形、自相似表示.

隐式函数通常表示出来容易，一个公式描述一个形状，方便存储，支持查询，隐函数表示的隐式表面容易做光线求交。

问题：复杂形状难以描述--对应显式的表示。

另外的一些显式几何表示

point cloud

不考虑物体是一个表面，考虑表面上的一堆点，点足够密就看不到之间的缝隙-即成了一个面，也就是三维坐标系统中的一组向量的集合。

• 理论上能够表示任何的几何
• 三维空间扫描得到输出就是点云
• 较稀疏时便难看出图形

Polygon Mesh(多边形网格)

• 最常用的一种方法，将一些几何图形不断用三角形或者四边形去逼近近似，大部分API都是用这种方法去绘制一些基本的图形。复杂的导入obj格式文件。

• obj 文件格式

obj文件里面定义了几何图形的各个顶点位置、法线位置、纹理坐标位置、以及顶点的连接关系(为了形成Polygon mesh近似几何表面)

f 5/1/1 1/2/1 4/3/1:表示将第五个点、第四个点和第一个点连起来形成三角形，三角形的三个顶点对应的纹理坐标时第一个 第二个和第三个 用第一个法线作为方向

• 内容来源：
  • games 101