初探莫队
2019年的某月某天某神仙讲了莫队,但是我一直咕咕咕到了2020年
什么是莫队
莫队是一种优雅的暴力,也是用来完成区间询问的。普通莫队复杂度\(O(n \sqrt n)\)。一种十分优美的离线做法
前置芝士
0.拥有脑子
1.\(STL\)中\(sort\)的\(cmp\)
2.看/写超长的三目运算符的耐心
3.分块的思想
当然了如果不会这些也没有关系,下面还会再讲的
正片开始
先来一道卡了莫队的莫队模板题
HH的项链


最最暴力的做法:显然我们可以对每个询问暴力跑一次,但显然\(O(n^2)\)跑不起。
在上面的暴力中,我们浪费了大量之前遍历过的区间的信息,现在考虑利用起这些信息。我们可以设置两个指针\(l,r\)表示当前所处的区间左端点和右端点。初始化\(l=1,r=0\)。(为了避免某些神奇的\(RE\))如果\(l,r\)不与询问区间的端点重合,就不断的跳\(l,r\)来更新答案。如果\(l\)在左端点右边,就不断向左跳,同时将\(l\)跳到的数统计进答案中,直到与左端点重合。如果\(l\)在左端点左边,就不断往右跳,同时将曾经待过的点从答案中删掉。对于这个题来说,可以用\(cnt[x]\)表示\(x\)这个数出现的次数,如果某次增加时,\(cnt[x]==0\),\(ans\)就\(+1\),如果某次删除时发现删完后\(cnt[x]==0\),\(ans\)就\(-1\)。
我们发现上面这个优化对于这种图来说效率极高:

其中\(x_i\)表示第\(i\)次询问对应的区间
但是对于这种数据来说就凉了
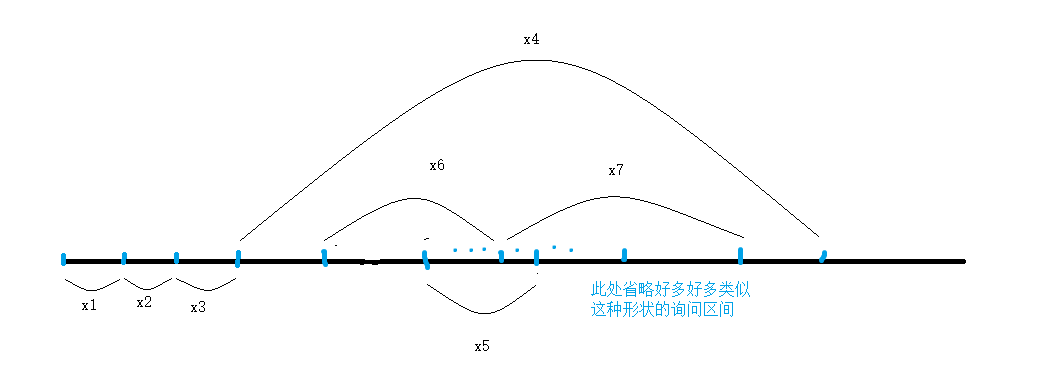
上面的优化方式在\(x_4\)里面不断得左右来回跳,导致浪费了大量的时间。
所以我们不妨把询问的区间进行排序。这样做就必须离线了。怎么排序呢?按照左端点单调递增?显然右端点无序会让这个优化只增加\(O(nlogn)\)的排序复杂度。这时候,就要用到分块思想了。
我们把整个序列分成\(\sqrt n\)个块,按照\(l\)所在的块升序排列为第一关键字,\(r\)升序排列为第二关键字排序。感觉好像没有什么用诶?但确实是个极大的优化至于为什么我也不知道
代码如下:
struct Q{
int l,r,id,nub;//nub表示左端点在哪个块里
}qry[200009];
bool cmp(Q a,Q b)
{
if(a.nub!=b.nub) return a.nub<b.nub;
return a.r<b.r;
}
当然卡常一点也可以写成这样:
bool cmp(Q a,Q b)
{
return (a.nub^b.nub)?a.nub<b.nub:a.r<b.r;
}
过莫队板子的必备技能是卡常
这样基本的莫队就撒花完结了。
因为这道板子题卡了莫队,所以请走数据弱化版D_QUERY
板子题代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline ll read()
{
char ch=getchar();
ll x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-') f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,q,a[30009],ans[200009],cnt[1000009],all;
struct Q{
int l,r,nub,id;
}qry[200009];
bool cmp(Q a,Q b)
{
if(a.nub!=b.nub) return a.nub<b.nub;
return a.r<b.r; //由于这题不卡常所以就没有卡
}
void add(int k)
{
if(!cnt[a[k]]) all++;
cnt[a[k]]++;
}
void del(int k)
{
cnt[a[k]]--;
if(!cnt[a[k]]) all--;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
q=read();
int sn=sqrt(n);
for(int i=1;i<=q;i++)
{
qry[i].id=i;qry[i].l=read();qry[i].r=read();
qry[i].nub=qry[i].l/sn+1;
if(qry[i].l%sn==0) qry[i].nub--;
}
sort(qry+1,qry+1+q,cmp);
int l=1,r=0;
for(int i=1;i<=q;i++)
{
while(r<qry[i].r) add(++r);
while(r>qry[i].r) del(r--);
while(l<qry[i].l) del(l++);
while(l>qry[i].l) add(--l);
ans[qry[i].id]=all;
}
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
}
莫队的玄学优化
奇偶性排序
虽然上面的排序方法优化很大,但是能不能更快一点以便卡过毒瘤题呢?
方法当然是有的辣。
我们先来康康按照上面的排序方法会排出来个啥
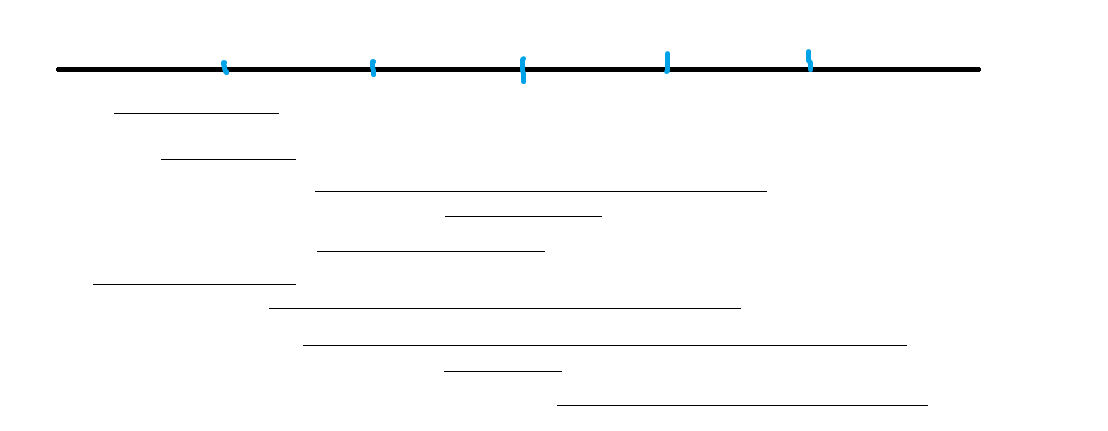
这是一堆询问区间以及并不优美的块的分界线
排序后:
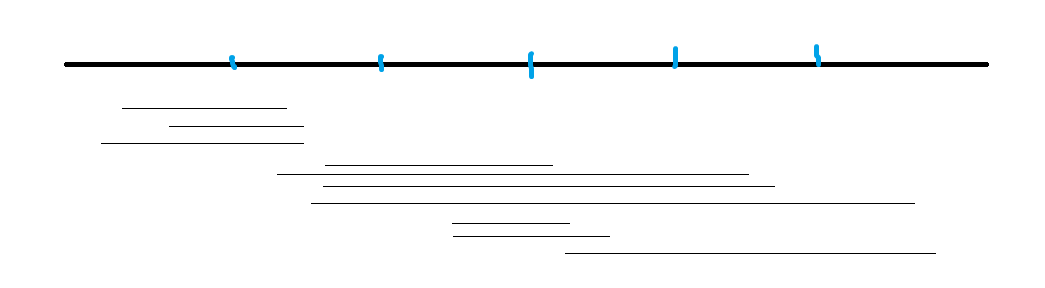
这样左端点跳动幅度不大,右端点在同一个块内也是递增的。但是当\(r\)从一个块跳到下一个块的时候发现有时候会倒退回来好多,然后又要重新向右跳。是不是有点浪费?所以奇偶性排序就是在奇数块内右端点按升序排序,偶数块内右端点按降序排序,这样右端点在往回跳的时候就能顺带跳完偶数块的询问。理论上能快一半
上面的按照奇偶性排序:
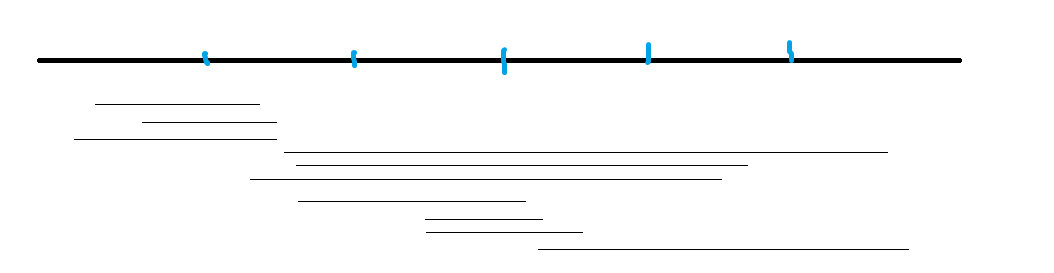
手动模拟\(r\)的跳跃发现真的优化了不少
代码:
bool cmp(Q a,Q b)
{
return (a.nub^b.nub)?(a.nub<b.nub):((a.nub%2)?a.r<b.r:a.r>b.r);
}
乱七八糟系列
\(pragma\ GCC\ optimize(2),pragma\ GCC\ optimize (3),register\),快读快输,\(inline\),把\(for\)里的\(i++\)换成\(++i\),用三目运算符代替blabla(待会卡带修莫队板子要用)
带修莫队
现在毒瘤出题人要求修改,怎么办呢?
就像这道题:数颜色


在很久很久以前,这道题是可以拿树套树卡过的你甚至只用去搞搞set,但是现在拿带修莫队都要吸氧了\(QAQ\)
好了我们回到正题。
我们只需要在原来的莫队的基础上再加一维时间轴。将询问和修改分开存储。如果这次询问的时间在当前时间之后,就不断修改,直到时间相同。如果询问时间在当前时间之前,就再改回去,我们可以用\(swap\)做到,从而不用再开变量维护原来的值。
当然了,排序方式也有变化。这次我们按照\(l\)所在的块为第一关键字,\(r\)所在的块为第二关键字,时间为第三关键字进行排序。同时,奇偶性排序也不再适用。
排序:
bool cmp(Q a,Q b)
{
return (bl[a.l]^bl[b.l])?bl[a.l]<bl[b.l]:((bl[a.r]^bl[b.r])?bl[a.r]<bl[b.r]:a.ti<b.ti);
}
注意块的大小会对复杂度有着极大的影响。据大佬证明当块的大小为\(n^{\frac{3}{4}}\)时,复杂度最优。
由于这个题窝太菜了,不拿\(O_2\)实在是卡不过去,所以只好放上一份加\(O_2\)的代码了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,k,q,a[133339],bl[133339],ans[133339],cnt[1000009];
int all;
struct Q{
int l,r,ti,id;
}qry[133339];
struct M{
int p;
int col;
}mdi[133339];
bool cmp(Q a,Q b)
{
return (bl[a.l]^bl[b.l])?bl[a.l]<bl[b.l]:((bl[a.r]^bl[b.r])?bl[a.r]<bl[b.r]:a.ti<b.ti);
}
inline void add(int k)
{
if(!cnt[a[k]]) all++;
cnt[a[k]]++;
}
inline void del(int k)
{
cnt[a[k]]--;
if(!cnt[a[k]]) all--;
}
inline void modi(int i,int ti)
{
if(mdi[ti].p>=qry[i].l&&mdi[ti].p<=qry[i].r)
{
int x=--cnt[a[mdi[ti].p]];
int y=++cnt[mdi[ti].col];
if(!x) all--;
if(y==1) all++;
}
swap(a[mdi[ti].p],mdi[ti].col);
}
int main()
{
n=read();q=read();
for(int i=1;i<=n;i++)
a[i]=read();
int qc=0,mc=0;
for(int i=1;i<=q;i++)
{
char k=getchar();
while(k!='Q'&&k!='R') k=getchar();
if(k=='Q')
{
qry[++qc].l=read();qry[qc].r=read();
qry[qc].ti=mc;qry[qc].id=qc;
}
if(k=='R')
{
mdi[++mc].p=read();mdi[mc].col=read();
}
}
int sn=pow(n,3.0/4.0);
for(int i=1;i<=n;i++)
{
bl[i]=(i-1)/sn+1;
}
sort(qry+1,qry+1+qc,cmp);
int now=0,l=1,r=0;
for(int i=1;i<=qc;i++)
{
while(r<qry[i].r) add(++r);
while(r>qry[i].r) del(r--);
while(l<qry[i].l) del(l++);
while(l>qry[i].l) add(--l);
while(now<qry[i].ti) modi(i,++now);//带修莫队只是多了这两个修改操作
while(now>qry[i].ti) modi(i,now--);
ans[qry[i].id]=all;
}
for(int i=1;i<=qc;i++)
printf("%d\n",ans[i]);
}
莫队可以处理区间上的东西,而\(dfs\)序这种东西可以把树转化成区间,那么莫队可不可以解决树上的问题呢?
树上莫队
我们以这道题SP10707 COT2 - Count on a tree II为例,来看看树上莫队。

样例:

把样例画出来:

显然我们需要\(dfs\)序来把这棵树变成一个序列。
普通的\(dfs\)序: 1 2 3 5 6 7 4 8
2到5的路径:2 1 3 5
咦可以乱搞的区间去哪里了???
显然,普通的\(dfs\)序不能用莫队进行乱搞,所以,我们需要一种特殊的\(dfs\)序。
欧拉序
欧拉序是一种特殊的\(dfs\)序,当遍历到一个点时,将它加入\(dfs\)序中,再遍历它的子树。当它的子树遍历完时再将它加入到\(dfs\)序中。
煮个栗子:

这个图中,欧拉序是 1 2 2 3 5 5 6 6 7 7 3 4 8 8 4 1
可以看出每个点都会出现两遍,而且这两遍中间的所有点都是它的子树里的节点。这样有什么优点呢?
我们再来找找2到5的路径(2 1 3 5):
1呢?1被吃了。1作为2,5的\(lca\),在欧拉序中1在2的前面所以1被吃了
我们先存一下这个即将成为历史遗留问题的问题,看一下具有祖孙关系的节点之间的路径怎么求。
炒个栗子:
1到6的路径:1 3 6
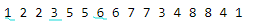
emmm也许我们又多了一个历史遗留问题
so我们应该怎么找路径对应的区间解决历史遗留问题呢?
我们可以记录每个点\(i\)在欧拉序中第一次出现的位置\(first[i]\)(以下简写为\(fst[i]\))和最后一次出现的位置\(last[i]\)(以下简写为\(lst[i]\))。我们现在要找\(u\)到\(v\)的路径对应的区间(这里假设\(fst[u]<fst[v]\),不满足就\(swap\)),如果\(lca(u,v)==u\),就是\([fst[u],fst[v]]\)这段区间的答案,否则,是\([lst[u],fst[v]]\)这段区间的答案。\(why?\)打表可得因为\(lca\)在\(u\)和\(v\)的上面,所以从\(u\)走到\(v\)一定是回溯完\(u\)才能到\(v\),所以是区间左端点是\(lst[u]\)而不是\(fst[u]\)。
我们注意到按照上面的找区间方法并没有解决历史遗留问题1中的处理\(lca\),同时也有可能会在确定的区间中发现某些节点出现了两次。所以我们应该特殊处理一下。第奇数次走到某个节点,就进行类似\(add\)的操作,而第偶数次遍历到某个节点就进行类似\(del\)的操作,可以消除区间中出现两次的点(实际上在树上并没有经过的点)的影响。对于\(lca\),我们单独进行上面所说的操作,统计完答案后再操作一次来消除这次操作对后面的影响。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=214748364;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-') f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,m,a[40009],cnt,head[40009],fst[40009],lst[40009];
int qwq[80009],q,tot,dep[40009],f[40009][21],bl[80009];
int b[40009],w,ans[100009],all,num[40009];
bool vis[80009];
struct E{
int to,nxt;
}ed[80009];
struct Q{
int l,r,id,lca;
}qry[100009];
void add(int fr,int to)//这个是存边的add,不是维护答案的add
{
ed[++cnt].to=to;
ed[cnt].nxt=head[fr];
head[fr]=cnt;
}
void dfs(int now,int fa)
{
dep[now]=dep[fa]+1;
qwq[++tot]=now;fst[now]=tot;
f[now][0]=fa;
for(int e=head[now];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(v==fa) continue;
dfs(v,now);
}
qwq[++tot]=now;lst[now]=tot;
}
int Lca(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
for(int i=20;i>=0;i--)
if(dep[f[u][i]]>=dep[v]) u=f[u][i];
if(u==v) return u;
for(int i=20;i>=0;i--)
{
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
}
return f[u][0];
}
//以上是倍增搞lca
int fd(int k)
{
int l=1,r=w;
while(l<=r)
{
int mid=(l+r)>>1;
if(b[mid]==k) return mid;
if(b[mid]>k) r=mid-1;
else l=mid+1;
}
while(b[l]>k) l--;
return l;
}
//由于数据过大,进行离散化
bool cmp(Q a,Q b)
{
return (bl[a.l]^bl[b.l])?(bl[a.l]<bl[b.l]):((bl[a.l]%2)?a.r<b.r:(a.r>b.r));
}
void deal(int k)//对区间进行的操作
{
(vis[k])? all-=!(--num[a[k]]) :all+= !num[a[k]]++;
vis[k]^=1;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=a[i];
for(int i=1;i<=n-1;i++)
{
int fr=read(),to=read();
add(fr,to);add(to,fr);
}
sort(b+1,b+1+n);
w=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++)
a[i]=fd(a[i]);
dfs(1,0);
for(int j=1;j<=20;j++)
for(int i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
for(int i=1;i<=m;i++)
{
qry[i].id=i;int u=read(),v=read();
if(fst[u]>fst[v]) swap(u,v);
int lca=Lca(u,v);
if(lca==u) qry[i].l=fst[u],qry[i].r=fst[v],qry[i].lca=0;
else qry[i].l=lst[u],qry[i].r=fst[v],qry[i].lca=lca;
}
int sn=sqrt(2*n);
for(int i=1;i<=2*n;i++)
bl[i]=(i-1)/sn;
sort(qry+1,qry+1+m,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++)
{
while(r<qry[i].r) deal(qwq[++r]);
while(r>qry[i].r) deal(qwq[r--]);
while(l<qry[i].l) deal(qwq[l++]);
while(l>qry[i].l) deal(qwq[--l]);
if(qry[i].lca) deal(qry[i].lca);
ans[qry[i].id]=all;
if(qry[i].lca) deal(qry[i].lca);
}
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号