洛谷 P6599 「EZEC-2」异或 题解

题目链接；

由于符号等缘故，题面在此不再粘贴，想看题面的可以点击上方链接或windows左右分屏观看；

---

1.题外话

看到∑，就恶心；

看到黄题，就想切；

总之，心情很复杂，硬着头皮看下去，发现没这么难

2.解题意

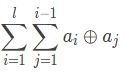
外层循环，从1~i；

内层循环，从1~j；

从第二层循环考虑，易知对于每一个ai，都会和位于其之前的aj进行一次异或并且加和。并且当i增大后，位于当前这个ai后面的a元素也会与其进行异或并累加；

也就是说，我们可以这样理解：每一个ai都与序列l中剩下的a进行了一次异或并且累加。

这是对于一个ai；将外层循环考虑在内，我们就知道：题目让求的就是所有的元素与其他任意一个元素的异或之和。（类似于两两握手那种问题。只不过是把握手换成了异或）。

3.找思路

由数据得，a最大为10^12.因为是异或，那么二进制表示下各个位数之间互不干扰。并且题目只是给了n，要使∑值最大，很容易便想到每一个a都需要达到位数上限n。既然位数相同，题目又没有给你具体每一个a的数值，我们便可以一位一位考虑，每一位取到和的最大值，再*2^k进行累加即可。

求答案的方法已经基本成型了，剩下的就是确定每一位异或和最大的情况。

对一位进行考虑：

两两异或，其中一个为1，另一个为0，则答案为1。

我们设有x个数为0。

对于每一个为1的数，都可以和所有为0的数异或得1，对答案的贡献就是x；

总个数为l，则剩下的大小为1的数有l-x个，一个就可以为答案增加x，l-x个就可以为答案增加x*（l-x）。很明显，当x取中间值l/2时上式取值最大.（具体为什么参考“和同近积大”原理或者二次函数求极值即可）

于是，我们求得了每一位对答案最大的贡献，接着把每一位对答案的贡献累加起来，就是题目所求答案。

4.代码实现

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define ll long long
#define re register
#define modd 1000000007
using namespace std;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int t;
long long n,l,ans;
int main()
{
    t=read();
    while(t--)
    {
        ans=0;
        scanf("%lld%lld",&n,&l);
        long long mid=l>>1;//求最大值所用
        if(n==1)//特判、因没有而WA掉。简单思考一下就知道了
        {
            printf("0\n");
            continue;
        }
        long long big=1ll<<40;//10^12到不了40位
        while(big)
        {
            big>>=1;
            if(n<big)continue;//如果没到n的最大位，就位数--
            ans+=big*mid*(l-mid);//累加答案
            ans%=modd;//不取模见祖宗
        }
        printf("%lld\n",ans);
    }
    return 0;
}

完结撒花。