P1058 立体图题解
小渊是个聪明的孩子,他经常会给周围的小朋友们将写自己认为有趣的内容。最近,他准备给小朋友们讲解立体图,请你帮他画出立体图。
小渊有一块面积为m \times nm×n的矩形区域,上面有m \times nm×n个边长为11的格子,每个格子上堆了一些同样大小的积木(积木的长宽高都是11),小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式,并且不会做任何翻转旋转,只会严格以这一种形式摆放:
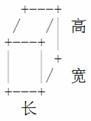
每个顶点用11个加号’++’表示,长用33个”-−”表示,宽用11个”/”,高用两个”|”表示。字符’++’,”-−”,”/”,”|”的ASCIIASCII码分别为4343,4545,4747,124124。字符’.’(ASCIIASCII码4646)需要作为背景输出,即立体图里的空白部分需要用’.’来代替。立体图的画法如下面的规则:
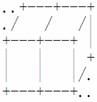
若两块积木左右相邻,图示为:
若两块积木上下相邻,图示为:
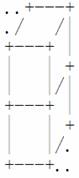
若两块积木前后相邻,图示为:

立体图中,定义位于第(m,1(m,1)的格子(即第mm行第11列的格子)上面自底向上的第一块积木(即最下面的一块积木)的左下角顶点为整张图最左下角的点。
输入输出格式
输入格式:
第一行有用空格隔开的22个整数mm和nn,表示有m \times nm×n个格子(1 \le m,n \le 50)(1≤m,n≤50)。
接下来的mm行,是一个m \times nm×n的矩阵,每行有nn个用空格隔开的整数,其中第ii行第jj列上的整数表示第ii行第jj列的个子上摞有多少个积木(1 \le1≤每个格子上的积木数\le 100≤100)。
输出格式:
输出包含题目要求的立体图,是一个KK行LL列的字符串矩阵,其中KK和LL表示最少需要KK行LL列才能按规定输出立体图。
题解部分:
题都读不懂?
其实就是给你长宽,给你三视图(主,侧,俯)中的俯视图,然后让你画它的三维立体图。
本题思路源泉:P1003 铺地毯
也就是一个覆盖的思想。
众所周知,三维图要满足遮挡关系,也就是前面的遮挡后面的,右面的遮挡左边的。
那么我们用透视关系来覆盖。
那么我们枚举每一个二维方块位置,然后在每一个二维平面位置上一个一个网上摞方块就可以了。
具体的,因为每一个方块为一个面积,那么我们只能抽象成一个点来进行枚举
我们把一个方块抽象为左上角的点,于是枚举左上角的点再进行覆盖。
这个题就这样了。。
代码:
#include<cstdio> #include<iostream> using namespace std; int read(){ int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') { ans=(ans<<1)+(ans<<3)+(ch^48); ch=getchar(); } return last=='-'?-ans:ans; } char c[1001][1001],c1[10][10]={//倒着存储 "+---+", "| |/", "| | +", "+---+ |", " / /|", " +---+", };//6行7列 的方块 int n,m,jz[51][51],maxh=-1,maxl=-1,zbx,zby; inline void fg(int zbx,int zby)//覆盖操作 { for(int i=0;i<=4;i++)c[zbx][zby+i]=c1[0][i]; for(int i=0;i<=5;i++)c[zbx+1][zby+i]=c1[1][i]; for(int i=0;i<=6;i++)c[zbx+2][zby+i]=c1[2][i]; for(int i=0;i<=6;i++)c[zbx+3][zby+i]=c1[3][i]; for(int i=1;i<=6;i++)c[zbx+4][zby+i]=c1[4][i]; for(int i=2;i<=6;i++)c[zbx+5][zby+i]=c1[5][i]; } int main(){ // freopen("drawing.in","r",stdin); // freopen("drawing.out","w",stdout); m=read();n=read(); for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { jz[i][j]=read(); } } for(int i=1;i<=m;i++)//从输入的矩阵的左上角开始,满足先后,先左 for(int j=1;j<=n;j++) { zbx=(m-i)*2+1;zby=(m-i)*2+1+4*(j-1); for(int k=1;k<=jz[i][j];k++,zbx+=3) { fg(zbx,zby); } if(zbx+2>maxh)maxh=zbx+2;//我不知道为什么 if(zby+6>maxl)maxl=zby+6; } for(int i=maxh;i>=1;i--) { for(int j=1;j<=maxl;j++) { if(c[i][j]=='\0') printf("."); else printf("%c",c[i][j]); } printf("\n"); } return 0; }
完结


 浙公网安备 33010602011771号
浙公网安备 33010602011771号