卡特兰数以及应用&&P1044 栈 题解

卡特兰数：

卡特兰数以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名 字来命名。

它的表达（递推式子）:                           

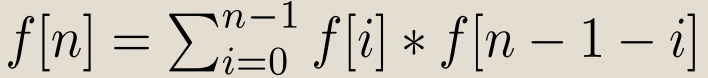其中f[i]表示卡特兰数第i项，f[0]=f[1]=1;

于是乎，并没有看出这个有什么鬼用。，。

也就是：——度娘，这个版本比较清楚易懂。

这个东西有什么用？

1，出栈序列问题。

栈是一个先进先出的结构，对于一列数，问你它一共有多少种出栈序列（方案数）？

这个问题完美契合卡特兰数。也就是洛谷P1044 栈。

对于当前要求的n，考虑第n个元素出栈，那么这个元素的大小是不定的，如果把序列从小到大排列的话，一共有n种，对于其中一种now=i，有n-now个比它大的，有now-1个比它小的，那么把f[now-1]和f[n-now]乘起来就是当前一种情况的方案数。一共有n种，那么就有n种情况，把他们加起来，就是这个东西：没错就是卡特兰数。

代码：

#include<cstdio>
#include<iostream>
using namespace std;
int f[20],n;
int main(){
    scanf("%d",&n);
    f[0]=f[1]=1;
    for(int i=2;i<=n;i++)//递推求卡特兰数
    {
        for(int j=1;j<=i;j++)//枚举n种情况
        {
            f[i]+=f[i-j]*f[j-1];//累加求当前卡特兰数
        }
    }
    printf("%d",f[n]);//输出题目要求的那项。
    return 0;
} 

还有这些。。。。

都是卡特兰数典型题目。

初步认知，还望各位赐教Orz

完结