2021-OO-UNIT3-总结

BUAA-OO-JML-blog

一、设计策略

  • 由于在下文中涉及到性能问题的分析，因此在本部分将不会重点分析所采用设计策略的优劣，而是依据三次作业时间先后的迭代和改动对具体策略做出介绍；同时，由于异常类的设计较为统一而复杂程度低，因此将其独立地简单介绍。

    异常类

    • 在My***Exception类中设置static类型的变量，如该代码所示：

      private static int countTotal = 0;
      private static HashMap<Integer,Integer> idToCount = new HashMap<>();

      当该异常被抛出时，维护上述的静态类型变量，并将其按照题目要求格式打印。可以看出，异常类的实现策略较为简单。

    第一次作业

    • 在第一次作业中，仅有Person与Network两个待具体实现的接口，且方法较为简单，因此对于大部分属性和方法，采取了“翻译规格”的策略实现（即：将JML规格中的语句按照符合Java语法的方式进行翻译），额外设计的策略并不多。值得注意的是isCircle()与queryBlockSum()两个方法，对其设计了复杂度较低的策略。

      1. isCircle(int id1, int id2)

        • 为了避免在该方法中以复杂度较高的形式对人群遍历（同时，遍历后的结果无法保存，每次查询时均需要重新遍历），笔者在程序中维护了一个具有并查集思想的数据结构。其具体实现简述如下：

          首先，在每个人身上（即：在MyPerson类中）维护一个变量：Ancestor，值为该人员的祖先ID。当每次新添加人时，该人员的祖先都是它自己。

          其次，在MyNetwork中维护数据结构如下：

          private HashMap<Integer,ArrayList<MyPerson>> idToChild;

          其Key值代表了祖先的ID，而Value值则存储了该祖先所有孩子（只要人员的Ancestor值与该祖先ID值相等，其便为该祖先的孩子）。

          容易想到对于上述数据结构的维护。当新增关系时，找到新增关系的两个人的祖先。若二者的祖先为同一人，则不需做出改变；若二者的祖先ID不同，则从两个祖先中选出一个祖先A（一般选取孩子数较多的），将另一祖先B的所有孩子（也包括B本身）的祖先重新设置为A（改变Ancestor值，并维护上述HashMap）。

          经过上述维护，当我们调用isCirCle(int id1, int id2)方法时，仅仅需要判断二者的祖先是否相等：

          return ((MyPerson) getPerson(id1)).getAncestor() == ((MyPerson) getPerson(id2)).getAncestor();

      2. queryBlockSum()

        • 若依据“翻译规格”的策略实现该方法，则复杂程度较高。因此，笔者选择了抓住BlockSum块的本质（即阻塞块），按照以下逻辑进行实现。具体策略如下：

          首先，在MyNetwork中设置一个成员属性：blockSum，初始值为0。

          对于该属性的具体维护，当新增人时，blockSum++；当新增关系时，若二者祖先不同，则blockSum--。

          经验证，该策略所计算结果正确。

    第二次作业

    • 在第二次作业中，与上一次作业相同的方法均未改变实现策略。由于新增了Group接口和Message接口需要实现，因此新添的方法也主要与Group、Message相关。大部分方法仍然采用了“翻译规格”的实现策略，依照规格完成；与规格逻辑有所不同的实现策略主要为getValueSum()，getAgeMean()，getAgeVar()（均为Group接口所需实现的方法）。

      1. getValueSum()

        在MyGroup类中维护了变量：value，初始值为0。

        当调用addValue()方法时，增加value值（addValue()方法可能在其他类新增关系时被调用）；

        当往group中新增人时，遍历该组原来包含的人，若某人与该新增人相识，则value值增加（增加具体数值此处不给出）；

        当往group中删人时，遍历该组其他人，若某人与所删人相识，则value值减少（减少具体数值此处不给出）。

      2. getAgeMean()

        采用缓存的思想，在MyGroup类中维护属性：ageSum，即所有人的年龄总和，其初始值为0。

        对于该变量的维护，仅需在新增人和删人时体现，具体策略符合日常逻辑。

      3. getAgeVar()

        对于方差的计算，同样可以采用缓存的策略。上文中已经提及ageSum属性的维护，再维护一个变量：sumTwo，代表所有人的年龄平方总和（对于该变量的维护与ageSum类似）。当计算方差时，能通过以下公式计算：

        return (sumTwo - 2 * sum * mean + n * mean * mean) / n;

    第三次作业

    • 第三次作业中，大部分新增方法仍然采用“翻译规格”的策略实现，值得一提的是：sendIndirectMessage(int id)方法。

      1. sendIndirectMessage(int id)

        在该方法中，重点是最短路径的查找。为了实现最短路径的确定，采用Dijkstra算法，结合缓存思想，该策略能够有效提高程序效率。

        首先，在MyPerson中维护属性：flag（标志位）以及一个HashMap：

        private HashMap<Integer,Integer> ways;

        其中，flag标志着该人与他的所有熟人的最短路径是否已经找到；若flag为true，则该HashMap ways缓存着熟人ID与对应的最短路径距离。

        当在该方法寻求两个人的最短距离时，首先判断两人中是否有人的flag为true：若有，则仅需返回该人的ways中已经缓存起来的最短路径距离；若无，则按照Dijkstra算法寻找。

        关于Dijkstra算法以及其具体实现，在本文中并不具体阐述。可以参照以下链接的文章及视频：

        在笔者程序中，采用了堆优化策略，显著提升了Dijkstra算法的效率。其参考文章如下：

        我们知道，Dijkstra算法能够得到某点到其他所有点的最短路径。对应到该方法中，即得到某人到达与他相识的所有人的最短距离。因此，每次成功执行该策略时，便将得到的最短路径结果缓存到该人的ways属性中（即上文介绍的HashMap），并将flag标志位置true。当新增关系时，可能有必要将flag重新置为false。

二、基于JML规格的测试方法及策略

  • 由于本单元与JML的密切相关，因此一个重要的测试方法即为：阅读JML规格。对于JML的阅读理解并不止步于代码编写的完成，在后续检验和测试的过程中仍然反复阅读，并与自己的代码进行对照，看是否存在出入。在第一次作业中，通过对于JML规格的静态阅读和对比，成功找到将messages.contains()（本意：对Message使用）错写为contains()（该方法为对Person使用）的bug。

  • 此外，编写测评机代码并对拍。测评机由Python编写而成，生成侧重点不同的测试数据，比较正确性并观察程序运行时间。例如，在第一次作业中高强度加人、加关系并高强度测试isCircle()及queryBlockSum()方法；在第三次作业中重点为加人、加关系并调用sendIndirectMessage()方法；每次独立对于异常进行测试......

三、容器选择和使用的经验

  • 本单元作业，主要使用了ArrayList、HashMap及PriorityQueue容器。

三次作业的容器演变

  • 在第一次作业、第二次作业中，出于“翻译规格”的策略思想，我大多使用ArrayList作为存储容器；然而经历了第二次作业的测试，我意识到了自己程序潜在的超时风险。因此，我主要用HashMap取代了ArrayList。举例对比如下：

    • 在JML规格中，对于Network的属性实现，有这样的语句：

      @ public instance model non_null Person[] people;

      在前两次作业中，我的实现方式如下：

      private ArrayList<Person> people;

      而在第三次作业中，我的实现方式如下，其中Key值代表人员ID：

      private HashMap<Integer,Person> people;

    • 在JML中，对于Person的属性实现，有这样的语句：

      @ public instance model non_null Person[] acquaintance;
@ public instance model non_null int[] value;

      在前两次作业中，我的实现方式如下：

      private ArrayList<Person> acquaintance;
private ArrayList<Integer> value;

      而在第三次作业中，我的实现方式如下：

      private HashMap<Person,Integer> acquaintanceToValue;

ArrayList与HashMap

  • 当我使用HashMap代替了ArrayList之后，程序的运行效率有显著提升。为何两个容器的效率会有这样的差异？ArrayList是一个维护元素特定顺序的数据结构，然而在该程序大多数地方并没有维持元素顺序的需求，因此使用ArrayList无法做到物尽其用。而在HashMap中搜索键相比于ArrayList快许多：查阅源码可知，HashMap使用特殊的值，即散列码（hash code），来取代对于键的缓慢搜索。

  • 更具体一点说，HashMap内部维护数据的方式为：数组链表+散列机制。定义一个数组，数组的每一个成员均为链表。在put一个元素时，根据key值的hash code，余上数组的容量，得到数组下标，将这个key-value对存储在该下标对应的链表内。在查询时，不需要盲目地线性遍历全部元素，只需要查找一条链表，提高了程序效率。

  • 具体可以参考网页文章：

勿自己造轮子

  • 在第三次作业的完成中，重要的一部分是：完成Dijkstra算法的实现。开始时，我陷入了固步自封的泥沼，试图自己造轮子完成算法，并认为自己的轮子并不慢。没想到，在测试对拍的过程中，发现自己的程序计算最短路径的效率极低，严重影响速度。因此，我和舍友交流，google查阅相关资料，才发现前人早已提供了Dijkstra算法的优质实现方式，同时Java也提供了效率较高的数据结构：PriorityQueue。在定义了排序之后，该数据结构能够将元素按一定的顺序进行排序。利用该数据结构，我成功地提高了程序效率。这再次警示着我，编写程序是学习的过程，要学会站在前人的肩膀上，不要做重复且低效的无用功。

四、性能问题,原因及避免策略

1.isCircle

  • 该方法查询两人是否连通，即要找到一条连通二者的熟人线。根据规格的描述，很容易采用BFS或DFS的方法进行暴力求解（事实上，我在开始时便是如此），这样的复杂度为O(n)，当n较大时容易导致性能较低。

  • 因此，我采用类似并查集的思想进行维护。与大多数人所使用的并查集不同的是，在我的程序中只有两层结构，即Ancestor与它的孩子们（也包括其本身），不会出现多层嵌套的结构。

  • 关于该类似并查集的数据结构的实现，在策略部分已经有所介绍。在此简单赘述：

    首先，在每个人身上（即：在MyPerson类中）维护一个变量：Ancestor，值为该人员的祖先ID。当每次新添加人时，该人员的祖先都是它自己。

    其次，在MyNetwork中维护数据结构如下：

    private HashMap<Integer,ArrayList<MyPerson>> idToChild;

    其Key值代表了祖先的ID，而Value值则存储了该祖先所有孩子（只要人员的Ancestor值与该祖先ID值相等，其便为该祖先的孩子）。

    容易想到对于上述数据结构的维护。当新增关系时，找到新增关系的两个人的祖先。若二者的祖先为同一人，则不需做出改变；若二者的祖先ID不同，则从两个祖先中选出一个祖先A（一般选取孩子数较多的），将另一祖先B的所有孩子（也包括B本身）的祖先重新设置为A（改变Ancestor值，并维护上述HashMap）。

    经过上述维护，当我们调用isCirCle(int id1, int id2)方法时，仅仅需要判断二者的祖先是否相等：

    return ((MyPerson) getPerson(id1)).getAncestor() == ((MyPerson) getPerson(id2)).getAncestor();

2.queryBlockSum

  • 该方法查询阻塞块数，若采取“翻译规格”的做法，有两层遍历。复杂度较高。

  • 因此，在实现并查集的同时顺便维护参数blockSum。加人时，需要增加blockSum大小；加关系时，判断二者祖先是否相同，若不同则减小blockSum大小。上述操作的复杂度均为O(1)。

3.sendIndirectMessage

  • 该方法需要查询最短路径。大多数人的策略均采用Dijkstra算法，因此重点在于采取良好的数据结构，以及合理的缓存机制。

  • 事实上，若采用朴素Dijkstra算法，则复杂度为O(n^2)，严重影响性能。而采用数据结构：PriorityQueue，令其进化为Dijkstra堆优化，有效地将复杂度降为O(n*log(e))。另外，将查询得到的点缓存（当然，可能在加关系过程中清除缓存数据），能在一些情况下使复杂度为O(1)。

4.getAgeMean

  • 该方法需要计算组中所有人的平均年龄。若未采用缓存机制，则复杂度为O(n)。该方法的重要性体现在于：不仅可能被反复频繁调用，同时在getAgeVar（即：计算年龄方差的方法）中也会被调用。因此，必须降低该方法的复杂度，避免超时。

  • 采取的方法是，在MyGroup类中维护属性：ageSum，即所有人的年龄总和，其初始值为0。对于该变量的维护，仅需在新增人时增加人的年龄值，删人时减去人的年龄值。需要计算平均值时，复杂度为O(1)。

5.getAgeVar

  • 若未缓存ageSum，也未缓存ageTwo（即：组中所有人年龄平方和），则该方法的复杂度为O(2n)，严重影响程序性能。

  • 因此，我们缓存并维护上述两个属性，通过数学公式来计算年龄的方差，有效降低复杂度。数学公式可表达为：

    return (sumTwo - 2 * sum * mean + n * mean * mean) / n;

6.getValueSum

  • 若依据“翻译规格”的策略完成该方法，则复杂度应为O(n^2)，严重影响程序性能。必须调整方法。

  • 因此，采用缓存的思想，在MyGroup中维护一个value值。对其的维护具体体现为：组增人、组删人、组中人添加关系时，均要对value值作一定修改。如此，getValueSum方法仅需查询value值，复杂度为O(1)。

五、梳理作业架构设计

  • 为了保持一定程度的简洁，在构建UML类图时省略了异常部分。

  • 由于关于策略部分的分析前面已经涉及大量，因此该部分也并不着重提及。

第一次作业

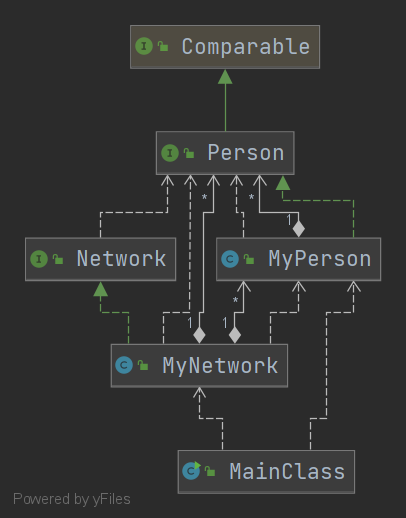
  • 第一次作业的架构如图所示，与JML规格所提供的结构无异，整体较为简单，故没有具体分析。

第二次作业

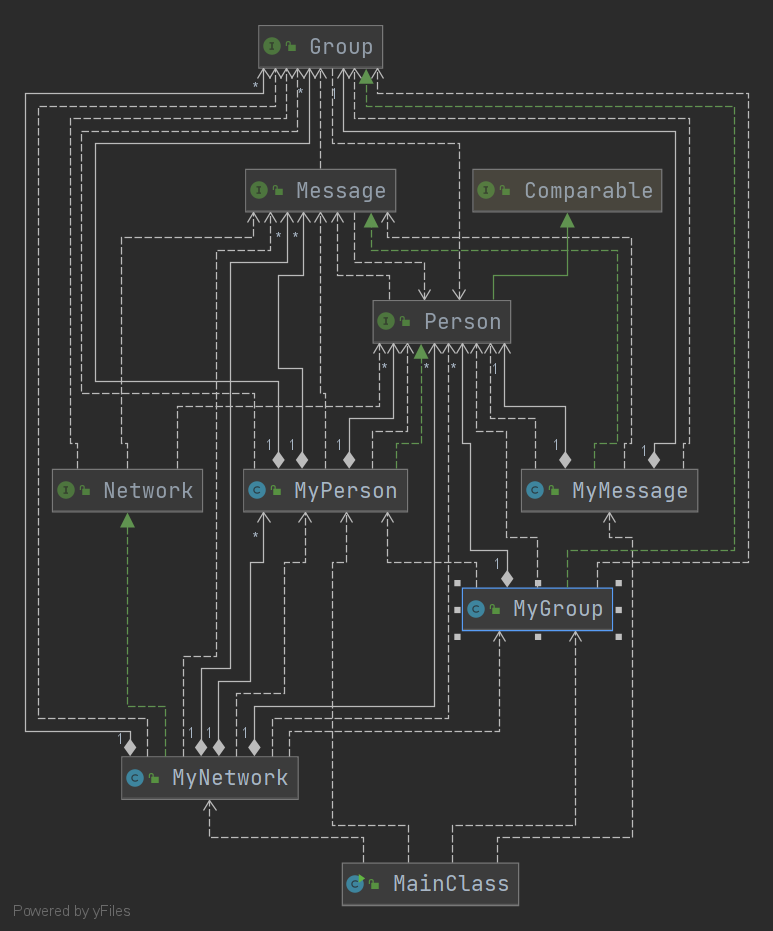
  • 第二次作业的架构仍然与JML规格提供结构保持一致。

第三次作业

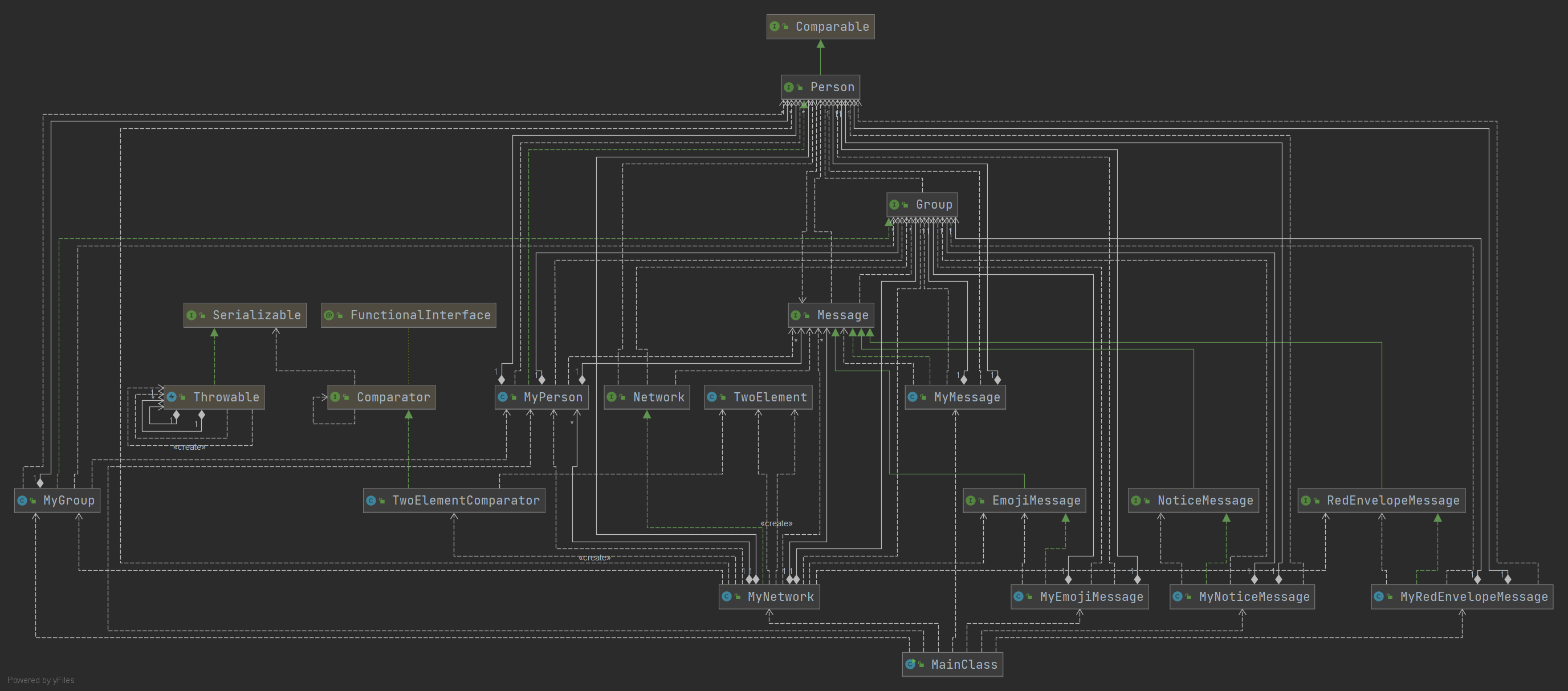
  • 如图所示，本次作业的结构与JML规格所提供的架构基本一致；有所变化的是，为了实现堆优化Dijkstra，新建了TwoElement类以及用于PriorityQueue比较的TwoElementComparator类。TwoElement类包含两个元素，如下：

    private int id;
private int value;

    而TwoElementComparator类通过比较value值的大小，来实现两个TwoElement对象的排序。

    两个类的新增，基本上不影响程序的架构清晰程度以及程序效率。

posted @ 2021-05-30 19:46  lazyc  阅读(126)  评论(0)    收藏  举报