旋转图像

初级算法 - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台

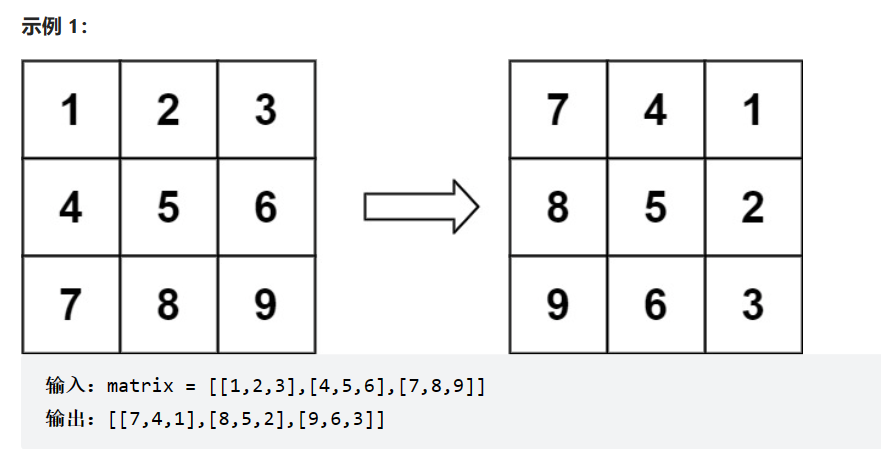
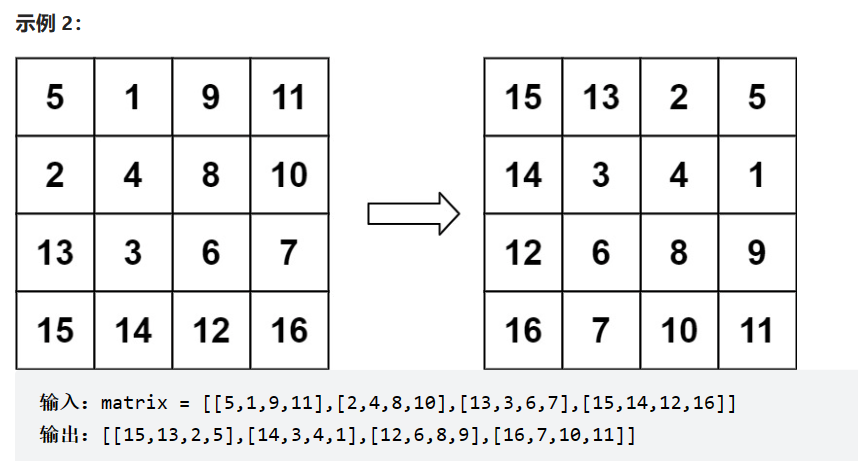
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

 

 

 方法一：使用辅助数组

算法思路，原数组的行旋转后成为该新数组的列，所以创建一个数组，将行数组添加进新数组列中

    
#实现方法一：
def rotate(self, matrix: List[List[int]]) -> None:
        new_list = []
        row = []
        for i in range(len(matrix)):
            for j in range(len(matrix)-1,-1,-1):
                row.append(matrix[j][i])
                if j-1 == -1:
                    new_list.append(row)
                    row = []
        matrix[:] = new_list[:]
实现方法二：

    def rotate(self, matrix: List[List[int]]) -> None:

        n = len(matrix)

        # Python 这里不能 matrix_new = matrix 或 matrix_new = matrix[:] 因为是引用拷贝

        matrix_new = [[0] * n for _ in range(n)]

        for i in range(n):

            for j in range(n):

                matrix_new[j][n - i - 1] = matrix[i][j]

        # 不能写成 matrix = matrix_new

        matrix[:] = matrix_new

时间复杂度：O(N^2)

空间复杂度：O(N^2)

 

方法二：原地旋转

def rotate(matrix):
    n = len(matrix)
    for i in range((n+1) // 2):
        for j in range((n) // 2):
            matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
            =   matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]


if __name__ == '__main__':
    matrix = [[5,1,9,11,61],[2,4,8,10,62],[13,3,6,7,63],[15,14,12,16,64],[65,66,67,68,69]]
    rotate(matrix)
    expect = [[65,15,13,2,5],[66,14,3,4,1],[67,12,6,8,9],[68,16,7,10,11],[69,64,63,62,61]]
    if matrix == expect:
        print("true")
    else:
        print("false")

时间复杂度：O(N^2)

空间复杂度：O(1)

注意：

1.

for i in range((n+1) // 2):

for j in range((n) // 2):
可以换成

for i in range(n // 2):

for j in range((n+1) // 2):

2.上述代码i、j的意义，可以认为是将矩阵分成四个小矩阵，ij分别代表小矩阵的行和列，遍历该小矩阵并且按照一定的规则替换其他小矩阵对应的值，当小矩阵遍历完后，大矩阵的值替换完成

，i+1或者是j+1是为了防止万一整体矩阵行列为奇数时，只用//2会漏掉一行一列

 

 

 

 

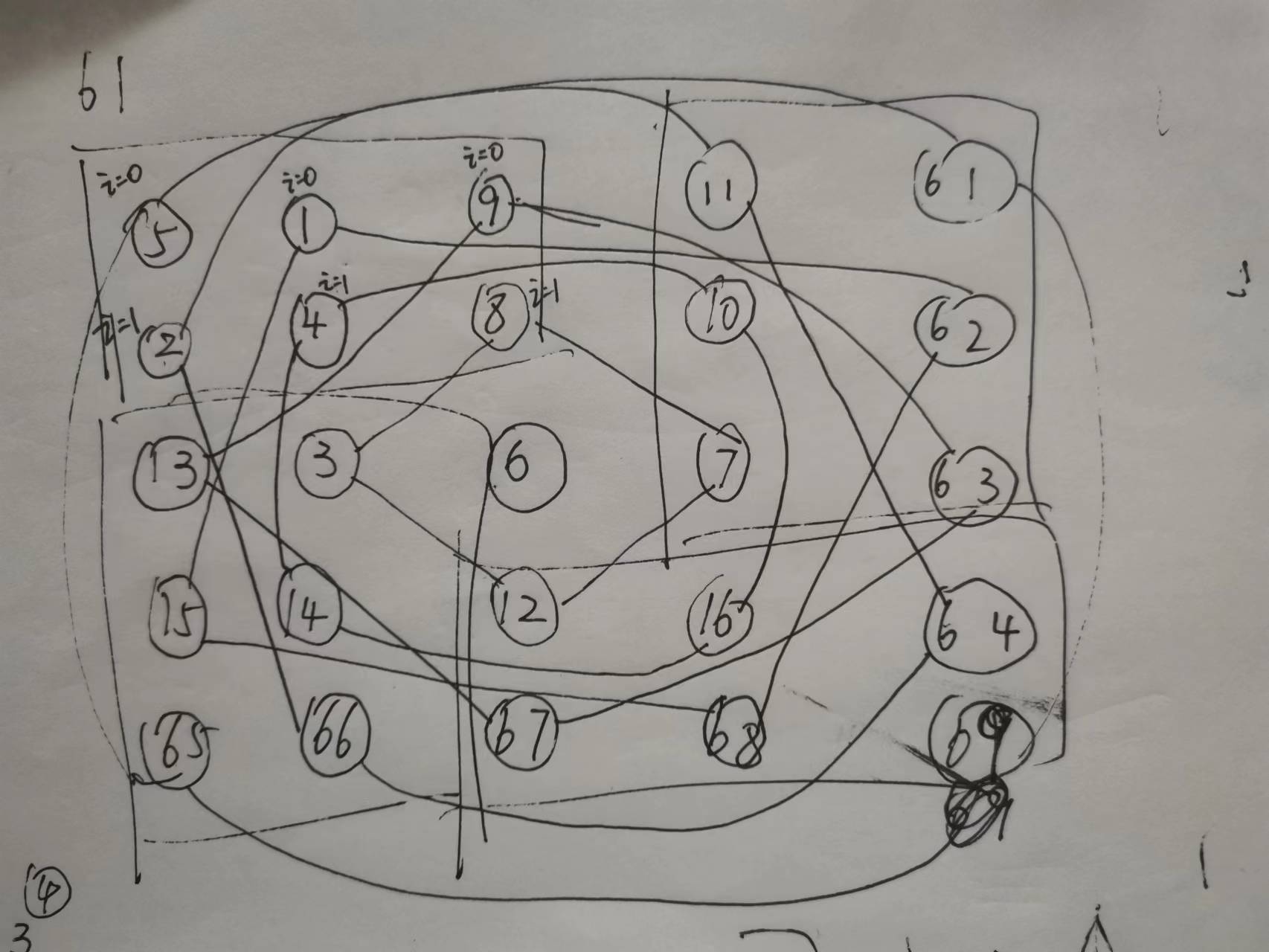
3.此处运用到元组的交换值，一定注意顺序逆时针，原来设计为顺时针导致翻转错误

            matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
            =   matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]

方法三：用翻转替代旋转

先水平反转，再主对角线反转

def rotate(matrix):
    l = len(matrix)
    for i in range(l // 2):
            matrix[i], matrix[l - i - 1] = matrix[l - i - 1], matrix[i]

    for i in range(l):
        for j in range(i):
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

时间复杂度：O(N^2)

空间复杂度：O(1)