1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。






2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
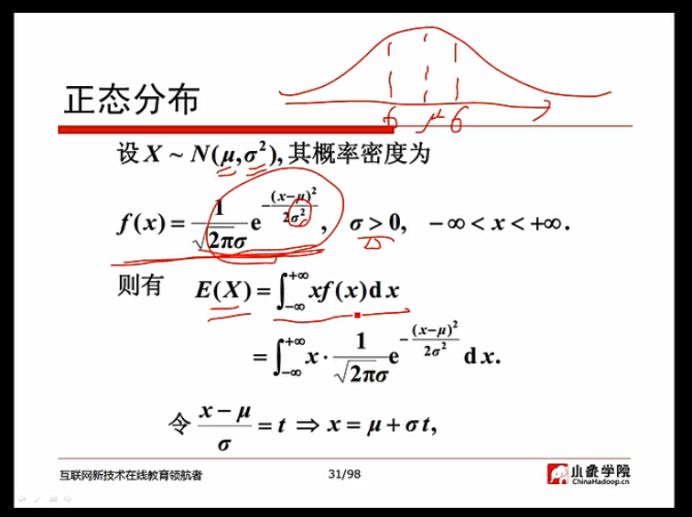
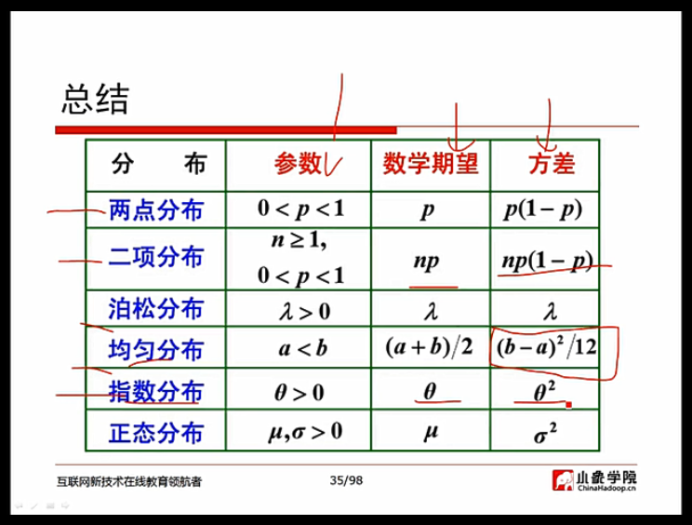
梯度:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。一般来说,梯度可以定义为一个函数的全部偏导数构成的向量(这一点与偏导数与方向导数不同,两者都为标量)。最主要的点为梯度向量的方向即为函数值增长最快的方向。
梯度下降:梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。简而言之就是得到函数的最优解,机器算法的说法是最小损失函数。
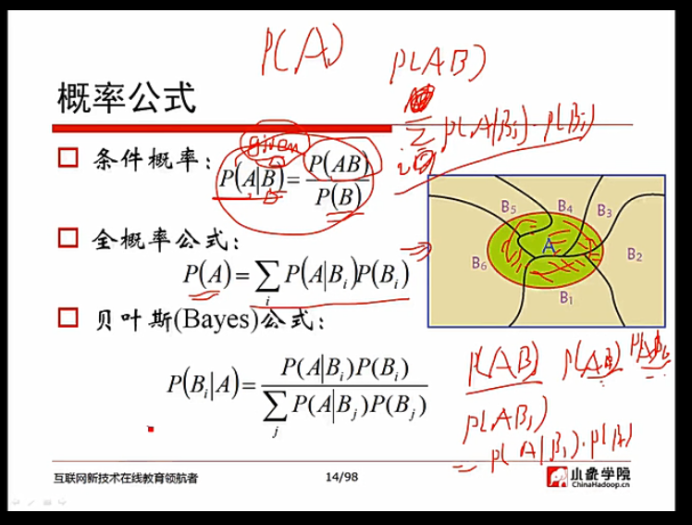
贝叶斯定理:贝叶斯定理也称贝叶斯推理,贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。简而言之就是用来描述两个条件概率之间的关系,结果与先验条件有很大关系,比如A事件下发生B事件的概率,与B事件下发生A事件的概率是不一样的。
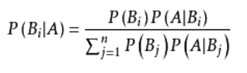


 浙公网安备 33010602011771号
浙公网安备 33010602011771号