P3740 [HAOI2014]贴海报

题目描述

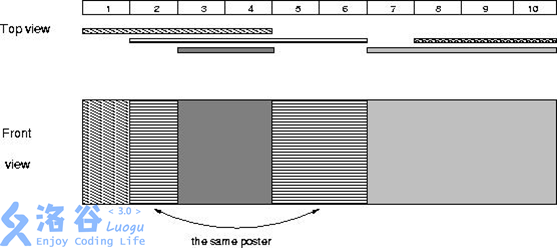
Bytetown城市要进行市长竞选，所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理，城市委员会为选民准备了一个张贴海报的electoral墙。

张贴规则如下：

1. electoral墙是一个长度为N个单位的长方形，每个单位记为一个格子；

2. 所有张贴的海报的高度必须与electoral墙的高度一致的；

3. 每张海报以“A B”表示，即从第A个格子到第B个格子张贴海报；

4. 后贴的海报可以覆盖前面已贴的海报或部分海报。

现在请你判断，张贴完所有海报后，在electoral墙上还可以看见多少张海报。

输入格式

第一行： N M 分别表示electoral墙的长度和海报个数

接下来M行: Ai Bi 表示每张海报张贴的位置

输出格式

输出贴完所有海报后，在electoral墙上还可以看见的海报数。

输入输出样例

输入 #1复制

100 5
1 4
2 6
8 10
3 4
7 10

输出 #1复制

4

说明/提示

【约束条件】

1 0<= N <= 10000000 1<=M<=1000 1<= Ai <= Bi <=10000000

所有的数据都是整数。数据之间有一个空格

---

 

法一：浮水法，数学思维（逆向思维）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
int flag=0,n,m,a[10000001][2];
int dfs(int x,int y,int now){
    if(flag==1) return 0;//这只是个优化！
    while(now<=m&&(y<a[now][0]||a[now][1]<x)) now++;
    if(now>m){
        flag=1;
        return 0;
    }
    if(a[now][0]<=y&&a[now][0]>x) dfs(x,a[now][0]-1,now+1);
    if(a[now][1]>=x&&a[now][1]<y) dfs(a[now][1]+1,y,now+1);
    return 0;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) scanf("%d%d",&a[i][0],&a[i][1]);
    int ans=1;
    for(int i=m-1;i>=1;i--){
        flag=0;
        dfs(a[i][0],a[i][1],i+1);
        if(flag==1) ans++;
    }
    printf("%d\n",ans);
}

 法二：离散化

这里要处理一个BUG

如果相邻+1，不相邻+2

防止出现↓

 

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
struct node{
    int val,num,type;
}dl[10000001];
int a[10000001][2];
int color[10000001],vis[10000001];
int cmp(node cmp_x,node cmp_y){
    return cmp_x.val<cmp_y.val;
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    int p=0;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&a[i][0],&a[i][1]);
        dl[++p].val=a[i][0];
        dl[p].num=i;
        dl[p].type=0;
        dl[++p].val=a[i][1];
        dl[p].num=i;
        dl[p].type=1;
    }
    sort(dl+1,dl+p+1,cmp);
    int P=0;
    for(int i=1;i<=p;i++){
        if(dl[i-1].val!=dl[i].val){
            if(dl[i-1].val+1!=dl[i].val) P+=2;
            else P++;
        }
        a[dl[i].num][dl[i].type]=P;
    }
    for(int i=1;i<=m;i++){
        for(int j=a[i][0];j<=a[i][1];j++) color[j]=i;
    }
    int l=0;
    for(int i=1;i<=1000000;i++){
        if(vis[color[i]]==0&&color[i]!=0){
            l++;
            vis[color[i]]=1;
        }
    }
    printf("%d",l);
}