【洛谷】P2421 [NOI2002]荒岛野人

传送门

 题目描述

克里特岛以野人群居而著称。岛上有排列成环行的 m 个山洞。这些山洞顺时针编号为 1,2,…,m 。岛上住着 n 个野人，一开始依次住在山洞 C_1,C_2​,…,Cn​中，以后每年，第 i 个野人会沿顺时针向前走 Pi个洞住下来。

每个野人 i 有一个寿命值 Li​，即生存的年数。

下面四幅图描述了一个有 6 个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为 1,2,3；每年要走过的洞穴数依次为 3,7,2；寿命值依次为 4,3,1。

 

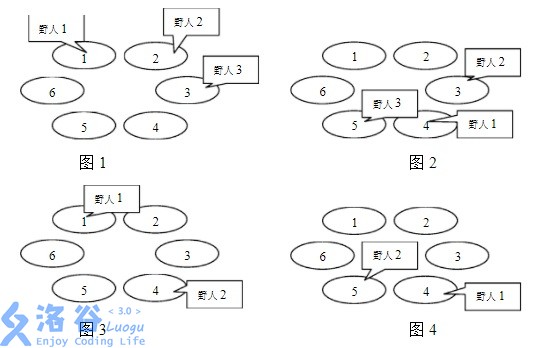
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入格式

第 1 行为一个整数 n(1≤n≤15)，即野人的数目。

第 2 行到第 N+1 每行为三个整数 Ci, Pi, Li (1≤ Ci,Pi ≤100, 0≤ Li ≤ 10^6 )，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式

仅包含一个数 M，即最少可能的山洞数。输入数据保证有解，且 M 不大于10^6。

输入输出样例

输入 #1
3
1 3 4
2 7 3
3 2 1
输出 #16

说明/提示

1≤N≤15，1≤Ci​,Pi​≤100，0≤Li​≤10^6

保证 M≤10^6

 

由题意得：如果两个野人（i,j）在x年处在同一个山洞 可列出此算式 C[i]+P[i]*x=C[j]+P[j]*x（mod M）=>C[i]+P[i]*x=C[j]+P[j]*x+y*M

化简可得：（P[i]-P[j]）*x-y*M=C[j]-C[i]   

所以可得   ax+by=c    a=P[i]-P[j]  b=M  c=C[j]-C[i]  然后求出最小的解(x*c%b+b)%b

如果在相遇之前，某个或全部野人寿命已尽，则成立（无解的话也成立）

 

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<sstream>
 5 #define Mod 19260817
 6 using namespace std;
 7 int X,Y;
 8 int Min(int XX,int YY){
 9     if(XX>YY) return YY;
10     return XX;
11 }
12 struct node{
13     int c,p,l;
14 }wild_man[10001];
15 int exgcd(int a,int b){
16     if(b==0){
17         X=1;
18         Y=0;
19         return a;
20     }
21     int gg=exgcd(b,a%b),t=X;
22     X=Y;
23     Y=t-(a/b)*Y;
24     return gg;
25 }
26 int check(int cave,node x,node y){
27     int A=y.p-x.p;
28     int B=cave;
29     int C=x.c-y.c;
30     int gcd=exgcd(A,B);
31     if(C%gcd!=0) return true;//无解
32     A/=gcd,B/=gcd,C/=gcd;
33     if(B<0) B=-B;
34     X=(X*C%B+B)%B;//最小值
35     if(X>Min(x.l,y.l)) return true;
36     return false;
37 }
38 int main(){
39     int n;
40     cin>>n;
41     int T=0;
42     for(int i=1;i<=n;i++){
43         cin>>wild_man[i].c>>wild_man[i].p>>wild_man[i].l;
44         if(T<wild_man[i].c) T=wild_man[i].c;
45     }
46     T--;
47     while(T<=1000000){//一遍遍枚举山洞数
48         T++;
49         int flag=0;
50         for(int i=1;i<=n;i++){
51             for(int j=1;j<i;j++){
52                 if(check(T,wild_man[i],wild_man[j])==false){
53                     flag=1;
54                     break;
55                 }
56             }
57             if(flag==1) break;
58         }
59         if(flag==1) continue;
60         cout<<T<<endl;
61         break;
62     }
63     
64 }

 

posted @ 2020-08-17 22:03  latent_Lin  阅读(144)  评论(0)    收藏  举报