几何

基本运算

内积

内积：\(a\cdot b=|a||b|\cos \theta\)。

定义 \(a=(a_x,a_y)\)，\(b=(b_x,b_y)\)。

那么 \(a\cdot b=|a||b|\cos \theta=(a_xi+a_yj)\cdot(b_xi+b_yj)=a_xb_x+a_yb_y\)。

叉积

叉积：\(a\times b=|a||b|\sin \theta\)。

那么 \(a\times b=|a||b|\sin \theta=(a_xi+a_yj)\times(b_xi+b_yj)=a_xb_y-a_yb_x\)。

求两线段交点

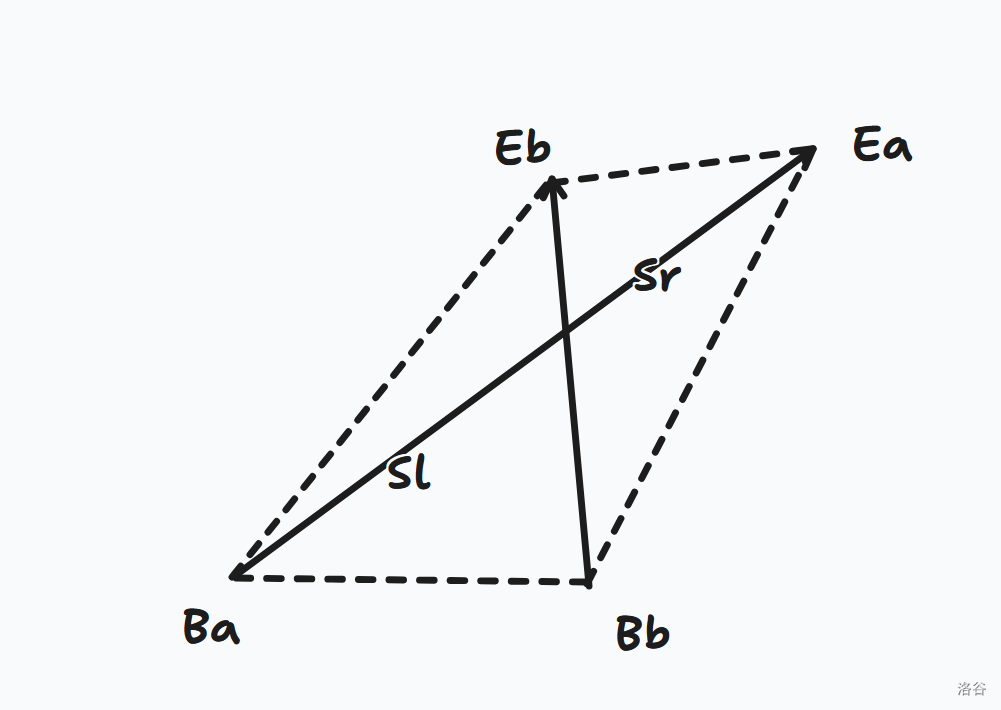
求出 \(\overrightarrow{B_aE_a}\) 和 \(\overrightarrow{B_bE_b}\) 的交点。

容易发现 \(B_aO:OE_a=S_{B_aE_bB_b}:S_{E_aE_bB_b}\)，那么用叉积求出两个三角性的面积即可。

极角

极角是向量与 \(x\) 轴的夹角弧长，范围 \([-\pi,\pi]\)。向量 \(a\) 的极角可以用 atan2(a_y,a_x) 求出。

平衡树线段比较

有时要用扫描线用平衡树维护当前的线段，保证所有线段只在端点处交。由于线段可能会在端点处交，那么不能只用一条线与其它线的交点的顺序比较，但可以用两条。但对于横向的线段要特判。

最近点对

最近点对可以用分治求出，先对点按照 \(x\) 坐标排序，二分处理 \([l,mid]\) 和 \([mid,r]\)，求出当前最近点对距离 \(A\)，然后处理 \([l,r]\)，首先只要考虑 \(|mid_x-p_x|\le A\) 的点 \(p\)，然后按照 \(y\) 坐标排序，发现只需要处理 \(y\) 轴距离小于 \(A\) 的点对，发现每个点要进行匹配的点为常数个，否则不满足已经求出来的 \(A\)。\(y\) 的排序可以使用归并排序，复杂度 \(O(n\log n)\)。

二维凸包

选出 \(y\) 坐标最小的点，将其设置成原点，然后将其它的点按极角排序。维护栈，当处理到点 \(a\)，如果 \(a,sta_{top},sta_{top-1}\) 形成的形状不符合（用叉积算出），那就弹出栈顶，一直进行到满足条件，最后将 \(a\) 加入到栈中。

当然再处理一些问题时要处理凸包上三点一线的情况，要把这种情况中的中间点去掉，不过也很好处理，直接选择挨个点，看它是否在上一个点和下一个点之间。

int tt = top;
top = 0;
for(int i = 0; i < tt; i++)
    if(get(sta[(i + tt - 1) % tt], sta[i], sta[(i + 1) % tt]) == 0 && ((p[sta[(i + tt - 1) % tt]].x <= p[sta[i]].x) == (p[sta[i]].x < p[sta[(i + 1) % tt]].x) || (p[sta[(i + tt - 1) % tt]].y <= p[sta[i]].y) == (p[sta[i]].y < p[sta[(i + 1) % tt]].y)))
    //先判断 i-1,i,i+1 是否在一条线上，再判断 i 是不是在 i-1 和 i+1 的中间，分别用坐标 x 和坐标 y 判断，就是为了特判这条线与 x 轴或 y 轴平行的情况。
        tag[i] = 1;
for(int i = 0; i < tt; i++)
    if(!tag[i])
        sta[top++] = sta[i];

旋转卡壳

经典问题就是求最远点对。

可以先求出凸包，然后枚举每条边 \((u,v)\)，找到与这条边重合的直线 \(p\)，往凸包的对面平移这条边直到触到边界，那么这个边界上的点中有是距离 \(u,v\) 最远的点，并且这个边界上的点最多有两个（一条边），可以根据叉积找到距离这条边最远的点就是边界上的点。

闵可夫斯基和

有两个点集合 \(A,B\)，求出 \(S=\{a+b|a\in A,b\in B\}\) 的凸包。发现是 \(A\) 的凸包的边和 \(B\) 的凸包的边按极角排序后的边集。

半平面交

将半平面按照极角排序，然后依次加入边，如果栈顶的边会被排除在外（根据交点判断）那么删除栈顶即可。

平面图找面

Problem：在平面上给一些点，将一些点进行连边，边只在端点处相交，这些边会将边划分成若干区域，求出每个区域。

容易发现区域的数量为 \(O(m)\)。将每个边分为两个方向，一个区域若干边的若干方向组成，这些边的方向是顺次连接的，两条相邻的边之间没有任何边，那么就容易处理了。

将每个点的边按极角排序，对于排完序后相邻的两条边将它们的不同方向连接起来。连完之后发现有若干个环，每个环就代表一个区域。

一般来说要去掉那个无限区域。如何找到无限区域？用叉积计算出面积为负数的区域就是无限区域。