LCT

LCT

LCT 用于解决动态树问题，可以理解为在正常的树剖能解决的问题的基础上增加了一项操作：断开并连接一些边，并强制在线。

我们来看 LCT 是怎么解决这类问题的。

实链剖分

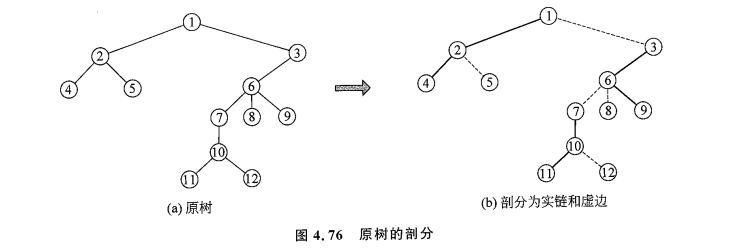
树剖中我们采用的是重链剖分，将树剖成一条条链，就可以把对树上路径的查询转化为不超过 \(\log n\) 条链的查询，从而提高了效率。那么 LCT 中我们依然考虑剖分，把树剖成一条条实链，实链和实链之间用虚边连接。

实链非常自由，不同于树剖中的重链，实链不一定要覆盖整棵原树，即使整棵树都是虚边也是合法的，只要虚边足够还原出树的路径形态即可。

辅助树

在 LCT 中，因为原树的形态是变化的，为了方便维护实链，我们把原树上的实链和虚边提取出来，建立一棵辅助树。辅助树和原树形态的差异不重要，但是辅助树可以还原出原树的路径特征，所以在代码中只需要存储和处理辅助树即可。

先来看实链的转换。实链在原树上是从上到下的一条路径，深度对应从小到大。以每个点的深度为其权值，可以把每一条实链转换为一棵 BST，这棵 BST 的中序遍历对应实链深度从小到大。至于剩下的虚边，只需连接在 BST 之间即可，具体连接到哪个节点不影响原树的路径形态。

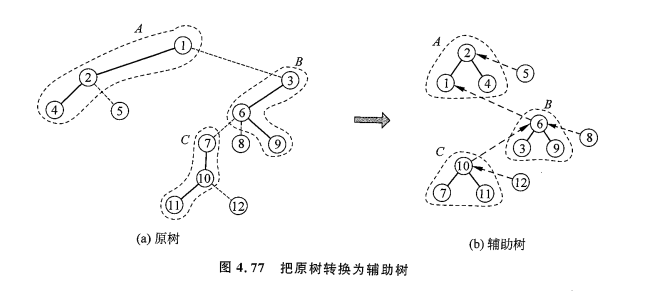
辅助树不唯一，但任意一种辅助树都可以还原出原树的路径特征，所以我们只需存储和处理辅助树。如果要查询两点间路径信息，可以在两点间建立实链，然后经过一番维护使辅助树仍然合法，最后这两个点在 BST 上的所有边合起来就是路径。

这里的 BST 一般采用 Splay 来维护，因为 Splay 的提根和旋转可以有效改善树的平衡性，并且实现很多关键操作。

LCT 的存储和操作

LCT 的存储是简单的：一个节点存储其父亲和两个儿子即可。

LCT 的操作有很多种，都作用在辅助树上，但目的是为了维护原树的形态。下面介绍一些常用操作：

• \(\text{splay}(x)\)：提根，在辅助树上把 \(x\) 旋转为它所在 Splay 树的根。

• \(\text{access}(x)\)：在原树上建立一条从根到 \(x\) 的实链。对应到辅助树上，就是重建一条从原树的根出发的 Splay 树。因为 \(x\) 是实链上最深的终点，所以执行完毕 \(\text{access}(x)\) 之后，\(x\) 位于 Splay 树的最右端。

  实现过程中，基本就是按照虚边从下往上走，建立新的实链，断开旧的实链。

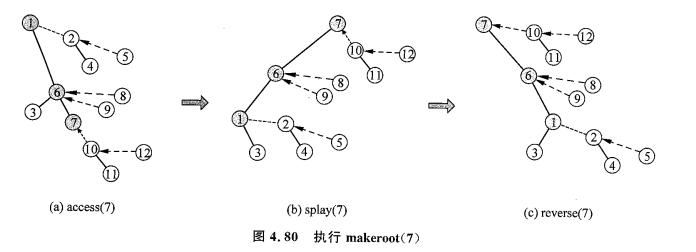
• \(\text{makeroot}(x)\)：把 \(x\) 在原树上旋转到根的位置。注意它的目的是为了改变原树的形态。执行完毕 \(\text{makeroot}(x)\) 之后，原树的形态发生改变。

  \(\text{makeroot}(x)\) 分为三步：\(\text{access}(x)\to\text{splay}(x)\to\text{reverse}(x)\)。简单说明：第一步，将 \(x\) 放到从根出发的实链上；第二步，把 \(x\) 旋转为根，但 \(x\) 此时仅仅在辅助树上变成了根，因为它还在 Splay 树的最右端，所以对应到原树上仍然是一个底层的点；第三步：以 \(x\) 为根翻转整棵辅助树，这样 \(x\) 就来到了 Splay 树的最左端，对应到原树上也就来到了根的位置。

• \(\text{findroot}(x)\)：查找 \(x\) 在原树上的根。这一函数用来判断两个节点是否连通。

  实现时，先调用 \(\text{access}(x)\) 使 \(x\) 和原树的根位于一条实链上，然后调用 \(\text{splay}(x)\) 使 \(x\) 翻转到 Splay 的根位置。由于原树的根此时深度最浅，肯定位于 Splay 的最左端，所以从 \(x\) 出发不断地跳左儿子即可。

• \(\text{split}(x,y)\)：建立一条从 \(x\) 到 \(y\) 的实链。用于统计 \(x\) 到 \(y\) 的信息。

  \(\text{split}(x,y)\) 分为三步：\(\text{makeroot}(x)\to\text{access}(y)\to\text{splay}(y)\)。第一步，使 \(x\) 成为原树的根；第二步，建立一条从根节点 \(x\) 到 \(y\) 的实链；第三步，把 \(y\) 旋转为 Splay 树的根。执行第三步的原因，一方面是为了方便进行 \(\text{cut}\) 操作，因为这样操作后的 \(y\) 只有左儿子，所以在 \(\text{cut}\) 时只需剪掉 \(y\) 的左儿子即可；另一方面是方便统计 \(x\) 到 \(y\) 的路径信息，这样操作之后路径信息就全在 \(y\) 上，查询 \(y\) 维护的信息即可。

• \(\text{link}(x,y)\)：在 \(x,y\) 之间建立一条边。

  先调用 \(\text{makeroot}(x)\) 使 \(x\) 成为原树的根，然后让 \(y\) 成为 \(x\) 的父亲即可。

• \(\text{cut}(x,y)\)：断开从 \(x\) 到 \(y\) 的边。

  在上文中已经提到，先执行 \(\text{split}(x,y)\)，然后剪掉 \(y\) 的左儿子即可。

• \(\text{isroot}(x)\)：判断 \(x\) 是否为它所在 Splay 树的根。

在进行上述操作的同时，如同树剖一样，可以顺便维护动态树上的信息。

复杂度

不难发现上述操作都基于 \(\text{access}(x)\)。而 \(\text{access}(x)\) 的复杂度和 Splay 树的深度有关，我们知道 Splay 树的深度是 \(\log n\) 的，所以 \(\text{access}(x)\) 的复杂度就是 \(O(\log n)\)，所以 LCT 单次操作的复杂度就是 \(O(\log n)\) 的。

P3690 【模板】动态树（LCT）

注意在单点修改时要先通过 \(\text{splay}(x)\) 将其转到根之后再修改，否则会影响 Splay 信息的正确性。

#include<bits/stdc++.h>
#define fw fwrite(obuf,p3-obuf,1,stdout)
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
#define putchar(x) (p3-obuf<1<<20?(*p3++=(x)):(fw,p3=obuf,*p3++=(x)))
using namespace std;

char buf[1<<20],obuf[1<<20],*p1=buf,*p2=buf,*p3=obuf,str[20<<2];
int read(){
	int x=0;
	char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x;
}
template<typename T>
void write(T x,char sf='\n'){
	if(x<0)putchar('-'),x=~x+1;
	int top=0;
	do str[top++]=x%10,x/=10;while(x);
	while(top)putchar(str[--top]+48);
	if(sf^'#')putchar(sf);
}
constexpr int MAXN=3e5+5;
struct{
	struct LCT{
		int fa,ch[2];
		int vl,sm,lz;
	}t[MAXN];
	#define ls(p) t[p].ch[0]
	#define rs(p) t[p].ch[1]
	#define fa(p) t[p].fa
	#define vl(p) t[p].vl
	#define sm(p) t[p].sm
	#define lz(p) t[p].lz
	bool isrt(int p){
		return ls(fa(p))!=p&&rs(fa(p))!=p;
	}
	void pushup(int p){
		sm(p)=vl(p)^sm(ls(p))^sm(rs(p));
	}
	void rev(int p){
		if(!p) return;
		swap(ls(p),rs(p));
		lz(p)^=1;
	}
	void pushdown(int p){
		if(!lz(p)) return;
		rev(ls(p)),rev(rs(p));
		lz(p)=0;
	}
	void update(int p){
		if(!isrt(p)) update(fa(p));
		pushdown(p);
	}
	int son(int p){
		return rs(fa(p))==p;
	}
	void rot(int p){
		int y=fa(p),z=fa(y);
		int k=rs(y)==p;
		if(!isrt(y)) t[z].ch[son(y)]=p;
		fa(p)=z;
		t[y].ch[k]=t[p].ch[k^1];
		if(t[p].ch[k^1]) fa(t[p].ch[k^1])=y;
		fa(y)=p;
		t[p].ch[k^1]=y;
		pushup(y);
	}
	void splay(int p){
		update(p);
		while(!isrt(p)){
			int f=fa(p);
			if(!isrt(f)) rot(son(f)==son(p)?f:p);
			rot(p);
		}
		pushup(p);
	}
	void access(int p){
		for(int x=0;p;x=p,p=fa(p)){
			splay(p);
			rs(p)=x;
			pushup(p);
		}
	}
	void mkrt(int p){
		access(p);
		splay(p);
		rev(p);
	}
	void split(int x,int y){
		mkrt(x);
		access(y);
		splay(y);
	}
	void link(int x,int y){
		mkrt(x);
		fa(x)=y;
	}
	void cut(int x,int y){
		split(x,y);
		if(ls(y)!=x||rs(x)) return;
		fa(x)=ls(y)=0;
		pushup(x);
	}
	int fndrt(int x){
		access(x);
		splay(x);
		while(ls(x)) pushdown(x),x=ls(x);
		return x;
	}
}T;

int main(){
	int n=read(),m=read();
	for(int i=1;i<=n;i++) T.t[i].vl=T.t[i].sm=read();
	while(m--){
		int op=read(),a=read(),b=read();
		switch(op){
			case 0:{
				T.split(a,b);
				write(T.t[b].sm);
				break;
			}case 1:{
				if(T.fndrt(a)!=T.fndrt(b)) T.link(a,b);
				break;
			}case 2:{
				T.cut(a,b);
				break;
			}default:{
				T.splay(a);
				T.t[a].vl=b;
				break;
			}
		}
	}
	return fw,0;
}