格拉姆-施密特正交化
在线性代数中,如果内积空间上的一组向量能够张成一个子空间,那么这一组向量就称为这个子空间的一个基。Gram-Schmidt正交化提供了一种方法,能够通过这一子空间上的一个基得出子空间的一个正交基,并可进一步求出对应的标准正交基。
这种正交化方法以Jørgen Pedersen Gram和Erhard Schmidt命名,然而比他们更早的拉普拉斯(Laplace)和柯西(Cauchy)已经发现了这一方法。在李群分解中,这种方法被推广为岩泽分解(Iwasawa decomposition)。
在数值计算中,Gram-Schmidt正交化是数值不稳定的,计算中累积的舍入误差会使最终结果的正交性变得很差。因此在实际应用中通常使用豪斯霍尔德变换或Givens旋转进行正交化。
记法
基本思想
Gram-Schmidt正交化的基本想法,是利用投影原理在已有正交基的基础上构造一个新的正交基。
设 。Vk是Vn上的k 维子空间,其标准正交基为
。Vk是Vn上的k 维子空间,其标准正交基为 ,且v不在Vk上。由投影原理知,v与其在Vk上的投影
,且v不在Vk上。由投影原理知,v与其在Vk上的投影 之差
之差
是正交于子空间Vk的,亦即β正交于Vk的正交基ηi。因此只要将β单位化,即
那么{η1,...,ηk+1}就是Vk在v上扩展的子空间span{v,η1,...,ηk}的标准正交基。
根据上述分析,对于向量组{v1,...,vm}张成的空间Vn,只要从其中一个向量(不妨设为v1)所张成的一维子空间span{v1}开始(注意到{v1}就是span{v1}的正交基),重复上述扩展构造正交基的过程,就能够得到Vn的一组正交基。这就是Gram-Schmidt正交化。
算法
首先需要确定扩展正交基的顺序,不妨设为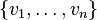 。Gram-Schmidt正交化的过程如下:
。Gram-Schmidt正交化的过程如下:
 |
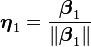 |
||
 |
 |
||
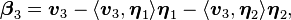 |
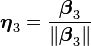 |
||
 |
 |
||
 |
 |
这样就得到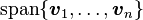 上的一组正交基
上的一组正交基 ,以及相应的标准正交基
,以及相应的标准正交基 。
。
- 例
考察如下欧几里得空间Rn中向量的集合,欧氏空间上内积的定义为<a, b> = bTa:
下面作Gram-Schmidt正交化,以得到一组正交向量:
下面验证向量β1与β2的正交性:
将这些向量单位化:
于是{η1,η2}就是span{v1, v2} 的一组标准正交基。
不同的形式
随着内积空间上内积的定义以及构成内积空间的元素的不同,Gram-Schmidt正交化也表现出不同的形式。
例如,在实向量空间上,内积定义为:
在复向量空间上,内积定义为:
函数之间的内积则定义为:
与之对应,相应的Gram-Schmidt正交化就具有不同的形式。
下载地址:http://www.mathworks.com/matlabcentral/fileexchange/12465-cgrscho
http://www.mathworks.com/matlabcentral/fileexchange/12495-mgrscho//修正版
原地址:http://blog.sina.com.cn/s/blog_495b66300100mrho.html



 :
: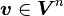 :
: :
: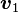 与
与 的
的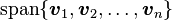 :
: 张成的
张成的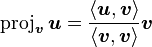 :
: 在
在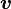 上的
上的


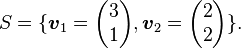


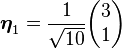
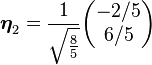


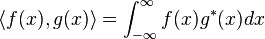

 浙公网安备 33010602011771号
浙公网安备 33010602011771号