python求矩阵的逆
文章目录
准备工作 Ready to work
环境 Environment
Anaconda 3 + Python 3.6.5 + Jupyter
模块导入 Module import
import numpy as np
import copy
from numpy.linalg import inv
代数余子式 Algebraic cofactor
定义 Definition
-
定义:在n阶行列式,把 ( i , j ) \;(i,j)\; (i,j)元 a i j \;a_{ij}\; aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做 ( i , j ) \;(i,j)\; (i,j)元 a i j \;a_{ij}\; aij的余子式,记作 M i j \;M_{ij}\; Mij 。
-
A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i+j}M_{ij} Aij=(−1)i+jMij 叫做 ( i , j ) (i,j) (i,j)元 a i j a_{ij} aij的代数余子式
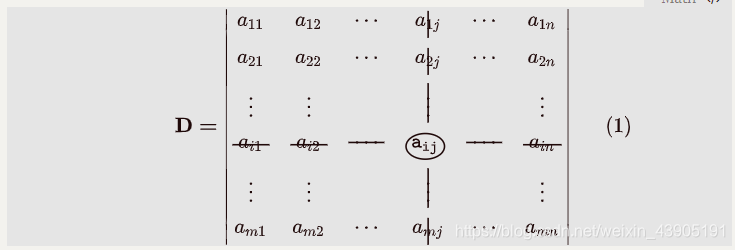
- D \bf D D中 ( i , j ) \;(i,j)\; (i,j)元 a i j \;\bf a_{ij}\; aij的余子式和代数余子式分别为:
M i j = ∣ a 11 a 12 ⋯ a 1 j − 1 a i j + 1 ⋯ a 1 n a 21 a 22 ⋯ a 2 j − 1 a 2 j + 1 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ ⋮ a i − 1 1 a i − 1 2 ⋯ a i − 1 j − 1 a i − 1 j + 1 ⋯ a i − 1 n a i + 1 1 a i + 1 2 ⋯ a i + 1 j − 1 a i + 1 j + 1 ⋯ a i + 1 n ⋮ ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m j − 1 a m j + 1 ⋯ a m n ∣ A i j = ( − 1 ) i + j M i j \bf M_{ij} = \begin{vmatrix} {a_{11}} & {a_{12}} & {\cdots} & {a_{1\;j-1}} & {a_{i\;j+1}} & {\cdots} & {a_{1n}}\\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2\;j-1}} & {a_{2\;j+1}} & {\cdots} & {a_{2n}}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ {a_{i-1\;1}} & {a_{i-1\;2}} & {\cdots} & {a_{i-1\;j-1}} & {a_{i-1\;j+1}} & {\cdots} & {a_{i-1n}}\\ {a_{i+1\;1}} & {a_{i+1\;2}} & {\cdots} & {a_{i+1\;j-1}} & {a_{i+1\;j+1}} & {\cdots} & {a_{i+1n}}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ {a_{m1}} & {a_{m2}} & {\cdots} & {a_{m\;j-1}} & {a_{m\;j+1}} & {\cdots} & {a_{mn}}\\ \end{vmatrix}\;\;\;\;A_{ij} = (-1)^{i+j}M_{ij} Mij=∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣a11a21⋮ai−11ai+11⋮am1a12a22⋮ai−12ai+12⋮am2⋯⋯⋯⋯⋯a1j−1a2j−1⋮ai−1j−1ai+1j−1⋮amj−1aij+1a2j+1⋮ai−1j+1ai+1j+1⋮amj+1⋯⋯⋯⋯⋯a1na2n⋮ai−1nai+1n⋮amn∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣Aij=(−1)i+jMij
代码实现 Code
余子式 Cofactor
| 先求出给定矩阵的余子式,即去除指定的行和列,然后根据公式求出代数余子式。
|
- 通过遍历实现,但不遍历整个矩阵。
变量说明:
- M:原始矩阵
- index:指定元素的索引,长度为2的向量
- temp:M中的每个行向量
- det():求行列式的函数
思路:
创建一个n-1阶的方阵(result)用于存放最后结果
通过遍历向result中按行赋值:
先判断是否为要消去的一行,如果是跳过本次循环
遍历原矩阵并取出其中的行向量
将行向量切片,以index[0]为界限且不包含index[0]
将两个一位矩阵片段拼接并对应放入result中
返回result行列式的值
def cof(M,index):
result = np.zeros((M.shape[0]-1,M.shape[1]-1))
for i in range(M.shape[0]):
temp = copy.deepcopy(M[i])
if i==index[0]-1:
continue
if i >= index[0]:
Ri = i-1
else:
Ri = i
result[Ri] = np.append(temp[:index[1]-1],temp[index[1]:])
return det(result)
- 通过numpy自带方法对矩阵进行重组
- 首先按照index的两个值作为x、y轴,对矩阵进行切片,将原始矩阵分为左上、右上、左下、右下四个矩阵
- 利用numpy.concatenate()函数对四个矩阵进行拼接:
- numpy.concatenate()有两个参数,第一个参数是矩阵列表,是要拼接的矩阵;第二个参数axis,axis=1表示对应行的数组进行拼接,axis=0表示对对应列进行拼接,默认为0
- 首先将左上、右上两个矩阵按行拼接组成结果矩阵的上半部分
- 同理求出结果矩阵的下半部分
- 最后将result的上下两部分按列拼接,返回result的行列式的值
def cof1(M,index):
zs = M[:index[0]-1,:index[1]-1]
ys = M[:index[0]-1,index[1]:]
zx = M[index[0]:,:index[1]-1]
yx = M[index[0]:,index[1]:]
s = np.concatenate((zs,ys),axis=1)
x = np.concatenate((zx,yx),axis=1)
return det(np.concatenate((s,x),axis=0))
代数余子式 Algebraic cofactor
- 参考公式
def alcof(M,index):
return pow(-1,index[0]+index[1])*cof(M,index)
伴随矩阵 Adjoint matrix
定义 Definition
- 定义:行列式 ∣ A ∣ \; \begin{vmatrix} A \end{vmatrix}\; ∣∣A∣∣的各个元素的代数余子式 A i j \;A_{ij}\; Aij构成的矩阵。
a d j ( C ) = [ A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋮ A 1 n A 2 n ⋯ A n n ] A i j 是 C i j 的 代 数 余 子 式 adj(\bf C) = \begin{bmatrix} A_{11} & A_{21} & \cdots & A_{n1}\\ A_{12} & A_{22} & \cdots & A_{n2}\\ \vdots & \vdots && \vdots\\ A_{1n} & A_{2n} & \cdots & A_{nn}\\ \end{bmatrix} \;\;\;\;\;\;\;\;\;\;\;A_{ij}是C_{ij}的代数余子式 adj(C)=⎣⎢⎢⎢⎡A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1An2⋮Ann⎦⎥⎥⎥⎤Aij是Cij的代数余子式
称为C的伴随矩阵,简称伴随阵,记作 C ∗ 。 C^*。 C∗。
伴随矩阵满足:
- A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = \begin{vmatrix}A \end{vmatrix}E AA∗=A∗A=∣∣A∣∣E
代码实现 Code
- 分析公式可以看出伴随矩阵的形状与原始矩阵相同,伴随矩阵(i,j)位置上的元是原始矩阵(j,i)位置上元的代数余子式
思路:
- 创建一个与原始矩阵形状相同的矩阵result
- 通过向result中填充数据
- 注:矩阵下标从1开始,而在代码中索引均从0开始
def adj(M):
result = np.zeros((M.shape[0],M.shape[1]))
for i in range(1,M.shape[0]+1):
for j in range(1,M.shape[1]+1):
result[j-1][i-1] = alcof(copy.deepcopy(M),[i,j])
return result
矩阵的逆 Inverse of matrix
定义 Definition
- 定义:对于n阶矩阵A,如果有一个n阶矩阵B使其满足以下条件,则说矩阵A是可逆的,B是A的逆矩阵,简称逆阵。
A B = B A = E \bf AB=BA=E AB=BA=E
-
A的逆记作 A − 1 \bf A^{-1} A−1
-
定理1:若矩阵A可逆,则 ∣ A ∣ ≠ 0 \bf \begin{vmatrix} A\end{vmatrix} \neq 0 ∣∣A∣∣=0
-
定理2:若 ∣ A ∣ ≠ 0 \bf \begin{vmatrix} A\end{vmatrix} \neq 0 ∣∣A∣∣=0,则A可逆,且:
A − 1 = 1 ∣ A ∣ A ∗ \bf A^{-1} = \frac{1}{\begin{vmatrix} A \end{vmatrix}}A^* A−1=∣∣A∣∣1A∗
- 推论:若 A B = E ( \bf AB=E( AB=E(或 B A = E ) \bf BA=E) BA=E),则 B = A ∗ \bf B=A^* B=A∗
代码实现 Code
- 根据公式原始矩阵对应行列式的值的倒数乘该矩阵的伴随矩阵
def invmat(M):
if det(M)!=0:
return 1/det(M)*adj(M)
else:
print(原始矩阵不能为0)
测试 程序 Test program
- 可以调用numpy.linalg.inv()函数来求得原始矩阵的逆,然后调用自己的函数,看两个输出结果是否相同
from numpy.linalg import inv
M = np.array([[1,2,-1],[2,3,4],[3,1,2]])
print(inv(M))
print(invmat(M))



 浙公网安备 33010602011771号
浙公网安备 33010602011771号