第三节

DP(Dynamic Programming)动态规划

1. 01背包问题：

#include<iostream>
using namespace std;
int n, W;
const int MAX = 105;
int w[MAX], v[MAX];



//1.递归  O(2的n次幂)
//正在选第i个物品   j 为总重量W-已经做出选择的i-1个物品的重量
int dfs(int i, int j)
{
    //返回最大价值和
    int res = 0;

    //如果选完了n-1个  那么无论再怎么选价值都必定为0
    if (i == n)
    {
        res = 0;
    }
    //如果该物品超重
    else if (j < w[i])
    {
        res = dfs(i + 1, j);
    }//如果不超重
    else 
    {
        res = max(dfs(i + 1, j), dfs(i + 1, j - w[i]) + v[i]);
    }

    return res;
}

//2.记忆化搜索  常规dfs 有太多重复递归调用
//不妨考虑用一个数组来存放   使重复值只计算一次
const int W_MAX = 1000;
int dp[MAX + 1][W_MAX + 1];
int dfs1(int i, int j)
{
    //如果计算过 直接用结果
    if (dp[i][j] >= 0)
    {
        return dp[i][j];
    }
    //否则再计算
    int res;
    if (i == n)
    {
        res = 0;
    }
    else if (j < w[i])
    {
        res = dfs1(i + 1, j);
    }
    else
    {
        res = max(dfs1(i + 1, j), dfs1(i + 1, j - w[i]) + v[i]);
    }

    //将结果记录在dp数组中
    dp[i][j] = res;
    return res;
}

//3 动态规划
//利用循环  而不是递归  来给dp数组赋值
void solve()
{
    ////首先 dp[n][j]=0
    //for (int j = 0; j < n; j++)
    //    dp[n][j] = 0;
    // 
    memset(dp, 0, sizeof(dp));
    //利用循环赋值
    for (int i = n - 1; i >= 0; i--)
    {
        for (int j = 0; j <= W; j++)
        {
            if (j >= w[i])
            {
                dp[i][j] = max(dp[i + 1][ j], dp[i + 1][j - w[i]] + v[i]);
            }
            else
            {
                dp[i][j] = dp[i + 1][j];
            }
        }
    }
}

//4.正向递推
void solve1()
{
    //dp[i][j]  代表已经选择i-1个物品  总重不能超过j
    //dp[i][j]的值为 已选i-1，总重不能超过j 的最大价值
    memset(dp, 0, sizeof(dp));
    //所以dp[0][]=0

    //不能选 dp[i+1][j]=dp[i][j]
    //能选   dp[i+1][j]=max(dp[i][j],dp[i][j+w[i]]+v[i])
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= W; j++)
        {
            if (j < w[i])
            {
                dp[i + 1] [j] = dp[i][j];
            }
            else
            {
                dp[i + 1][j] = max(dp[i][j], dp[i][j -w[i]] + v[i]);
            }
        }
    }

    
}

int main()
{
    cin >> n >> W;
    for (int i = 0; i < n; i++)cin >> w[i] >> v[i];

    //cout << dfs(0, W);

    memset(dp, -1, sizeof(dp));//逐个字节赋值-1的二进制  使得都为-1
    /*cout << dfs1(0, W);*/
    //solve();
    //cout << dp[0][W];

    solve1();
    cout << dp[n][W];
    return 0;
}

2. 最长公共子序列

#include<iostream>
#include<string.h>
using namespace std;
int m,n;
const int MAX=1e3+5;
char s[MAX],t[MAX];
int dp[MAX+1][MAX+1];
//dp[i][j] i:s串序列尾(s1,s2,s3...si) j:t串序列尾(t1,t2,t3...tj) 代表s和t在这种长度下公共子序列最大长度
//dp[0][] =0  dp[][0] =0
void solve()
{
    //不妨全设置为0算了
    memset(dp,0,sizeof(dp));
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<n;j++)
        {
            //如果两串末尾序列 si=tj  显然dp[i+1][j+1]=dp[i][j]+1;
            //否则 dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1]);
            if(s[i]==t[j])
            {
                dp[i+1][j+1]=dp[i][j]+1;
            }
            else
            {
                dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1]);
            }
        }
    }
}
int main()
{
    cin>>m>>n;
    for(int i=0;i<m;i++)cin>>s[i];
    for(int i=0;i<n;i++)cin>>t[i];

    solve();
    cout<<dp[m][n];
    return 0;
}

3.完全背包

#include<iostream>
#include<string.h>
using namespace std;
int n,W;
const int N_MAX=105,W_MAX=1e4+5;
int w[N_MAX],v[N_MAX],dp[N_MAX][W_MAX];

//dp[i][j]  代表正在选第i个物品 选择完前i-1个物品 总重不能超过j时  的最大价值
//那么  dp[0][]=0   
//当j>w[i]  可以选择   ge=j/w[i]  dp[i+1][j]=max(dp[i][j],dp[i][j+w[i]*k]+v[i]*k)  0<=k<=ge
//j<w[i]   不可         dp[i+1][j]=dp[i][j]
void solve()
{
    //不妨均给予初值0
    memset(dp,0,sizeof(dp));
    //给dp数组填值
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=W;j++)
        {
           
            if(j<w[i])
            {
                dp[i+1][j]=dp[i][j];
            } 
            else 
            {
                int ge=j/w[i];
                for(int k=0;k<=ge;k++)
                {
                    //有关减号的理解  选前i个物品总重不超过j 的最大价值
                    //              应该等于 从前i-1个物品选总重不超过 j-w[i]*k 的最大价值再加上这k个物品的价值
                    dp[i+1][j]=max(dp[i+1][j],dp[i][j-k*w[i]]+v[i]*k);
                }
            }
        }
    }
}

void solve1()
{
    //针对于dp[i+1][j]选k   和dp[i+1][j-w[i]]选k-1   结果一样
    //所以 有很多的数组被重复的填值  并且  无论k循环多少次  总有一个dp[i+1][j]与之对应  所以不循环也行

    memset(dp,0,sizeof(dp));
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=W;j++)
        {
            if(j<w[i])
            {
                dp[i+1][j]=dp[i][j];
            }else 
            {
                ////// 此处注解见下面
                dp[i+1][j]=max(dp[i][j],dp[i+1][j-w[i]]+v[i]);
            }
        }
    } 
}

int main()
{
    cin>>n>>W;
    for(int i=0;i<n;i++)cin>>w[i]>>v[i];


    solve1();
    cout<<dp[n][W];
    return 0;
}

注意：

max{ dp[i][j], max{ dp[i][ ( j - w[i] ) - k * w[i] + k * v[i] | 0 <= k } + v[i] }在k * w[i]后面少了个"]"，

改为max{ dp[i][j], max{ dp[i][ ( j - w[i] ) - k * w[i] ] + k * v[i] | 0 <= k } + v[i] }

也因此：我们自然而然得到第一个等式：不选与至少选1个比较最大

　　　　第二个：由于 dp[i][j]选k个与dp[i] [j-w[i]] 选k-1 个一样，我们尽量往dp[i][ j-w[i]]让靠拢

　　　　　　　　dp[i][j] 至少选1个转化为 dp[i] [j-w[i]] 选或不选 +v[i]

　　　　第三个：　而显然 dp[i] [j-w[i]] 选或不选的最大值即为 dp[i+1][j-w[i]]

　　也因此得到 dp[i+1][j] =max( dp[i][j] , dp[i +1][j-w[i]]+v[i] )

4. 01背包之2

此处我们应当注意，wi 值远大于 vi ，所以我们dp[i][j] j代表重量不若 j代表价值

#include<iostream>
#include<cstring>
using namespace std;
int n,W;
const int N_MAX=105,V_MAX=100,Value_SUM_MAX=N_MAX*V_MAX;
int w[N_MAX],v[N_MAX],dp[N_MAX][Value_SUM_MAX+1];
//！！！！！！！！！！！！
//加一的必要性  j要从0开始的到MAX啊  此处是长度


//dp[i][j]代表  前i-1 个物品的价值为j时重量的最小值
// dp[0][0]=0         其他    dp[0][]=INF（不存在）  而dp[n][>V_SUM]=INF
// if(j<v[i]) dp[i+1][j]=dp[i][j]
//  否则  dp[i+1][j]=min(dp[i][j],dp[i][j-v[i]]+w[i])
//最终输出 dp[n][v的和]


void solve()
{
    memset(dp,0x3f,sizeof(dp));
    // cout<<dp[0][0];  1061109567   >  W
    dp[0][0]=0;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=Value_SUM_MAX;j++)
        {
            if(j<v[i])
            {
                dp[i+1][j]=dp[i][j];
            }else
            {
                dp[i+1][j]=min(dp[i][j],dp[i][j-v[i]]+w[i]);
            }

        }
    }


    int res=0;
    //遍历数组 找到最大的价值

    for(int i=0;i<=Value_SUM_MAX;i++)
    {
        if(dp[n][i]<=W)
        {
            //随着价值增大 重量必定增大 当重量大于W便停止更新
            res=i;
        }
    }
    printf("%d",res);
}

int main()
{
    cin>>n>>W;
    for(int i=0;i<n;i++)
    {
        cin>>w[i]>>v[i];
    }
    solve();
    
    return 0;
}

5.多重部分和问题

#include<iostream>
using namespace std;
#include<cstring>
int n,K;
const int N_MAX=105,K_MAX=1e5,INF=0x3f;
int a[N_MAX],m[N_MAX],dp[N_MAX][K_MAX+1];

//dp[i][j]  表示 前i-1个数和为j  的可行性   
// 0假 1真 
// dp[i][j]=    dp[i-1][j-ge*a[i]]
void solve1()           
{
    //O ( n*K*sum_m ) 
    memset(dp,0,sizeof(dp));
    dp[0][0]=1;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=K_MAX;j++)
        {
            for(int x=min(j/a[i],m[i]);x>=0;x--)
            {
                dp[i+1][j]=max(dp[i][j-x*a[i]],dp[i+1][j]);   //超时了  
            }
            
            //dp[i][j-x*a[i]]  x>=1 
            //== dp[i][j-a[i]-x*a[i]]  x>=0   ==dp[i+1][j-a[i]]
        
            // if(j<a[i])
            // {
            //     dp[i+1][j]=dp[i][j];
            // }else if(j>=a[i]&&j/a[i]<=m[i])
            // {
            //     dp[i+1][j]=max(dp[i][j],dp[i+1][j-a[i]]); 
            // }  错了
            
            
        }
    }
    if(dp[n][K]==1)cout<<"Yes";
    else cout<<"No";
}

//dp[i+1][j] 表示用 前i个数凑成和j  后剩余第i个数最多有几个 （无法凑成  设置值为-1
//那么 
//    考虑不选  1. 当dp[i][j]>=0  dp[i+1][j]=m[i]
//               2.当j<a[i] 或者说dp[i+1][j-a[i]]<=0  dp[i+1][j]=-1
//              考虑 当dp[i][j]>=0时  假若j<a[i] dp[i+1][j]还是要为m[i]呀  所以优先级
//    在考虑选  dp[i+1][j]=dp[i+1][j-a[i]]-1
// memset -1   dp[][0]=0

int dp2[K_MAX+1];

void solve2()
{
    memset(dp2,-1,sizeof(dp2));
    dp2[0]=0;

    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=K_MAX;j++)
        {
            // if(j<a[i]||dp2[j-a[i]]<=0)
            // {
            //     dp2[j]=-1;
            // }else if(dp2[j]>=0)
            // {
            //     dp2[j]=m[i];
            // }else
            // {
            //     dp2[j]=dp2[j-a[i]]-1;
            // }
            
             if(dp2[j]>=0)
            {
                dp2[j]=m[i];
            }else if(j<a[i]||dp2[j-a[i]]<=0)
            {
                dp2[j]=-1;
            }
            else
            {
                dp2[j]=dp2[j-a[i]]-1;
            }
        }
    }
    if(dp2[K]>=0)
    {
        cout<<"Yes";
    }else
    {
        cout<<"No";
    }
}

int main()
{
    cin>>n>>K;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<n;i++)cin>>m[i];

    solve2();

    return 0;
}

6.最长上升子序列问题

介绍：lower_bound 和 upper_bound

#include<iostream>
using namespace std;
#include<cstring>
const int MAX=1e3+5;
int n,a[MAX];
int dp[MAX+1];
//dp[j]代表以a[j]结尾的 子序列的最大长度
//dp[j]包括 a[j]本身  ||1||  和 ||dp[i]+1|i<j&&a[i]<a[j]||  如果a[j]前面 存在更小的a[i] dp[j]=dp[i]+1
// dp[j]=max{1,dp[i]+1|i<j&&a[i]<a[j]}
 void solve()
{
    for(int i=0;i<n;i++)
    { 
        dp[i]=1;    
        for(int j=0;j<i;j++)
        {
           if(a[j]<a[i])
           {
               dp[i]=max(dp[i],dp[j]+1);
           }
        }
    }
    int res=0;
    for(int i=0;i<n;i++)
    {
        res=max(res,dp[i]);
    }
    cout<<res;
}

// //我们考虑 dp[i] 代表长度为i+1的最长上升子序列的最小的末尾值
// //显然不存在 则为INF   当i=0||dp[i-1]<a[j]时  dp[i]=min(dp[i],a[j]);
// void solve2()
// {
//     const int INF=0x3f3f3f3f;
//     fill(dp,dp+n,INF);

//     for(int i=1;i<n;i++)
//     dp[0]=min(dp[0],a[i]);

//     for(int i=1;i<n;i++)
//     {
//         for(int j=i+1;j<n;j++)
//         {
//             if(dp[i-1]<a[j])
//             {
//                 dp[i]=min(dp[i],a[j]);
//             }
//         }
//     }
//     int res=0;
//     for(int i=0;i<n;i++)
//     {
//         if(dp[i]<INF)
//         {
//             res=i+1;
//         }
//     }
//     cout<<res;
// }   有问题！！！！！

void solve3()
{
    memset(dp,0x3f,sizeof(dp));
    for(int i=0;i<n;i++)
    {
        *lower_bound(dp,dp+n,a[i])=a[i];
    }
    printf("%d\n",lower_bound(dp,dp+n,0x3f3f3f3f)-dp);
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    solve3();
    return 0;
}

7.划分数

dp不仅对于求解最优问题有效，对于各种排列组合的个数概率期望之类的计算也很有用

#include<iostream>
using namespace std;

int n,m,M;
//我们假设 n =6  m=4 
// 0 0 0 6
// 0 0 1 5   0 0 2 4  0 0 3 3
// 0 1 1 4   0 1 2 3  0 2 2 2 
// 1 1 1 3   1 1 2 2  
// 定义 dp[i][j] 为 i的j划分的方法数%M   
// 将问题等价为 划分成m组（可填0）
//那么 dp[i][j] 也就 等于 
// 有0  006 015 024 033 114 123 222  恰好为dp[i][j-1]
//无0  1113 1122  这里采用一种巧妙地方法 0002  0011  转化为了dp[i-j][j]

//所求为 dp[n][m]%M     dp[0][0]=1
const int MAX=1e3+5;
int dp[MAX][MAX];
void solve()
{
    //  0 0 4
    //  0 1 3   0 2 2
    //  1 1 2   
    // memset(dp,0,sizeof(dp));
    dp[0][0]=1;

    for(int i=0;i<=n;i++)//注意dp[0][]=1
    {
        for(int j=1;j<=m;j++)
        {
            if(i-j>=0)
            {
                 dp[i][j]=(dp[i-j][j]+dp[i][j-1])%M;//此处取模 避免溢出？
            }else{
                dp[i][j]=dp[i][j-1];
            }
           
        }
    }
    cout<<dp[n][m];
}

int main()
{
    cin>>n>>m>>M;
    solve();
    return 0;
}

8.多重集组合数

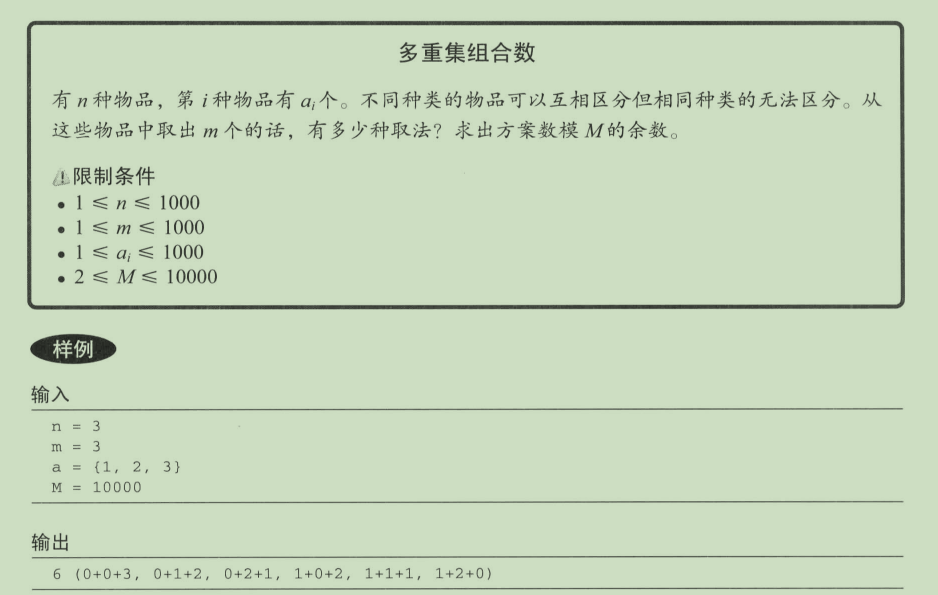
#include<iostream>
using namespace std;
#include<cstring>
int n,m,M;
const int MAX=1e3+5;
int a[MAX];
//dp[i+1][j] 从前i种物品取j个的取法组合总数
// 3 3
// 1 2 3
// 122  123 223 233 333 133
// dp[i+1][j]=取k个i  + dp[i][j-k]    k<=a[i]&&k<=j
// 即dp[i+1][j]=sum(dp[i][j-k]  k<=a[i]&&k<=j)
// 这样 O(nm*m)
// 而sum(dp[i][j-k]  k>=0 k<=a[i]&&k<=j)= dp[i][j] + sum(dp[i][j-k] k>=1&&...)
// 要知道 sum(dp[i][j-1-k] k>=0&&k<=j-1&&k<=a[i]) -dp[i][j-1-a[i]] == dp[i+1][j-1]-dp[i][j-1-a[i]]
// == sum(dp[i][j-k] k>=1&&k<=a[i]&&k<=j)

//综上  dp[i+1][j]=dp[i][j]+dp[i+1][j-1]-dp[i][j-1-a[i]]
// dp[n][m] 
int dp[MAX][MAX];
void solve()
{
    // memset(dp,0,sizeof(dp));
    //并且一个都不取得方法数为0
    for(int i=0;i<=n;i++) dp[i][0]=1;

    for(int i=0;i<n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(j-1-a[i]>=0)
            {
                dp[i+1][j]=(dp[i][j]+dp[i+1][j-1]-dp[i][j-1-a[i]]+M)%M;//直接取模避免溢出
                //因为减号  所以还要加M 避免出现负数
            }else
            {
                dp[i+1][j]=(dp[i][j]+dp[i+1][j-1])%M;
            }
        }
    }
    cout<<dp[n][m];
}

int main()
{
    cin>>n>>m>>M;
    for(int i=0;i<n;i++)cin>>a[i];

    solve();
    return 0;
}

存在许多问题，之后二刷再改正。。。

posted @ 2022-07-23 19:28 蓝色的a猫阅读(79) 评论(0) 收藏举报

刷新页面返回顶部

lansedemao

第三节