2.2

2.2 贪心法

2.2.1 硬币问题

 

 很容易想出：从最大的硬币开始选，每次都选出尽可能多的硬币，然后再选更小的

#include<iostream>
using namespace std;
int arr[6];
int a;
int t;
const int c[6]={1,5,10,50,100,500};
void solve()
{
    int res=0;
    for(int i=5;i>=0;i--)
    {
        //个数为所拥有的和  所能有的的最小值
        int ge=min(arr[i],a/c[i]);
        res+=ge;
        a-=ge*c[i];
    } 
    cout<<res<<endl;
}

int main()
{
    cin>>t;
    while(t--)
    {
        for(int i=0;i<6;i++)cin>>arr[i];

        cin>>a;

        solve();
    }

    return 0;
}

 

2.2.2 区间问题

 

 

 

 

 

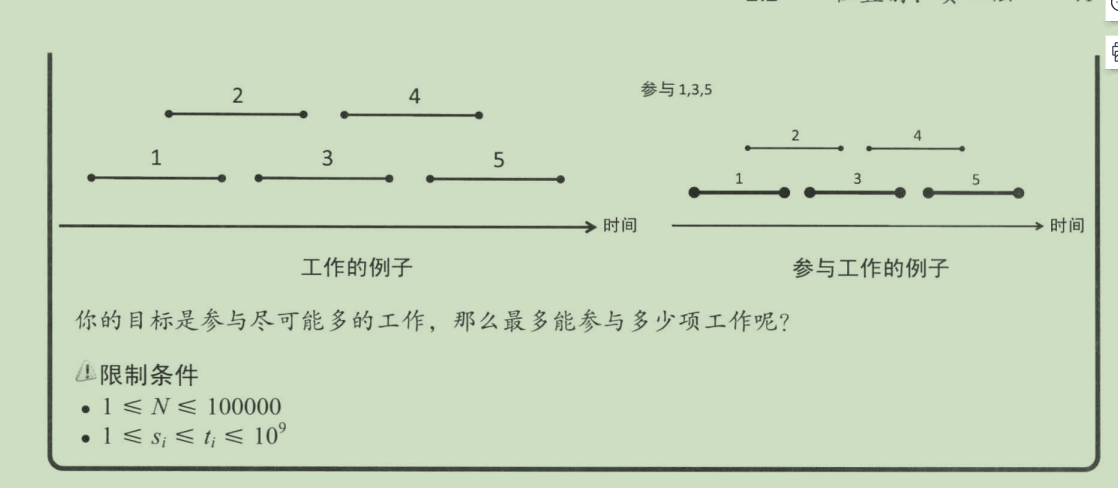
(1)、每次选取开始时间最早的；                      ------------------------

　　　　　　　　　　　　　　　　　　　　　　----     -----

(2)、每次选取结束时间最早的；

 

(3)、每次选取用时最短的；                          ---------  ------  --------

　　　　　　　　　　　　　　　　　　　　----           ----

对于上面的算法，只有算法(2)是正确的，其它的两种都可以找到相应的反例。

#include<iostream>
#include<algorithm>
using namespace std;
int n;
const int MAX=1e5;
int start[MAX] , myend[MAX];
pair<int ,int> p[MAX];
//选择结束时间最早的
void solve()
{
    //按结束时间先后排序
    for(int i=0;i<n;i++)
    {
        p[i].first=myend[i];
        p[i].second=start[i];
    }
    sort(p,p+n);
   
    int res=0,t=0;//t是当前时间
    for(int i=0;i<n;i++)
    {
        //优先排好序后 按照顺序结束时间早的排在前面
        //所有只要能选   就直接选
        if(t<p[i].second)
        {
            res++;
            t=p[i].first;
        }

    }
    cout<<res<<endl;
}

int main()
{
    while(cin>>n)
    {
        for(int i=0;i<n;i++)
        {
            cin>>start[i]>>myend[i];
        }

        solve();
    }

    return 0;
}

 

 2.2.3 字典序最小问题

 

 

 

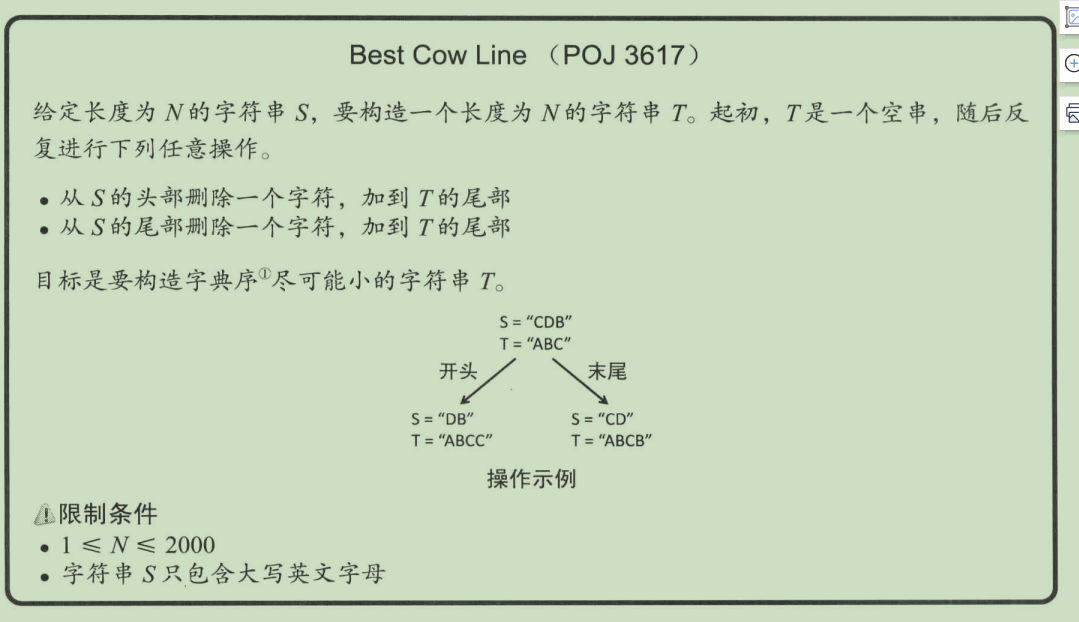
我们很容易想出    让s的首部与s的尾部进行比较  哪个小选那个

　　　　　　　　不过对于s的首部和尾部字母相同时，我们需注意，此时应进行首下一个字母的比较 然后选择字典序较小的

 

#include<iostream>
using namespace std;
int n;
const int MAX=2e3;
char arr[MAX+1];

void solve()
{
    int count=0;
　　　　//a代表首部    b代表尾部
    int a=0,b=n-1;
    while(a<=b)
    {
         bool left=false;
        //i 表示到左右两端的距离
　　　　//逐一比较 确定选择首部还是尾部

        for(int i=0;a+i<=b;i++)
        {
            if(arr[a+i]<arr[b-i])
            {
                left=true;
                break;
            }else if(arr[a+i]>arr[b-i])
            {
                left=false;
                break;
            }
        }

        if(left)putchar(arr[a++]);
        else putchar(arr[b--]);

        count++;
        if(count%80==0)putchar('\n');
    
    }
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)cin>>arr[i];

    solve();
    return 0;
}

 2.2.4 其他问题

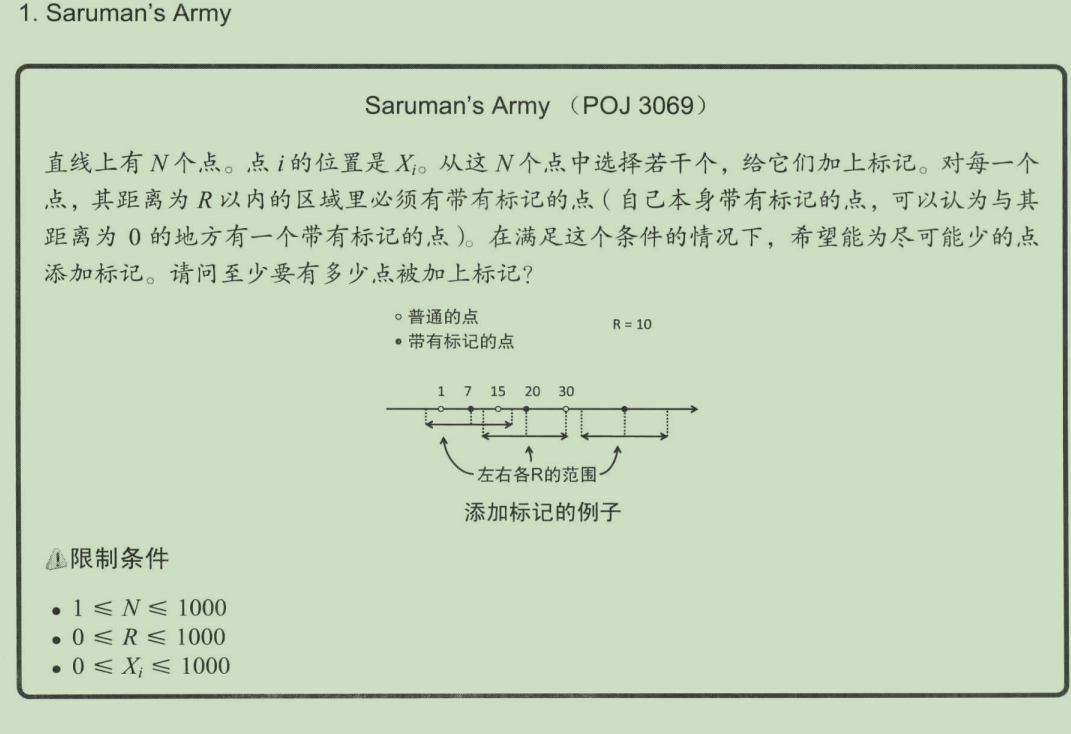
1.Saruman's  Army

 

 

 

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
int r,n;
const int MAX=1e3;
int arr[MAX];

void solve()
{
    int ans=0;
    sort(arr,arr+n);//为了能够从最左侧看起

    //定义左侧标记
    int i=0;
    while(i<n)
    {
        //定义未被覆盖的最左侧的位置
        int s=arr[i++];
        //向右前进到arr[i]>s+r
        while(i<n&&arr[i]<=s+r) i++;
        //p是新的标记位置
        int p=arr[i-1];
        //再次前进到未被覆盖的最左侧的位置
        while(i<n&&arr[i]<=p+r)i++;

        ans++;
    }
    cout<<ans<<endl;
}

int main()
{
    while(cin>>r>>n)
    {
        if(r==-1&&n==-1){break;}

        for(int i=0;i<n;i++)cin>>arr[i];

        solve();
    }
    return 0;
}

 

2. Fence Repair　　　　　　　 

 

本质而言  构造最小生成树  即可

#include<iostream>
using namespace std;
int n;
const int MAX=2e4+5;
int arr[MAX];


void solve()
{
    long long ans=0,temp=0;
    
    // int L=n;
    while(n>1)
    {

　　　　　　//我们不必排序(O(n*logn))   就单纯的找两个变量 不断的更改就行(O(n))

int min1=0,min2=1;
        if(arr[min1]>arr[min2])swap(min1,min2);
        //遍历数组  使最小min1  最大min2
        for(int i=2;i<n;i++)
        {
            if(arr[i]<arr[min1])
            {
                min2=min1;
                min1=i;
            }else if(arr[i]<arr[min2])
            {
                min2=i;
            }
        }

        //拼接节点
        temp=arr[min1]+arr[min2];
        ans+=temp;

        //把temp填入数组  并把arr[n-1]的位置用于取消掉  
        //用min1来填入temp  min2把原来的arr[n-1]位置的数记录
        if(min1==n-1)swap(min1,min2);

        arr[min1]=temp;
        arr[min2]=arr[n-1];
        n--;
        
        // L--;
    }
   
   cout<<ans;


}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)cin>>arr[i];

    solve();
    return 0;
}