第二天 第2.1节

2.1最基础的穷竭搜索

2.1.1递归函数

对于斐波那契数列：

 

 

 

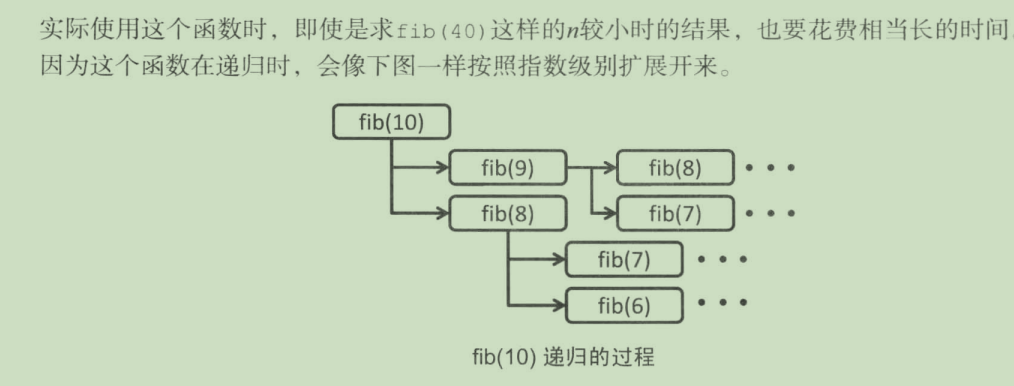
 显然中间重复调用了许多fib(n)

因此，为什么不准备一个数组存放 fib(n) ?

显然，这样可以大大提高speed

 

 

 2.1.2栈

先进后出

 

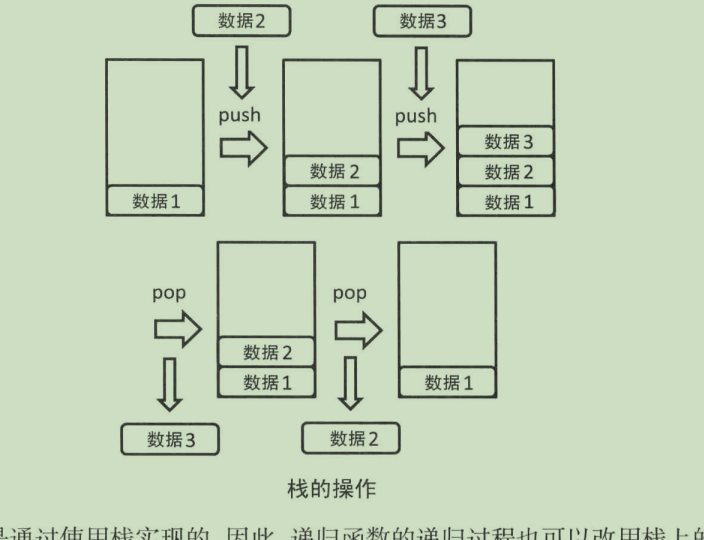
 函数调用的过程其实是通过栈来实现的      /*（汇编语言）*/

 

 2.1.3队列

先进先出

 

 

 

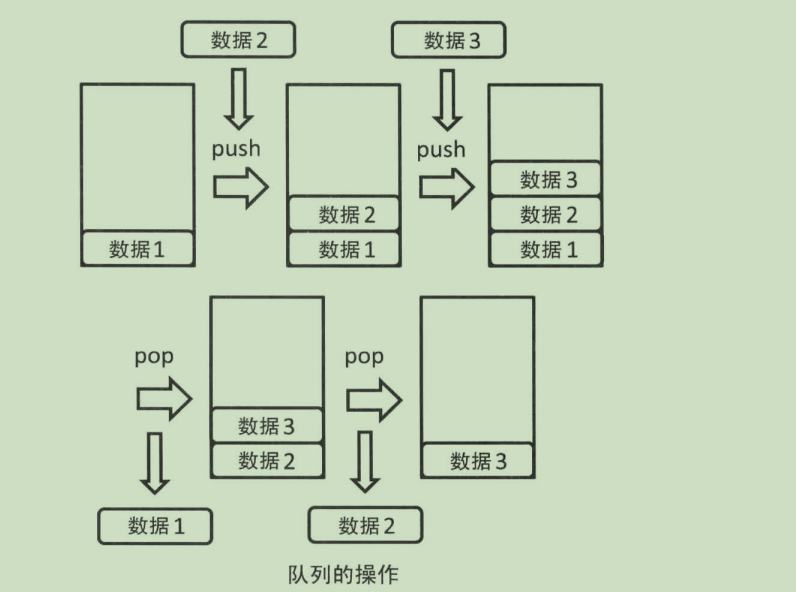
 2.1.4深度优先搜索DFS

Depth-First Search

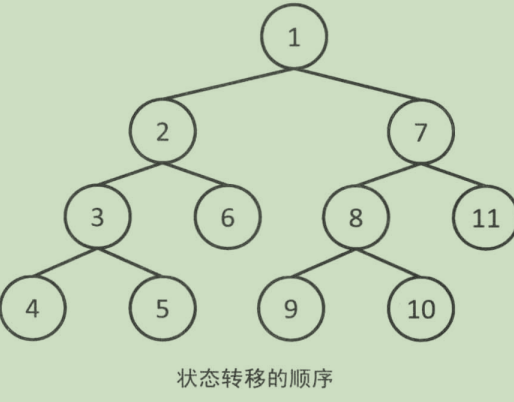
它从某个状态开始，不断地转移状态，直至无法转移；

然后便退回到上一步的状态，继续重复操作。

如此不断重复，直至找到最终的解。

用递归函数实现比较简单

 

 

部分和问题

 

#include<iostream>
using namespace std;
int n,k;
const int MAX=20;
int arr[MAX];

//i表示状态： 已经选了i-1个数  正在进行第i个数的选择
//sum表示已选择i-1个数的和
bool dfs(int i,int sum)
{
    //4                    0-3
    //1 2 4 7
    //13
    //递归中止条件
    if(i==n-1)
    {
       if((sum+arr[i]==k)||sum==k)
       {
           return true;
       }
       return false;
    }
    //选i    这里一定要注意直接调用dfs(不会给本身的dfs返回值)    dfs(i+1,sum+arr[i])
    if(dfs(i+1,sum+arr[i]))return true;

    //不选i
    if(dfs(i+1,sum))return true;
    return false;
}

void solve()
{
    if(dfs(0,0))
    {
        cout<<"Yes"<<endl;
    }else
    {
        cout<<"No"<<endl;
    }
}

int main()
{
    while(cin>>n)
    {
        for(int i=0;i<n;i++)cin>>arr[i];

        cin>>k;

        solve();

    }
    return 0;
}

 

 水洼计数

#include<iostream>
using namespace std;
int n,m;
const int MAX=105;
char arr[MAX][MAX];

//i j 表示第i j 处水洼  
//在dfs中将向四周搜寻其有没有连通的水洼
//如果有再接着dfs直至没有
void dfs(int i,int j)
{
    //向八个方向
    for(int dx=-1;dx<=1;dx++)
    {
        for(int dy=-1;dy<=1;dy++)
        {
            //当前位置
            int nx=i+dx,ny=j+dy;
            if(nx>=0&&nx<n&&ny>=0&&ny<m&&arr[nx][ny]=='W')
            {
                //先将此处水洼变为.  再次搜寻此处水洼的四周
                arr[nx][ny]='.';
                dfs(nx,ny);
            }
        }
    }
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
        cin>>arr[i];

    //水洼总数
    int res=0;
    //首先找到第一处水洼
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            if(arr[i][j]=='W')
            {
                //现将此处水洼标记未.  res++
                //再dfs其四周
                arr[i][j]='.';
                res++;
                dfs(i,j);
            }
        }
    }
    cout<<res;
    return 0;
}

 

 

 

 2.1.5宽度优先搜索BFS

Breadth-First Search（哈哈   width breadth  宽度   而bread是面包）

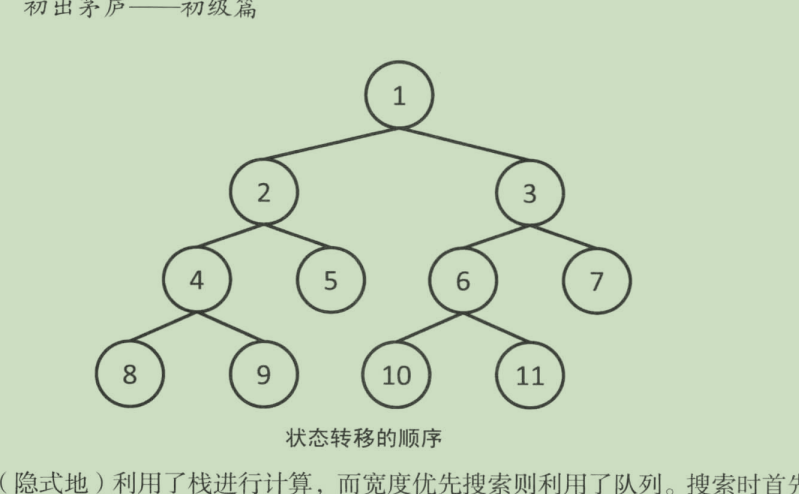
与DFS不同之处在于搜索的顺序   DFS是当前状态不能再进行转移时回复到上一个状态

而BFS总是优先搜索距离初始状态近的状态

 

深度优先搜索隐式的利用了栈来进行计算

而宽度优先搜索则利用了队列

 迷宫的最短路径 

 

 解决方案 O(N*M)

 

#include<iostream>
#include<queue>
using namespace std;

int n, m;
const int MAX = 105;
char arr[MAX][MAX];
typedef pair<int, int> P;

int dx[4] = { 0,0,-1,1 };//上下左右
int dy[4] = { -1,1,0,0 };
int sx, sy, gx, gy;
int d[MAX][MAX];
const int INF = 100000000;
  
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)cin >> arr[i];

    //找起点终点坐标
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            if (arr[i][j] == 'S')
            {
                sx = i, sy = j;
            }
             if (arr[i][j] == 'G')
            {
                gx = i, gy = j;
            }
        }
    }
    queue<P> que;
    //将起点坐标添加到队列
    que.push(P(sx, sy));
    //把到各个地方的最短距离设置为无穷大  并把到起点的距离设置为0
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            d[i][j] = INF;
        }
    }

    d[sx][sy] = 0;
    while (!que.empty())
    {
        P p = que.front();
        que.pop();
        //如果取出的就是终点则直接输出就行
        if(p.first==gx&&p.second==gy)
        {
           break;
        }

        for (int i = 0; i < 4; i++)
        {
            //当前位置
            int nx = p.first + dx[i], ny = p.second + dy[i];
            //如果当前位置可以走(是否越界 是否为. 是否已经访问过 若访问过则此次绝对不是最短距)  则加入队列
            //如果不可以走就算了
            //千万注意边界的处理  此处一定要注意判断是否在边界内（坑了几个小时！！！）
            if (nx >= 0 && nx < n && ny>=0 && ny < m && arr[nx][ny] != '#' && d[nx][ny] == INF)
            {
                que.push(P(nx, ny));
                //并且距离加一
                d[nx][ny] = d[p.first][p.second] + 1;
            } 
        }

    }

            cout<<d[gx][gy];
            return 0;

}