第一天 第一章

第一章

时间复杂度估算  

报错须知

 1.抽签

问题描述

一个袋子中有 n 个数字纸片，每张上面都写了一个数字。

我们有 4 次机会，每次从袋子中选一个纸片，记录下数字，然后放回去（因此一个纸片可能多次被选中）。

当存在一个可能，使得 4 张纸片的数字总和等于 m，则输出 Yes，否则输出 No

解决方案：  O(n*4)   O(n*3logn)  O(n*2logn)

当我们将四个数看作看 k1+k2+k3=m-k4时：
可以先三重循环枚举k1+k2+k3  然后在排好序的数组中二分搜索 m-k1-k2-k3 
看其是否存在即可

//O(n*3logn)
#include<iostream>
using namespace std;
#include<algorithm>
//准备 数组arr  n  m
const int MAX=100;
int arr[MAX];
int n,m;

bool search(int target)
{
    int l=0,r=n-1;
    while(l<r)
    {
        int mid=(l+r)/2;
        if(arr[mid]<target)
        {
            l=mid+1;
        }else if(arr[mid]==target)
        {
            return true;
        }
        else 
        {
            r=mid-1;
        }
    }
    return false;
}

int main()
{   
　　//输入
    cin>>n>>m; 
    for(int i=0;i<n;i++)
    {
        cin>>arr[i];
    }

    bool flag=false;
　　//排序
    sort(arr,arr+n);
　　//枚举
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            for(int k=0;k<n;k++)
            {
　　　　　　　　　　//二分搜索
                if(search(m-arr[i]-arr[j]-arr[k]))
                {
                    flag=true; 
                }
            }
        }
    }

    if(flag)
    {
        cout<<"Yes";
    }else{
       cout<<"No"; 
    }

    return 0;
}

 

 

而当我们看作 k1+k2=m-k3+k4时：

也就是我们可以先将抽两次签的情况枚举并保存在一个数组arr1中

然后排序  再枚举k3+k4  观察能否在arr1中二分搜索到m-k3-k4

 #include<iostreamusing namespace std;#include<algorithm>

//准备n ，m arr arr1
int n,m;
const int MAX=1000;
int arr[MAX];
int arr1[MAX*MAX];

bool search(int target)
{
    int l=0,r=n*n-1;
    int mid;
    while(l<=r)
    {
        mid=l+((r-l)>>1);
        if(arr1[mid]==target)
        {
            return true;
        }else if(arr1[mid]>target)
        {
            r=mid-1;
        }else
        {
            l=mid+1;
        }
    }
    return false;
}

void solve()
{
　　//枚举抽两次并用arr1保存
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        arr1[i*n+j]=arr[i]+arr[j];

　　//二分搜索前先排序
    sort(arr1,arr1+n*n);
　　//枚举k3+k4
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++if(search(m-arr[i]-arr[j]))
            {
                 cout<<"Yes";
                 return;
            }
        }
    }
    cout<<"No";
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>arr[i];
    solve();
    return 0;
}

 

2.三角形

问题描述

有 n根棍子，棍子 i 的长度为 a_i 。想要从中选出 3 根棍子组成周长尽可能长的三角形。

请输出最大的周长，若无法组成三角形则输出 0。

 解决方案  O（n*3）    O(nlogn)

假若我们将数组排好序，从大的往小的方向看：

如果arr【k】<arr【k-1】+arr【k-2】即两较小的边之和大于第三边  则就是最大的三角形

否则k-- （因为arr【k-1】，arr【k-2】已经是除了arr【k】之外最大的数了，所以arr【k】不可能构成三角形）

就这样从大到小考虑每条边

#include<iostream>
using namespace std;
#include<algorithm>
const int MAX=105;
int n;
int arr[MAX];
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)cin>>arr[i];


    sort(arr,arr+n);
    for(int i=n-1;i>=2;i--)
    {
        if(arr[i]<(arr[i-1]+arr[i-2]))
        {
            cout<<arr[i]+arr[i-1]+arr[i-2];
            return 0;
        }
    }

    cout<<0;
    return 0;
}

 

3.蚂蚁

问题描述

 

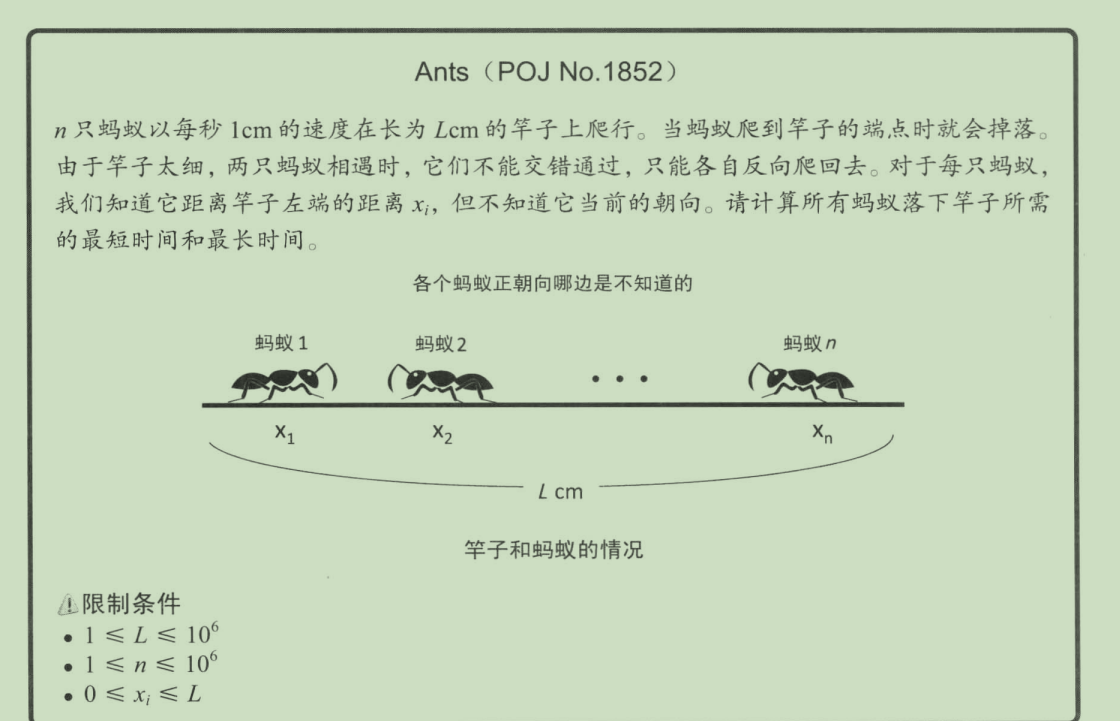
 解决方案   O（n）

我们考虑当两只蚂蚁碰撞时，两蚂蚁各自掉头（但蚂蚁完全相同，可看作没有掉头啊）

所以对于一只蚂蚁而言 其最短离开杆子时间时min（x，L-x），最长时间 max(x，L-x)

因此所有蚂蚁下杆的最短时间便是 最后一只蚂蚁离开的最短时间    即所有蚂蚁离开的最短时间的最大值

　　所有蚂蚁下杆的最长时间便是  最后一只蚂蚁离开的最长时间   即所有蚂蚁离开的最长时间的最大值

//此程序针对多组输入处理
#include<iostream>
using namespace std;
#include<algorithm>
int t;
int l,n;
const int MAX=1e6;
int arr[MAX];
int main()
{
    cin>>t;
    while(t--)
    {
　　　　//这里对每一组输入数据进行处理
        cin>>l>>n;
        for(int i=0;i<n;i++)
        {
            cin>>arr[i];
        } 
　　　　//最短时间  最长时间
        int minT=0,maxT=0;
　　　　//最短时间： 所有蚂蚁离开的最短时间的最大值
        for(int i=0;i<n;i++)
        {
            minT=max(minT,min(arr[i],l-arr[i]));
        }
　　　　//最长时间： 所有蚂蚁离开的最长时间的最大值
        for(int i=0;i<n;i++)
        {
            maxT=max(maxT,max(arr[i],l-arr[i]));
        }
        cout<<minT<<" "<<maxT<<endl;

    }

    return 0;
}