03-1 模式设计

关系模式设计的问题

• 数据冗余
• 更新异常
• 插入异常
• 删除异常

为了解决这些问题，应采用模式分解的方式

关系模式分解

模式分解定义：\(R(U)\) 分解为 \(R1(U1),...,Rk(Uk)\)，\(R1,...,Rk\) 称为一个分解

模式分解包括：

• 属性集的分解
• 函数依赖集的分解
  • \(R(A, B, C)\), \(F=\{A→B, C→B\}\), 则分解为 \(R_1 (A,B)\), \(R_2(A,C)\) 丢失了 \(C→B\)

模式分解标准

• 具有无损连接：数据不丢失
• 要保持函数依赖：

无损连接

将关系模式 \(R\) 分解为 \(R1,...,Rk\)

\[m_{\rho}(r)=\infty_{i=1}^{k}\pi_{Ri}(r) \]

无损连接要求 \(r = m_{\rho}(r)\)

无损连接保证 R 分解后还可以通过 Ri 恢复
R 的每个关系 r 是它在 Ri 上的投影的自然连接

测试方法：

1. 分解成两个的情况

\(p = \{R1,R2\}\)，满足条件之一：

\[\begin{align*} (R1\cap R2)\rightarrow(R1-R2)\\ (R1\cap R2)\rightarrow(R2-R1) \end{align*} \]

p 为无损连接。

2. 分解成多个的情况

Chase 方法

保持函数依赖

关系模式的范式

1NF：数据库表的每一列都是不可分割的基本数据项，同一列中不能有多个值，即实体中的某个属性不能有多个值或者不能有重复的属性。

2NF：\(R\in 1NF\)，且每个非主属性完全依赖于任何一个主码。(不能局部依赖)

• 完全函数依赖：对于函数依赖 W→A，若不存在 \(X⊂W\)，并且 X→A 成立，则称 W→A 为完全函数依赖，否则为局部函数依赖

R(A,B,C,D,E), {A,B}为主码

• AB→C， AB→D， AB→E
• A→C、 B→C、 A→D、 B→D、 A→E、B→E中任何一个均不成立

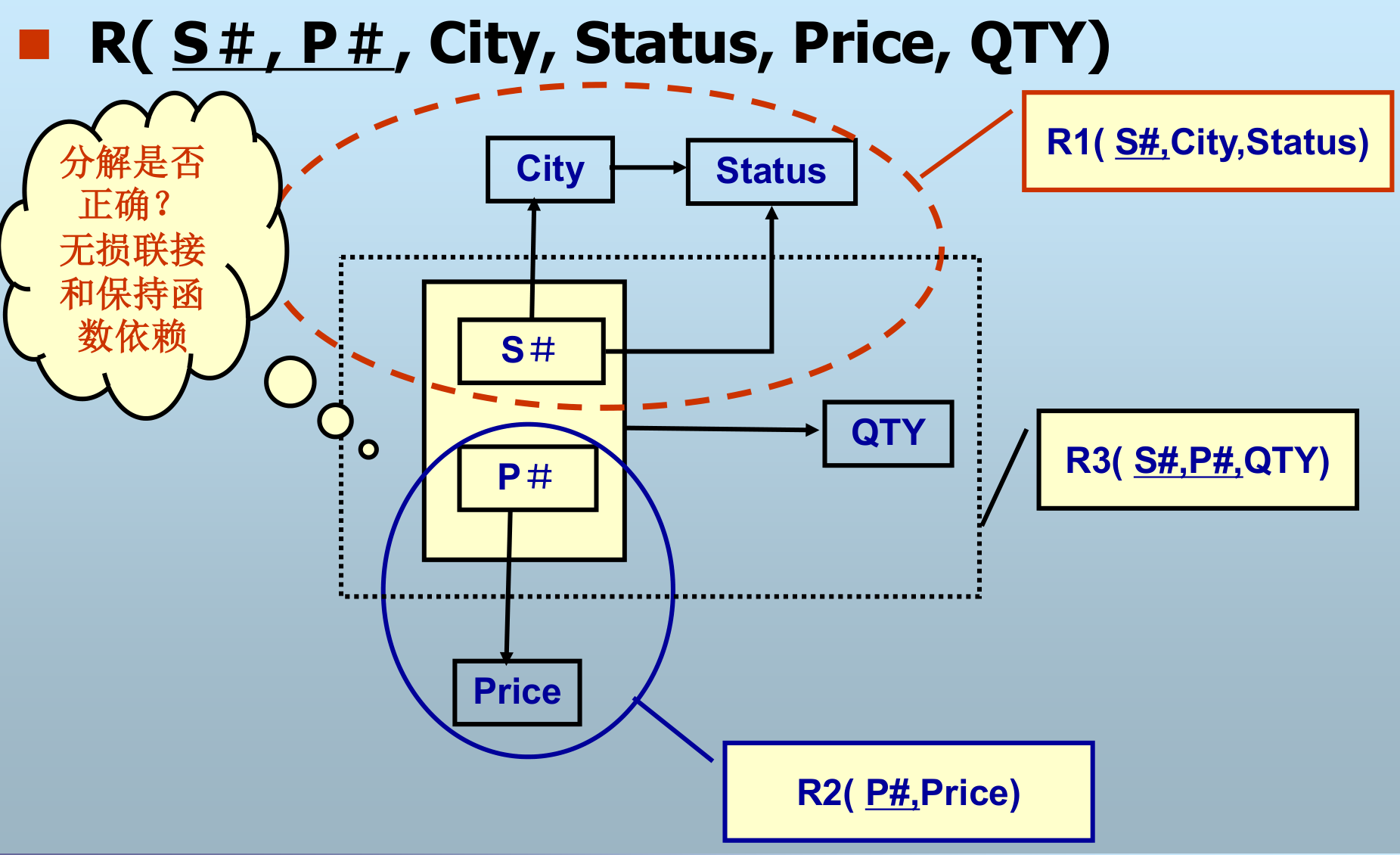
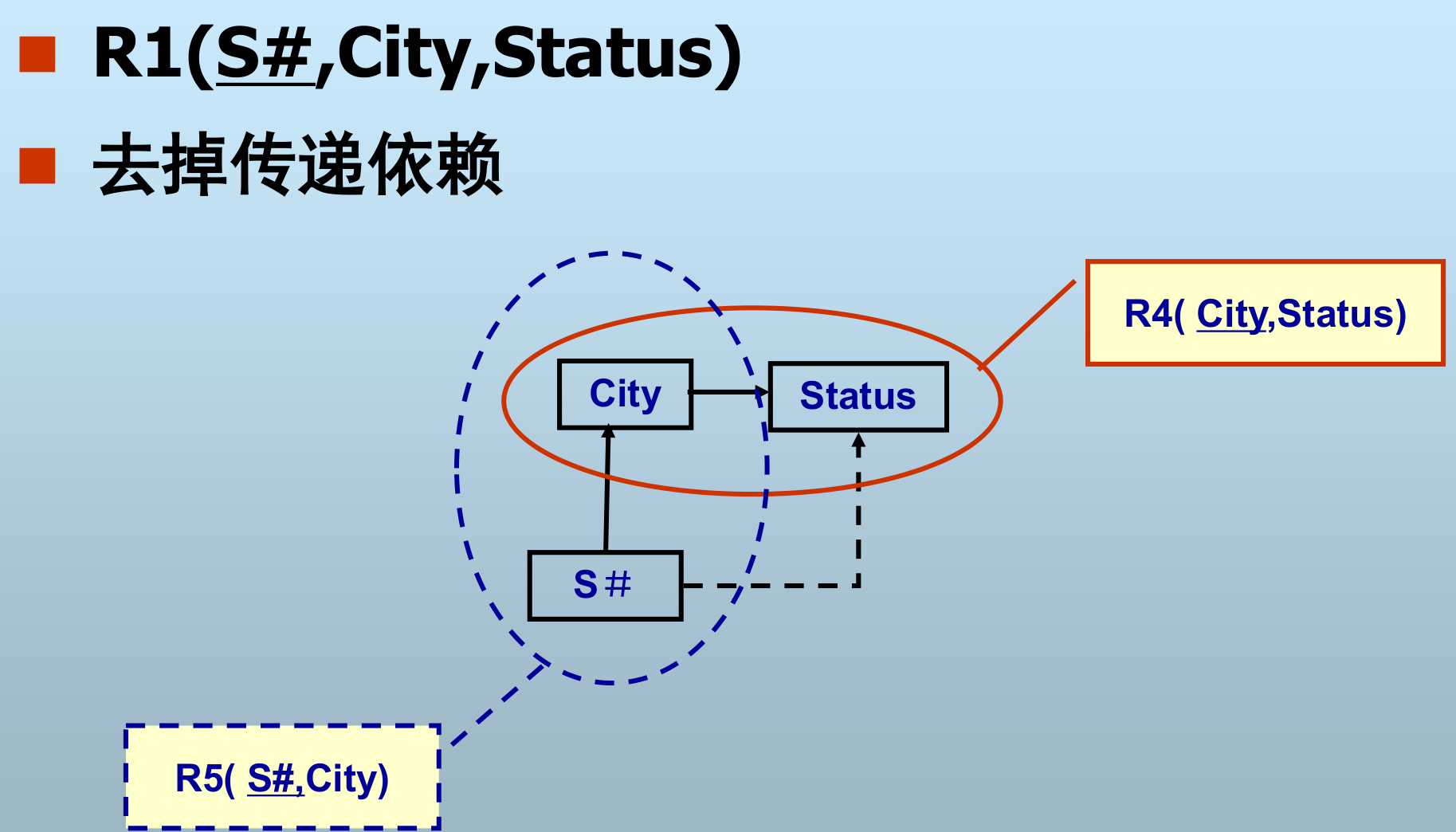
3NF：\(R<U,F>\in2NF\)，非主属性且不传递依赖于码。

• 传递依赖：若 Y→X，X→A，并且 \(X\nrightarrow Y\)，A 不是 X 的子集，则称 A 传递依赖于 Y

BCNF：所有函数依赖左端都必须是候选码

• BCNF 扩充了 3 NF，可以处理 R 有多个候选码的情形
• BCNF：如果关系模式 R 的所有不平凡的、完全的函数依赖的决定因素（左边的属性集）都是候选码，则 R∈BCNF
• 不一定能保持函数依赖，需要删除左边非超码的 FD

{SNAME, P#} →QTY,{S#, P#} →QTY,S# →SNAME, SNAME →S#
{SNAME, P#} 和 {S#, P#} 都可以是候选码

模式分解的算法

保持函数依赖地分解到 3 NF 的算法

1. 求最小函数依赖集
2. 去除不在 F 中出现的属性，这些属性组成关系模式记为 \(R'\)
3. 如果 F 存在 \(X\rightarrow A\) 且 \(XA=U\) 则最后输出结果为 \(R(U),R'\)。否则
4. 对 F 按照左部分分组，将每组涉及的所有属性作为一个关系模式输出。如果某个关系模式 \(Ri\) 的属性集是另一个关系模式的属性集的子集，则在结果中去掉 \(Ri\) 。最后输出 \(p=\{R1,R2,...,Rk,R'\}\)

找到函数依赖的涉及的所有属性构成一个表，表有包含则去除

无损并且保持函数依赖分解为 3 NF 的算法

1. 用算法 1 求出 R 的保持函数依赖的 3NF 分解。得到 \(q=\{R1,...,Rk\}\)
2. X 是 R 的主码，求出 \(p=q\cup{R(X)}\)
3. 若 X 是 q 中某个 Ri 的子集，则在 p 中去掉 R (X)。

说白了就是再加一个包含主码的关系，如果重复了就去除

例子 1：

例子 2：

无损分解为 BCNF 的算法

1. \(p=\{R\}\)
2. 检查是否满足 BCNF
3. 关系模式中存在 \(X\rightarrow A\)，X 不是超码
   1. 分解为 \(S1 (XA),S2(U-A)\)
   2. \(p={p-S}\cup{S1,S2}\)
   3. 回到 2 再次检查

找到左边不是超码（注意是超码）的函数依赖，将涉及的属性组成一个关系，右边的属性从原关系删除。重复直到满足 BCNF