02 关系数据库

数据库体系结构 (模式)

ANSI/SPARC 体系结构——三级模式结构＋两级映象

数据库模式的概念

  • 模式（Schema）

    • 数据库逻辑结构和特征的描述
    • 仅仅涉及类型的描述，不涉及具体的值
    • 反映的是数据的结构及其联系
    • 模式是相对稳定的

  • 实例（Instance）

    • 模式的一个具体值
    • 反映数据库某一时刻的状态
    • 同一个模式可以有很多实例
    • 实例随数据库中的数据的更新而变动

模式：

学生表 (学号，姓名，年龄)
课程表 (课程号，课程名，学分)
选课表 (学号，课程号，成绩)

数据库三级模式结构

ANSI/SPARC 体系结构——三级模式结构＋两级映象

Oracle、Informix 等 SQL 数据库系统的模式结构可通过 ANSI/SPARC 体系结构进行解释

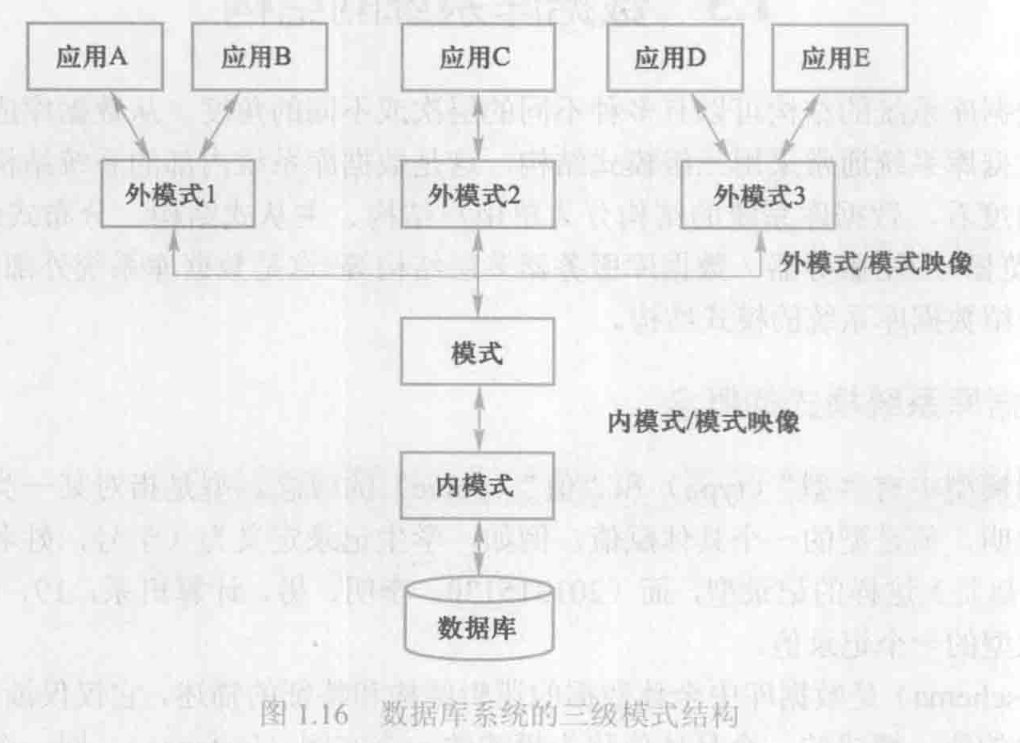
概念模式（模式、逻辑模式）（Schema）

  • 数据库中全体数据的逻辑结构和特征的描述。
    • 数据记录由哪些数据项构成
    • 数据项的名字、类型、取值范围
    • 数据之间的联系、数据的完整性等
  • 一个数据库只能有一个概念模式
  • 概念视图是概念模式的实例
  • 所有用户的公共数据视图。

通过模式 DDL 定义模式

外模式（子模式，用户模式）（External Schema）

  • 单个用户使用的局部数据的逻辑结构和特征的描述。
  • 对于用户而言，外模式就是数据库
  • 建立在概念模式之上，同一模式上可有多个不同的外模式
  • 外部视图是外模式的实例
  • 数据库用户的数据视图，是与某一应用有关的数据的逻辑表示。

通过子模式 DDL 定义外模式

内模式（存储模式）（Internal Schema）

  • 是数据物理结构和存储方式的描述。
    • 记录的存储方式（例如，顺序存储，按照 B 树结构存储，按 hash 方法存储等）。
    • 索引的组织方式：排序/散列
    • 数据是否加密，数据是否压缩存储。
  • 不涉及物理块（或页）的大小，也不考虑具体设备的柱面或磁道大小
  • 一个数据库只有一个内模式
  • 是数据在数据库内部的表示方式。
  • 内部视图是内模式的实例
  • 数据存储记录结构的规定。

通过内模式 DDL 定义内模式

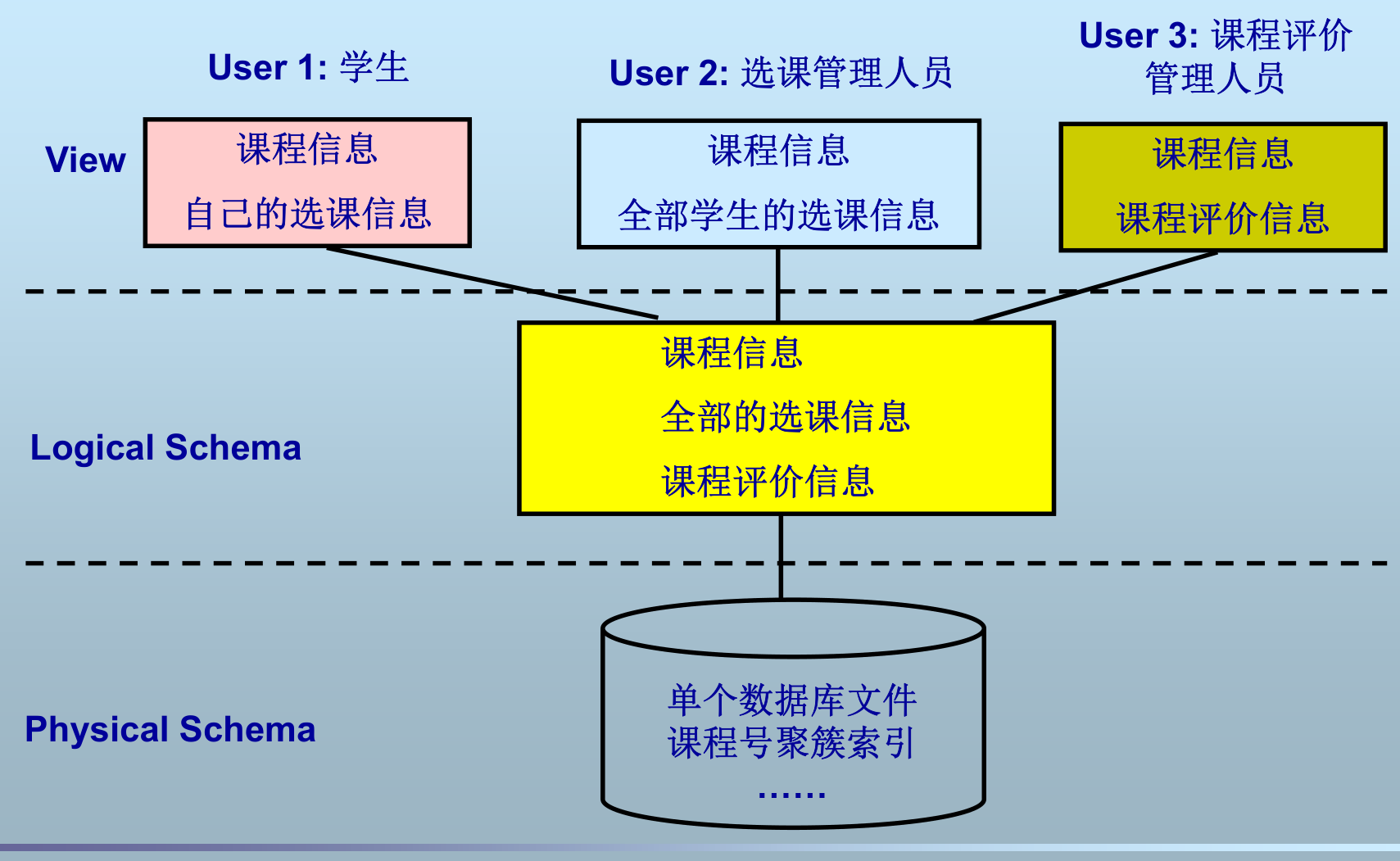
二级映象和数据独立性

外模式／模式映像

  • 定义了外模式与概念模式之间的对应关系
    • 同个属性在外模式和模式中的名称可能不同。
    • 外模式中的属性可能由模式中的多个属性运算而得
  • 当模式改变时，数据库管理员对外模式／模式映象作相应改变，使外模式保持不变。
  • 保证数据的逻辑独立性。
    • 应用程序是依据数据的外模式编写的，应用程序不必修改，保证了数据与程序的逻辑独立性，简称数据的逻辑独立性。

模式／内模式映像

  • 定义了概念模式与内模式之间的对应关系
    • 概念模式中的逻辑记录和字段在内部如何表示
  • 当数据库的存储结构改变了（例如选用了另一种存储结构），数据库管理员修改模式／内模式映象，使模式保持不变。
  • 保证数据的物理独立性。
    • 应用程序不受影响。保证了数据与程序的物理独立性，简称数据的物理独立性。

体系结构

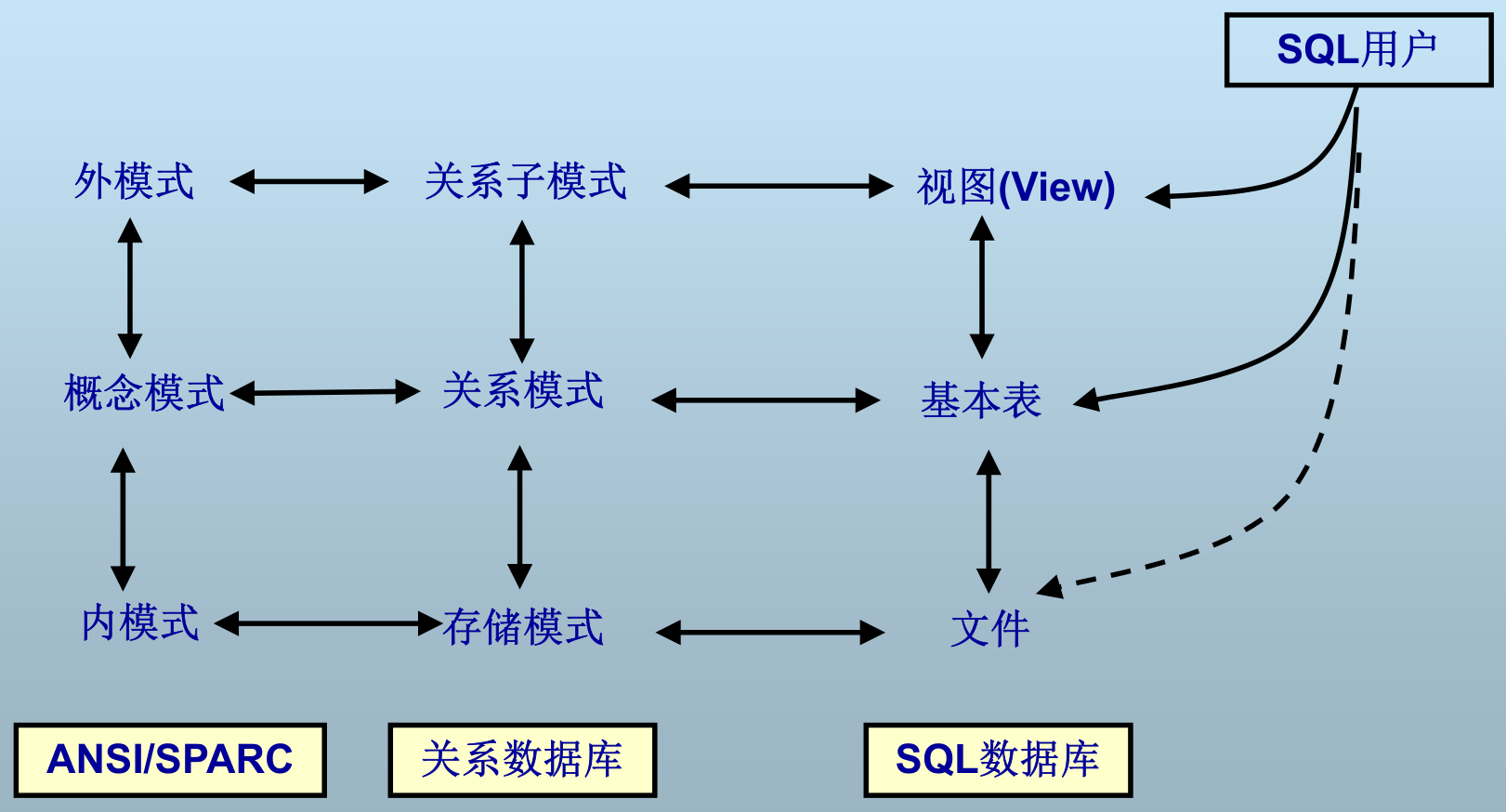
关系数据模型

定义：描述现实世界实体、实体间联系以及数据语义和一致性约束的模型

分类：

  1. 概念数据模型（概念模型）
    • 按用户的观点对数据进行建模，强调语义表达功能
    • 独立于计算机系统和 DBMS
    • 主要用于数据库的概念设计
  2. 结构数据模型（数据模型）
    • 按计算机系统的观点对数据进行建模，直接面向数据库的逻辑结构
    • 与计算机系统和 DBMS 相关
    • 有严格的形式化定义，以便于在计算机系统中实现

数据抽象层次：

flowchart LR 现实世界 --> 概念模型 --> 数据模型

数据模型要素

  • 数据结构：现实世界实体及实体间联系的表示和实现
  • 数据操作：数据检索和更新的实现
  • 数据的完整性约束：数据及数据间联系应具有的制约和依赖规则

关系模型

用规范化的二维表格结构表示实体集，外码表示实体间联系，三类完整性表示数据约束的数据模型

关系模式

  • 关系模式（Relation Schema）
    • 关系的逻辑结构和特征的描述
    • 对应于二维表格的表头
    • 通常由属性集和各属性域表示，不关心域时可省略域
  • 关系：关系模式的实例，即二维表（元组的集合）
  • 关系数据库模式（Relational DatabaseSchema）：关系模式的集合
  • 关系数据库：关系数据库模式的实例

关系模式可以形式化定义：\(R(U,D,dom,F)\)。

  • U 是一个属性集
  • D 是 U 中属性的值所来自的域
  • Dom 是属性向域的映射集合
  • F 是属性间的依赖关系，在实际中一般只考虑函数依赖

函数依赖

函数依赖定义：一个关系模式中一个属性集和另一个属性集间的多对一关系

  • 形式化定义：有关系模式 \(R(U)\)，\(X,Y\) 是 \(U\) 的子集。若两元组 \(t_{1},t_{2}\) ，由 \(t_{1}[X]=t_{2}[X]\) 导致 \(t_{1}[Y]=t_{2}[Y]\) 则 Y 函数依赖于 X，\(X\rightarrow Y\)

例如有选课关系SC(S#, C#, Score)
存在由属性集{S#, C#}到属性集{Score}的函数依赖：

  • 对于任意给定的S#值和C#值，只有一个Score值与其对应
  • 反过来，可以存在多个S#值和C#值，它们对应的Score值相等

逻辑蕴含：设 F 是关系模式 R 的一个函数依赖集，X 和 Y 是 R 的属性子集，若从 F 的函数依赖中能推出 X→Y，则称 F 逻辑蕴含 X→Y

函数依赖集的闭包：函数依赖集 F 逻辑蕴含的函数依赖的全体构成的集合称为 F 的闭包

Armstrong 公理：

属性集的闭包：设 F 是属性集 U 上的一个 FD 集，X 是 U 的子集，则称所有用 Armstrong 推理规则推出的函数依赖 X→A 中所有 A 的集合，称为属性集 X 关于 F 的闭包，记做 X+

最小函数依赖集

  • F 的每个 FD 的右边只有一个属性
  • F 不可约
  • F 的每个 FD 的左部不可约

求解过程：

  1. 右边都写成单属性，然后去重
  2. 消除左部冗余属性，然后去重
  3. 消除冗余函数依赖

关系代数

选择（选取行）

  • R 关系
  • F 条件

投影 （选取列，可能会删除部分行避免重复）

  • A 属性列

连接

  • A, B 属性组
  • \(\theta\) 比较关系
  • 从笛卡尔积 \(R\times S\) 中选择 A，B 属性组满足比较关系 \(\theta\) 的运算的元组
  • 常用连接
    • 等值连接： \(\theta\) 为 \(=\)
  • 自然连接：一种特殊的等值连接，在结果中删除重复的属性列
posted @ 2024-01-17 13:01  ConnorLan  阅读(39)  评论(0)    收藏  举报