除法查找表生成推导matlab

1.1 除法查找表生成推导

假设查找表位宽为rom_bit，那其能表示的范围是 0~2^{𝑟𝑜𝑚_𝑏𝑖𝑡}−1；假设 leading位数为 leading_bit，范围是 2^{leading_bit−1}~2^leading_bit−1，因为最高位恒为 1，那查找表入口地址位宽为 𝑎𝑑𝑑𝑟_𝑏𝑖𝑡=𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡−1。其地址能表示的范围是 0~2^{𝑎𝑑𝑑𝑟_𝑏𝑖𝑡}−1，实际对应的值为 1 / (2^leading_bit−1)~1 / (2^{leading_bit−1})。要将实际值和查找表所能表示的最大值对应上，则查找表输出值对应实际值相差 2^𝑥倍，则有 2^{𝑟𝑜𝑚_𝑏𝑖𝑡}−1=2^𝑥x1/(2^{leading_bit−1})，差 1忽略 ,则有 𝑥=𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡−1+𝑟𝑜𝑚_𝑏𝑖𝑡=𝑎𝑑𝑑𝑟_𝑏𝑖𝑡+𝑟𝑜𝑚_𝑏𝑖𝑡。
考虑到leading位查找表每次都舍弃 leading位后面的值，整体计算结果会偏大，考虑取 leading位能够包含所有数的中间值作为查找表的值。

例如， 24位二进制数1000_0001_0000_0000_0000_0000_0000_0000，拟取 8位 leading位 1000_0001，该 leading位能够涵盖的所有值的范围包括如下范围：

1000_0001_0000_0000_0000_0000_0000_0000~1000_0001_1111_1111_1111_1111_1111_1，取中间值 1000_0001_1000_0000_0000_0000_0000_0000，即取 leading位后第一位为 1
其余位为 0，参与计算查找表的值。（没有采用，因为截位的时候会偏小，和查表偏大近似抵消）。

1.1.1 查找表的制定

查找表的制定主要是两个参数：

       查找表的地址宽度：由leading长度决定，leading长度-1；

       查找表的数据宽度：由误差决定。

这两个参数主要是通过计算该两个参数对查表误差的影响来进行确定。。

这里以leading位为8位，查找表地址宽度为7位、查找表的数据宽度位9位，即addr_bit=7，leading_bit=8，rom_bit=9为例进行讲解：

1、除数值的处理

前述提到除法可以转化为与倒数的乘法，因此主要是将除数的倒数的值计算出来并存储到查找表相应位置。由于leading位取的是非零最高位，因此在截位之后的leading_bit的值最高位一定为1，即为8’b1xxxxxxx。因此除数的值范围为 2^{leading_bit−1}~2^leading_bit−1，即128~255，其倒数的值为 1 / (2^leading_bit−1)=1/255~1 / (2^{leading_bit−1})=1/128 ，其中1 / (2^{leading_bit−1}) = 1/128 为最大值。为了防止查找表的浪费，将查找表的地址位宽addr_bit取leading_bit-1，即7位。

这样的话，可以将 0~2^addr_bit−1(0~127)地址与1 / (2^leading_bit−1)=1/255~1 / (2^{leading_bit−1})=1/128 相对应。0对应1 / (2^{leading_bit−1})=1/128 ，1对应1 / (2^{leading_bit-1}+1)=1/(128+1)应 ，addr对应1 / (2^{leading_bit-1}+addr) 。

2、查找表中的值

由于除数倒数为  1 / (2^leading_bit−1)=1/255~1 / (2^{leading_bit−1})=1/128，但是由于是浮点小数，并不知道它的位宽。因此需要将所有浮点小数中的最大值 1 / (2^{leading_bit−1})=1/128扩展到2^rom_bit−1 ，即 1 / (2^{leading_bit−1})乘2^{𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡−1+𝑟𝑜𝑚_𝑏𝑖𝑡} =2^rom_bit ，但是由于查找表位宽为rom_bit，最大值为2^rom_bit -1，将会溢出，因此在地址为0的时候，取查找表的值之后需要减去1。其余查找表的值与地址的关系相对应：

rom(addr) = 2^{𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡−1+𝑟𝑜𝑚_𝑏𝑖𝑡} / (2^{leading_bit-1}+addr) 

rom(0) =[ 2^{𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡−1+𝑟𝑜𝑚_𝑏𝑖𝑡} / (2^{leading_bit-1}) ]-1 

1.1.2 除法的估算（查表操作）

在得到了查找表之后，根据查找表即可实现除法运算，具体步骤如下：

 

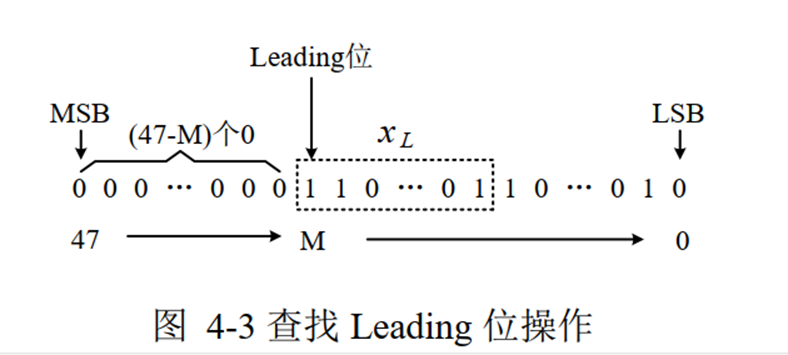
1、计算leading位

由于采用的找leading位的方式位找非零最高位，因此leading位为floor(log2(x))（从0开始计），令M= floor(log2(x))。

2、截位

由于leading为M，leading_bit为8，因此需要截M+1-leading_bit位，即截M-7位。此时需要除以2^{M+1−leading_bit}，即 2^M−7 。但是因为最高位都为1省略了，因此需要减去2^leading_bit ，即减去 2⁷，此时的值即为 ，此时的值即为查找表的地址（matlab中需要加1）。

addr=floor(x/2^{M−leading_bit}) − 2^{M−leading_bit}

 

3、查表

将前述算出来的地址进行查表得到相应的值，即

 rom(addr)=rom(floor(x/2^{M−leading_bit}) − 2^{M−leading_bit})

4、计算

前述有两个操作扩大了除数倒数的值，因此需要进行恢复：

扩展恢复：除以2^{𝑎𝑑𝑑𝑟_𝑏𝑖𝑡+𝑟𝑜𝑚_𝑏𝑖𝑡}

截位恢复：除以2^{𝑀−𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡} ，由于是倒数，截位相当于放大，因此需要除。

 div_tmp=X(被除数 )×rom(addr)/(2^{𝑎𝑑𝑑𝑟_𝑏𝑖𝑡+𝑟𝑜𝑚_𝑏𝑖𝑡} ×2^{𝑀−𝑙𝑒𝑎𝑑𝑖𝑛𝑔_𝑏𝑖𝑡})

div_tmp=X(被除数 )×rom(addr)/2^{𝑀+𝑟𝑜𝑚_𝑏𝑖𝑡−1}

由于设计需要是Q4.8，保留8位小数，因此最终结果为：div_out=div_tmp∗2⁸

 

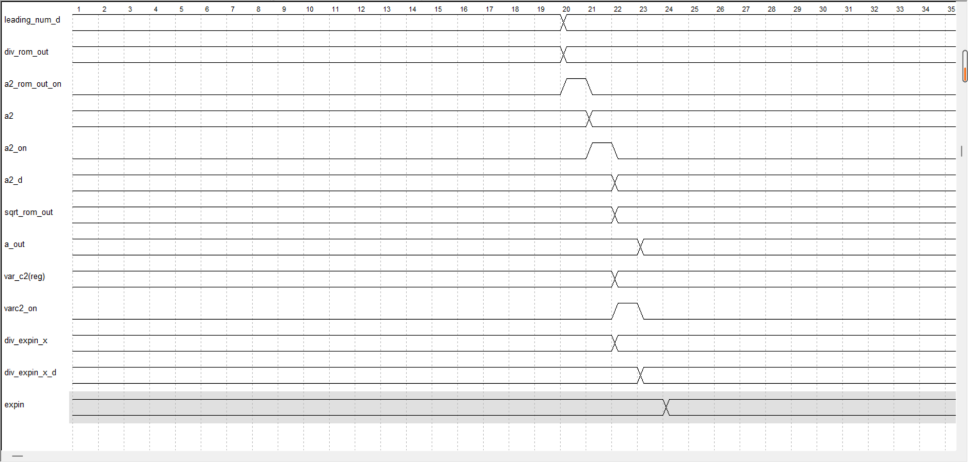
1.2 实现流程

1）确定最高 M位；
2）上述 M位除去最高位 1，剩余位作为地址，进行倒数查表
3）将被除数与查表得到的倒数相乘，实现除法运算；
4）根据需要截位；

1.3 实例

1.3.1 最小值跟踪噪声SNR计算除法

% module name:    div_snr
% Description:     The lookup table divition function.% leading位计算除法
% 最小值跟踪噪声SNR
% 输入：    Q32/Q32
% 输出Q5.8  max 31-2^8

function div_out = div_snr(X,Y)
global fp_sdec fp_sint
%     fp_sdec = 8;
%     fp_sint = 5;

    leading_bit = 6;%查找表leading位
    addr_bit = leading_bit-1;
    rom_bit = 6;%实际ROM少一位，最高位恒为1不用存 
    K = length(X);%子带数
    M = zeros(K,1);
    leading = zeros(K,1);
    rec = zeros(K,1);
    div_tmp = zeros(K,1);

    rom = zeros(2^addr_bit,1);
    for addr = 0:2^addr_bit-1
        %计算值的时候，需要补充恒为1的最高位；
        rom(addr+1) =  floor( 2^(addr_bit + rom_bit)  /  ( addr + 2^addr_bit) );
        if(addr == 0)
            rom(addr+1) = rom(addr+1) - 1;
        end
    end

    for k = 1:K
        %计算非零位数
        if Y(k) ==0
%             div_tmp(k) = 2^(fp_sint+fp_sdec)-1-2^fp_sdec;%当分母为0时，直接输出最大值
            div_tmp(k) = 1;%当分母为0时，直接输出最小值
        else
            M(k) = floor(log2(Y(k)));
        
        %计算leading位并查表
        %若leading位不足addr_div位，在末尾补0，补足10位
        %if M(k) > addr_div
            leading(k) = floor( Y(k)/2^(M(k)-addr_bit) );%截取leading后多余位数，范围2^addr_bit~2^(addr_bit+1)
            
            rec(k) = rom(  leading(k) - 2^addr_bit + 1  );%查表，减去恒为1的最高位，matlab地址从1开始因此加1
            
            div_tmp(k) = floor( X(k)*rec(k)/2^(rom_bit+M(k)-fp_sdec) );%计算除法，并保留8位小数
            
            if(div_tmp(k)>(2^(fp_sint+fp_sdec)-1-2^fp_sdec))%20210729
                div_tmp(k) = 2^(fp_sint+fp_sdec)-1-2^fp_sdec;
            elseif(div_tmp(k) == 0)%输出不能等于，因此特殊处理
                div_tmp(k) = 1;
            end
        end
        
    end
    
        div_out = div_tmp;
    
    
end

1.3.2 维纳增益计算除法

% module name:    div_wiener
% Description:     The lookup table divition function.% leading位计算除法
% 维纳增益计算除法
% 输入：    Q5.8/Q5.8
% 输出：    Q1.8

function div_out = div_wiener(X,Y)

global fp_wdec fp_wint
%     fp_wdec = 8;
%     fp_wint = 1;

    leading_bit = 7;%查找表leading位
    addr_bit = leading_bit-1;
    rom_bit = 9;%实际ROM少一位，最高位恒为1不用存 
    K = length(X);%子带数
    M = zeros(K,1);
    leading = zeros(K,1);
    rec = zeros(K,1);
    div_tmp = zeros(K,1);

    rom = zeros(2^addr_bit,1);
    for addr = 0:2^addr_bit-1
        %计算值的时候，需要补充恒为1的最高位；
        rom(addr+1) =  floor( 2^(addr_bit + rom_bit)  /  ( addr + 2^addr_bit) );
        if(addr == 0)
            rom(addr+1) = rom(addr+1) - 1;
        end
    end

    for k = 1:K
        %计算非零位数
        if Y(k) ==0
             div_tmp(k) = 0;
        else
            M(k) = floor(log2(Y(k)));
        
            %计算leading位并查表
            %若leading位不足addr_div位，在末尾补0，补足10位
            %if M(k) > addr_div
            leading(k) = floor( Y(k)/2^(M(k)-addr_bit) );%截取leading后多余位数，范围2^addr_bit~2^(addr_bit+1)
            
            rec(k) = rom(  leading(k) - 2^addr_bit + 1  );%查表，减去恒为1的最高位，matlab地址从1开始因此加1
            
            div_tmp(k) = floor( X(k)*rec(k)/2^(rom_bit+M(k)-fp_wdec) );%计算除法，并保留8位小数
            
            if(div_tmp(k)>(2^(fp_wint+fp_wdec)-1))%20210729
                div_tmp(k) = 2^(fp_wint+fp_wdec)-1;
            elseif(div_tmp(k) == 0)
                div_tmp(k) = 1;
            end
            
         end
            
     end
    %输出肯定小于1，不需要限幅
    
    div_out = div_tmp;
    
    
end